ЛР3

Цель работы: Знакомство со спектральным представлением периодических и случайных процессов; Изучение взаимосвязи преобразований сигналов во временной и частотной областях; Оценка дефектов дискретного преобразования Фурье и методы их подавления.

Выполнение работы.

Сначала создаем два сигнала: x2=4*cos(2*pi*f2*t) и x1=cos(2*pi*f1*t).

Выбираем частоты f1 и f2 заданные преподавателем.

Временной интервал (базу анализа) выбераем так, дабы более низкочастотный сигнал из имеющихся имел на

интервале 3-5 периодов.

Задаем частоту дискретизации так, чтобы на периоде сигнала высокой частоты укладывалось от 4 до 10 отсчетов.

Получаем модуль спектра сигнала, строим его график.

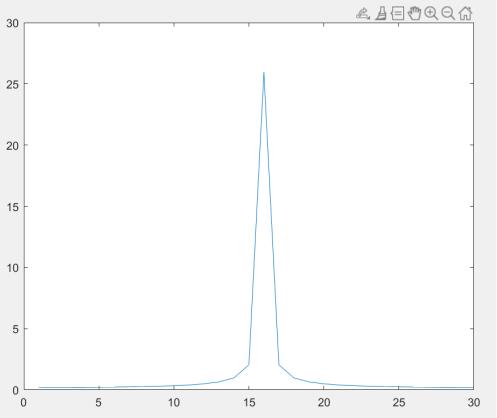
f1 = 0.25; % частота дискретизации, Гц

f2 = 10;

L = 30;

F = 50;

T = 1/F;

t = (0:L-1)*T;

% 1 пункт figure (1)

x1 = cos(2*pi*f1*t);

plot (fftshift(abs(fft(x1))));

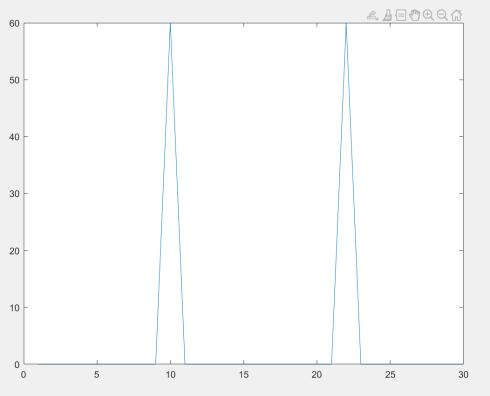
figure (2)

x2 = 4*cos(2*pi*f2*t); plot(fftshift(abs(fft(x2))));

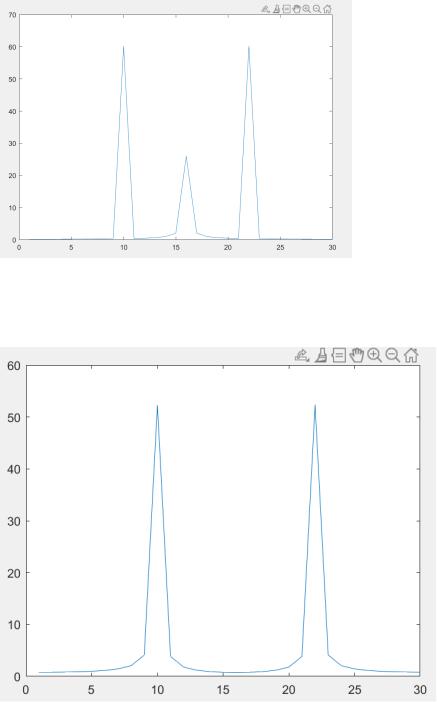
Создаем еще два сигнала: x3=x1+x2; x4=x1.*x2 и строим их спектры.

figure (3) x3=x1+x2;

plot(fftshift(abs(fft(x3))));

figure (4) x4=x1.*x2;

plot(fftshift(abs(fft(x4))));

На временном интервале отсчетов создаем импульс и получаем его спектр (фазу и модуль).

%3 пункт

N=2^7;

T = zeros(1,N); % временной интервал

T(5) = 1;

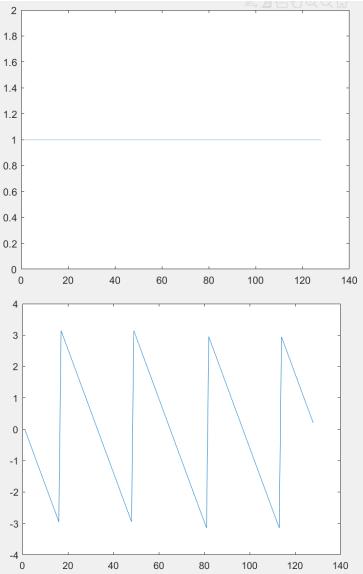
figure (5) plot(abs(fft(T)));

figure (6)

plot(angle(fft(T))); % поменять сигма импульс

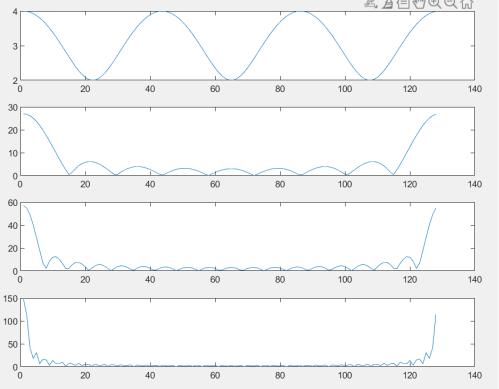
В цикле (for) последовательно увеличиваем ширину нашего импульса, наблюдая при этом соответствующие изменения спектра импульса. Для произвольной ширины импульса рассчитаем его спектр вручную.

%4 пункт figure (7)

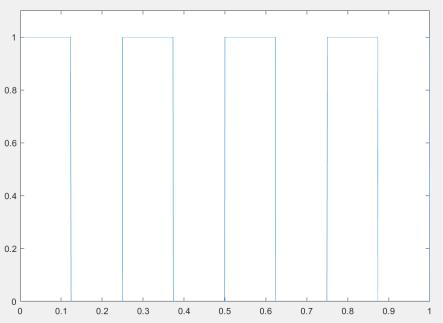
На том же самом временном интервале создаем прямоугольный периодический сигнал со скважностью 2 (меандр) и с количеством периодов, кратным двум. Строим его спектр. Расчет спектра выполняем вручную.

N=2^7;

f=4;

T=1/f;

dt=T/N;

t=0:dt:4*T;

M=square(2*pi*t*f);

figure (8) plot(t,M); axis([0 1 0 1.1]);

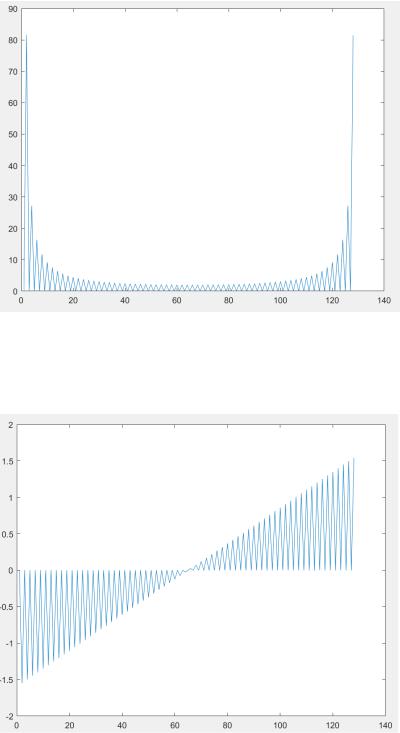
figure (9) plot(abs(fft(M,N)));

figure (10) plot(angle(fft(M,N)));

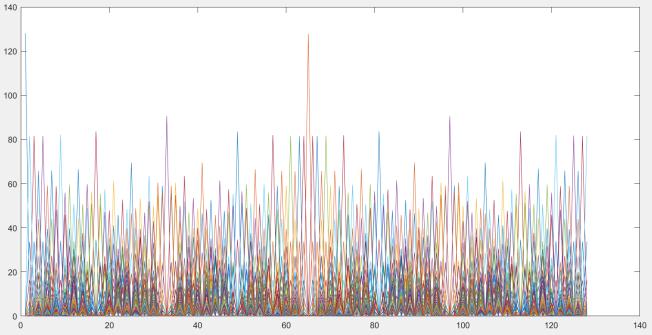
Операцией kron(A,А),создаем базис Уолша. Далее строим спектр того же сигнала. Сравниваем спектры Уолша и Фурье

% 6 пункт

N=2^7;

A=[1,1; 1,-1]; K = kron (A,A);

for i = 1:1:5

K=kron(K,A);

end

figure (11) plot(abs(fft(K)));

Определяем ширину и форму частотной характеристики двух соседних каналов анализатора Фурье.

Это можно сделать в цикле (for), сначала изменяя частоту анализируемого сигнала с весьма малым шагом (0.1 – 0.2), затем выделяя из спектра только отчет, принадлежащий выбранному нами каналу.

Оцениваем, как меняется спектр моногармонического сигнала при его смещении по частотной оси.

Для более качественного анализа используется, окно