Контрольная_2

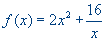1. Н айти минимум функции методом секущих, на интервале [1;5], ɛ=0.1.

Решение

Определяем функцию:

y=@(x) (2*x^2+16/x)

y =

@(x)(2*x^2+16/x)

Производная:

y1=@(x) (4*x-16/x^2)

y1 =

@(x)(4*x-16/x^2)

Границы интервала и точность:

a=1;b=5;eps=0.1;

Алгоритм метода секущих:

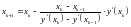
Начальное приближение:

x(1)=a;x(2)=b;

Вводим алгоритм:

k=2;

while abs(x(k)-x(k-1))>eps

x(k+1)=x(k)-(x(k)-x(k-1))/(y1(x(k))-y1(x(k-1)))*y1(x(k));

k=k+1;

end

Результат:

x

x =

1.0000 5.0000 2.5306 0.9264 1.9885 1.7683 1.5475 1.5918

Число итераций:

k-2

ans =

6

Погрешность расчёта:

double(abs(x(k)-x(k-1)))

ans =

0.0443

2. Найти минимум функции методом Ньютона (метод касательных), положив ɛ=0.1, x0=1.

Решение

Алгоритм метода:

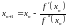
Определяем первую и вторую производные:

y1=@(x) (4*x-16/x^2)

y1 =

@(x)(4*x-16/x^2)

y2=@(x) (4+32/x^3)

y2 =

@(x)(4+32/x^3)

Вводим точность и начальное приближение:

eps=0.1;x(1)=1;

Вводим алгоритм расчёта:

k=1;

while abs(y1(x(k)))>eps x(k+1)=x(k)-y1(x(k))/y2(x(k));k=k+1;end

Число итераций:

k-1

ans =

3

Результат:

x

x =

1.0000 1.3333 1.5429 1.5861

Погрешность расчёта:

abs(x(k)-x(k-1))

ans =

0.0433