500

1.

X	0.4	0.8	1.2	1.6	2	2.4
Y	7	8	8	16	20	29

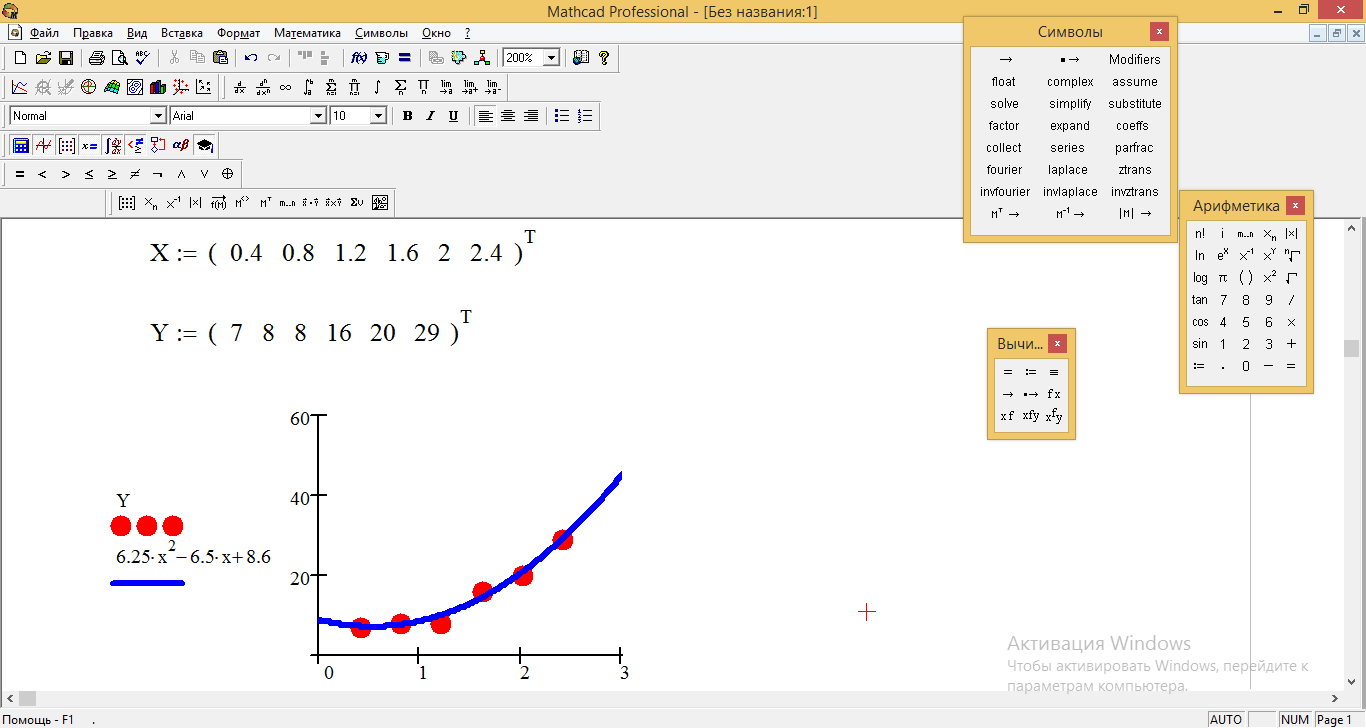
Уравнение регрессии имеет вид y = cx² + bx + a Находим параметры уравнения методом наименьших квадратов. Система уравнений МНК: an + b∑x + c∑x² = ∑y a∑x + b∑x² + c∑x³ = ∑yx a∑x² + b∑x³ + c∑x⁴ = ∑yx²

X	y	x2	y2	x y	x3	x4	x2 y
0.4	7	0.16	49	2.8	0.064	0.0256	1.12
0.8	8	0.64	64	6.4	0.512	0.41	5.12
1.2	8	1.44	64	9.6	1.728	2.074	11.52
1.6	16	2.56	256	25.6	4.096	6.554	40.96
2	20	4	400	40	8	16	80
2.4	29	5.76	841	69.6	13.824	33.178	167.04
8.4	88	14.56	1674	154	28.224	58.24	305.76
1.4	14.667	2.427	279	25.667

Для наших данных система уравнений имеет вид 6a + 8.4b + 14.56c = 88 8.4a + 14.56b + 28.22c = 154 14.56a + 28.22b + 58.24c = 305.76 Получаем c = 6.25, b = -6.5, a = 8.6 Уравнение регрессии: y = 6.25x²-6.5x+8.6

2.

Формула Симпсона основана на замене подынтегральной функции f(x) на отрезке [a, b] дугой параболы, т.е. функция f(x) аппроксимируется параболой вида: P(x)=αx² + βx + γ. Разобъем отрезок [a, b] на четное число равных отрезков n = 2m, при этом точки x₀, x₂, x₄, ... , x_n-2, x_n - точки деления (x₀ = a, x_n = b). Обозначим через x₁, x₃, x₅, ... середины отрезков [x₀, x₂], [x₂, x₄], [x₄, x₆] и т.д. Применив для каждого отрезка разбиения элементарную формулу Симпсона, получим формулу парабол. Формула Симпсона:

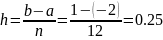
I	xi	yi
0	-2	1.4207
1	-1.75	1.3342
2	-1.5	1.2449
3	-1.25	1.1542
4	-1	1.0655
5	-0.75	0.9865
6	-0.5	0.9316
7	-0.25	0.9255
8	0	1
9	0.25	1.1827
10	0.5	1.4894
11	0.75	1.9318
12	1	2.5277

Остаточный член квадратурной формулы:

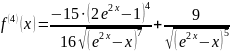
Найдем максимальное значение четвертой производной функции на интервале [-2;1].

Таким образом, I = 3.789 ±

3.

Найдем корни уравнения: x³-3·x²-4·x+3 = 0 ε = 0.0000001 Используем для этого Метод секущих. Если итерации x_n и x_n+1 расположены достаточно близко друг к другу, то производную f’(x_n) в алгоритме Ньютона можно заменить ее приближенным значением: Таким образом, из формулы метода Ньютона получим формулу секущих: Геометрический смысл такого изменения алгоритма Ньютона состоит в том, что от аппроксимации f(x) касательной мы переходим к секущей. Останов: |x_n+1-x_n|< ε, где ε - заданная точность. Метод секущих уступает методу Ньютона в скорости сходимости, однако не требует вычисления производной функции f(x). Находим вторую производную: d²F/dx² = 6•(x-1) Решение. F(3)=-9; F(5)=33 Поскольку F(3) •F(5)<0 (т.е. значения функции на его концах имеют противоположные знаки), то корень лежит в пределах [3;5]. Вычисляем значения функций в точке a = 3. f(3) = -9 f''(3) = 12 Поскольку f(a)•f''(a) < 0, то x₀ = b = 5 Остальные расчеты сведем в таблицу.

N	x	F(x)	h' = (x-xn-1) / (f(x) - f(xn-1))	h = f(x)*h'
1	5	33	0.1818	6

Ответ: x = -1; F(x) = 3

4.

Матричная норма, подчиненная l₁ векторной норме имеет вид

Матричная норма, подчиненная максимальной векторной норме имеет вид

Норма Фробениуса: 

{\displaystyle \|A\|_{F}=\|A\|_{2}={\sqrt {\sum _{i,j}|a_{ij}|^{2}}}={\sqrt {\mathrm {Tr} \,A^{\dagger }A}}}