101 Материальная точка движется прямолинейно. Уравнение движения имеет вид s = 2t + 0,04t3 (расстояние – в метрах, время – в секундах). Найти скорость и ускорение точки в моменты времени t1 = 0 и t2 = 5 с. Каковы средние значения скорости и ускорения за первые 5 с движения?

Скорость движения  - это производная от  пути по времени, то есть v(t)=2+0.12*t^2, Ускорение - производная от скорости по времени a(t)=0.24*t. v(t=0)=2 м/с v(t=5)=5 м/с. a(t=0)=0 м/с^2, a(t=5)=0.24*5=1.2 м/с^2. За 5 секунд тело прошло s=2*5+0.04*5^3=15 м, то есть средняя скорость за 5 секунд составляет Vср=15/5=3 м/с. Ускорение меняется по линейному закону, поэтому среднее возьмём как среднее арифметическое aср=(0+1,2)/2=0,6 м/с^2.

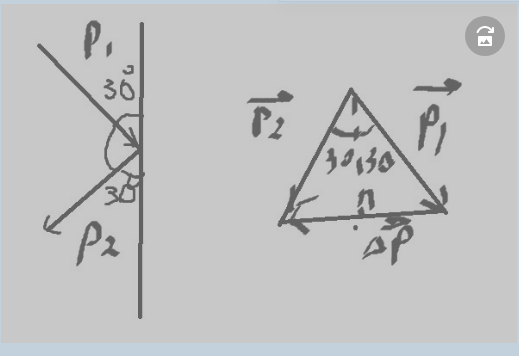
107 Шарик массой 200 г ударился о стенку со скоростью 10 м/с и отскочил от неё с такой же скоростью. Определить импульс, полученный стенкой, если до удара шарик двигался под углом рад 6 π к плоскости стенки. Решим геометрически dp=2mV*sin30=2*0.2*10*0.5=2 кг*м/с

113 Пружина жесткостью 1000 Н/м была сжата на 4 см. Какую нужно совершить работу, чтобы сжатие пружины увеличилось до 18 см? F=k*x

F = 1000 * 0,18 = 180 H

18-4=14 см = 0,14 м

A = 180 * 0,14 = 25,2 Дж

125 Человек стоит на скамейке Жуковского и ловит рукой мяч массой 0,4 кг, летящий в горизонтальном направлении со скоростью 20 м/с. Траектория мяча проходит на расстоянии 0,8 м от вертикальной оси вращения скамейки. С какой угловой скоростью начнет вращаться скамейка Жуковского с человеком, поймавшим мяч? (Считать, что суммарный момент инерции человека и скамейки 6 кг⋅м2.)

131 На каком расстоянии от поверхности Земли напряженность ее гравитационного поля равна 1 Н/кг?

Ну можно предположить так g0 = 9,8 м/с² − ускорение свободного падения у поверхности Земли

R = 6400 км − радиус Земли

g = 1 м/с² − ускорение свободного падения на высоте H над Землёю

===================================================

H − ? высота

Ускорение свободного падения (напряжённость гравитационного поля Земли) определяется из закона всемирного тяготения:

{g0 = G•M/R²

{g = G•M/(R + H)²

где G − гравитационная постоянная,

M − масса Земли

Выразим из уравнений G•M:

G•M = g•(R + H)² = g0•R²

Мы получили выражение теоремы Остроградского-Гаусса: ускорение

свободного падения обратно пропорционально квадрату расстояния

до центра Земли.

Решим уравнение относительно высоты H:

(R + H)/R = 1 + H/R = √(g0/g)

H = R•[√(g0/g) − 1]

Подставим численные значения:

H = 6400•[√(9,8/1) − 1] = 13640 км

Ответ: H = 13640 км 

119 Маховик насажен на горизонтальную ось. На обод маховика намотан шнур, к которому привязан груз массой 800 г. Опускаясь равноускорено, груз прошел 160 см за 2 с. Радиус маховика 20 см. Определить момент инерции маховика Решение. m*g-T=m*a; T*R=J*e; e=a/R; a=(2*S)/(t^2); m*g-(J*e)/R=m*a; m*g-m*a=(J*a)/(R^2); J=(m*(R^2)*(g-a))/a; m=0,8; R=0,1; S=1,6; t=2; g=9,8; М=F*r F=ma=0.8*a S=at2/2 a=2S/t^2=2*1.6/4=0.8 м/с2 M=0.8*0.8*0.1=