
КР1 Дифференциальное исчисление
.docxНайдите
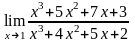 .
.
При
подстановке значения
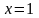 в выражение, стоящее под знаком предела,
неопределенности не возникает. Тогда
получаем:
в выражение, стоящее под знаком предела,
неопределенности не возникает. Тогда
получаем:
 .
.
Найдите
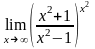 .
.
Используем второй замечательный предел:
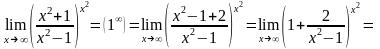
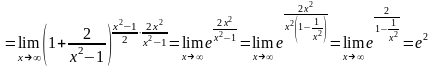 .
.
Проверьте непрерывность функции
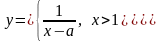 для
для
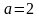 .
Для точек разрыва установите их характер.
При каком
.
Для точек разрыва установите их характер.
При каком
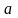 функция будет непрерывной?
функция будет непрерывной?
Для
данная функция имеет вид
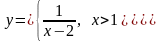 .
Рассмотрим точку
:
.
Рассмотрим точку
:
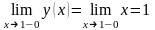 ,
, 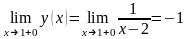 .
.
Отсюда
следует, что точка
является точкой разрыва первого рода.
Скачок функции в данной точке равен
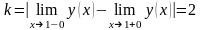 .
Найдем
,
при котором данная функция будет
непрерывной:
.
Найдем
,
при котором данная функция будет
непрерывной:
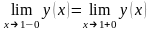 ,
, 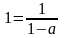 ,
, 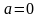 .
.
Найдите производные функций:
а) 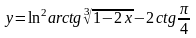 ;
;
б) 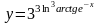 ;
;
в) 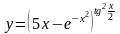 .
.
а) .
Используем правила дифференцирования и таблицу производных:
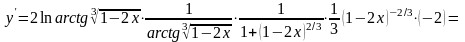
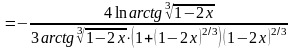 .
.
б) .
Используем правила дифференцирования и таблицу производных:
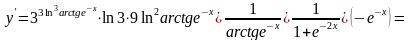
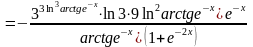 .
.
в) .
Используем логарифмическую производную, правила дифференцирования и таблицу производных:
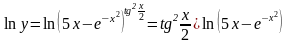 ,
,
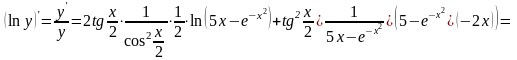
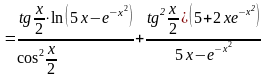 ,
,
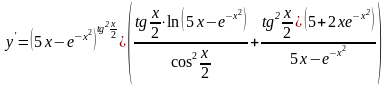 .
.
Вычислите дифференциалы первого и второго порядка для функции
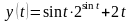 .
.
Найдем производную первого порядка:
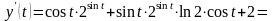
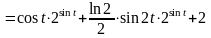 .
.
Найдем производную второго порядка:
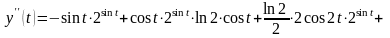
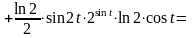
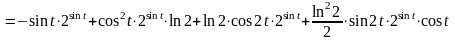 .
.
Тогда получаем:
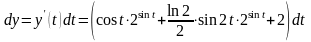 -
дифференциал первого порядка,
-
дифференциал первого порядка,
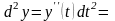
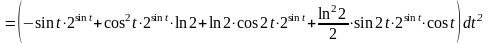 -
дифференциал второго порядка.
-
дифференциал второго порядка.
Проведите исследование функции
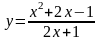 и постройте эскиз ее графика.
и постройте эскиз ее графика.
Область определения функции
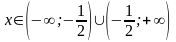 .
.
Рассмотрим
точку
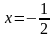 :
:
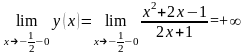 ,
,
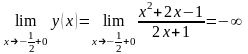 .
.
Отсюда следует, что точка является точкой разрыва второго рода.
Четность и нечетность.
При
замене
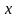 на
на
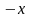 получаем, что
получаем, что
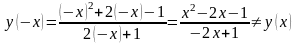 и
и
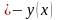 ,
откуда следует, что данная функция не
является ни четной, ни нечетной, то есть
данная функция является функцией общего
вида.
,
откуда следует, что данная функция не
является ни четной, ни нечетной, то есть
данная функция является функцией общего
вида.
Асимптоты и поведение функции на концах области определения.
Вертикальная
асимптота – прямая
.
Ищем наклонные асимптоты вида
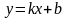 :
:
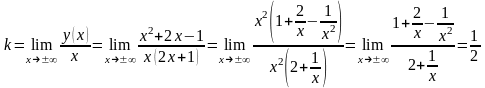 ,
,
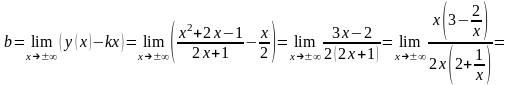
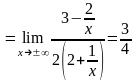 .
.
Отсюда
следует, что есть наклонная асимптота
– прямая
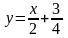 .
Концами области определения являются
.
Концами области определения являются
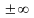 .
Тогда получаем:
.
Тогда получаем:
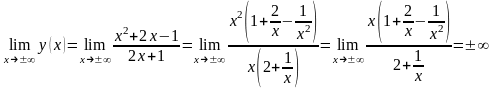 .
.
Пересечение графика функции с осями координат.
Если
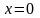 ,
то
,
то
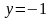 .
Если
.
Если
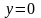 ,
то
,
то
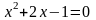 ,
откуда
,
откуда
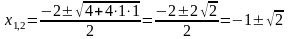 .
Следовательно, график функции пересекает
ось OX в точках с координатами
.
Следовательно, график функции пересекает
ось OX в точках с координатами
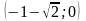 и
и
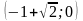 ,
и график функции пересекает ось OY в
точке с координатами
,
и график функции пересекает ось OY в
точке с координатами
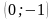 .
.
Возрастание и убывание функции, точки экстремума.
Найдем первую производную данной функции и приравняем ее нулю:
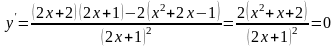 ,
,
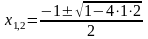 -
нет действительных решений.
-
нет действительных решений.
Отсюда
следует, что точек экстремума нет.
Исследуем знак
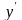 на каждом из интервалов области
определения функции:
на каждом из интервалов области
определения функции:
-
при
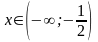
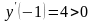 - функция возрастает;
- функция возрастает;
-
при
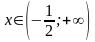
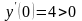 - функция возрастает.
- функция возрастает.
Выпуклость и вогнутость графика функции, точки перегиба.
Найдем вторую производную данной функции и приравняем ее нулю:
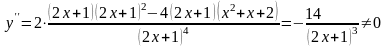 .
.
Отсюда
следует, то точек перегиба нет. Исследуем
знак
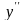 на каждом из интервалов области
определения функции:
на каждом из интервалов области
определения функции:
-
при
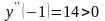 - график функции вогнутый;
- график функции вогнутый;
-
при
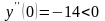 - график функции выпуклый.
- график функции выпуклый.
На основании полученных данных строим график функции:

Найдите полный дифференциал функции
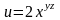 .
.
Найдем частные производные первого порядка:
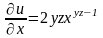 ,
, 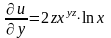 ,
, 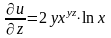 .
.
Тогда полный дифференциал имеет вид:
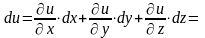
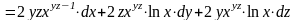 .
.
Проверьте, что функция
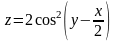 удовлетворяет дифференциальному
уравнению
удовлетворяет дифференциальному
уравнению
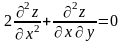 .
.
Найдем
частную производную
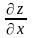 :
:
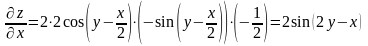 .
.
Найдем
частные производные
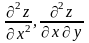 :
:
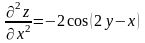 ,
, 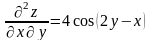 .
.
Тогда получаем:
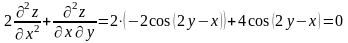 .
.
Следовательно, данная функция удовлетворяет заданному дифференциальному уравнению.
Найти производную функцию
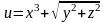 в точке
в точке
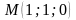 по направлению к точке
по направлению к точке
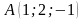 .
.
Найдем частные производные первого порядка и их значения в точке :
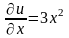 ,
, 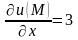 ,
,
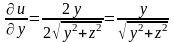 ,
, 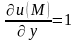 ,
,
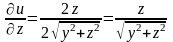 ,
, 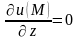 .
.
Из
точки
в точку
направлен вектор
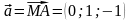 .
Найдем его направляющие векторы:
.
Найдем его направляющие векторы:
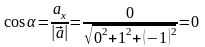 ,
,
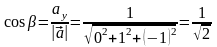 ,
,
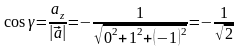 .
.
Тогда искомая производная равна:
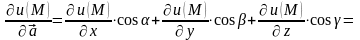
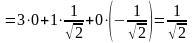 .
.
