Решение КР3 Вар1
.docВекторная алгебра и аналитическая геометрия
1. В плоскости
найти вектор
,
перпендикулярный вектору
и имеющий одинаковую с ним длину.
Решение.
По условию задачи
вектор
лежит в плоскости
,
значит, его координата
,
т.е.вектор имеет координаты
.
Из условия
перпендикулярности векторов
и
следует равенство нулю их скалярного
произведения, т.е.
Найдем длины векторов и :
По условию задачи
длины векторов равны, т.е.
Составим и решим систему уравнений:
Таким образом,
получаем два набора координаты для
вектора
-
и
.
Ответ: , .
2. Компланарны ли
три вектора:
,
,
?
Решение.
Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.
Вычислим смешанное
произведение векторов
в координатной форме:
Смешанное произведение не равно нулю, значит, векторы не компланарны.
Ответ: векторы не компланарны.
3. Даны вершины
треугольника
,
,
.
Составить уравнения: а) трех его сторон;
б) медианы
;
в) высоты
.
Решение.
а) Составим уравнение
стороны
как прямой, проходящей через 2 точки:
Аналогично получаем:
для стороны
:
для стороны
:
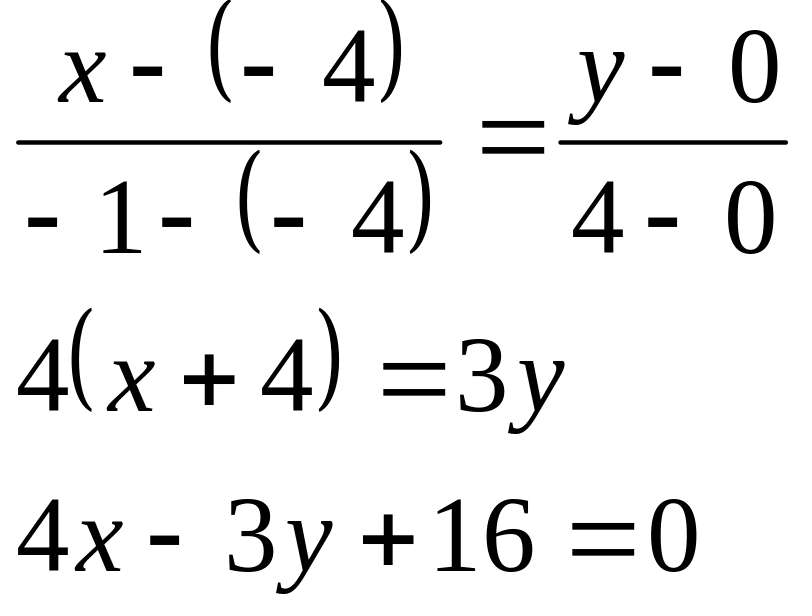
б) Для
составления уравнения медианы
предварительно найдем координаты точки
- середины стороны
:
Получили точку
.
Составим уравнение медианы
как прямой, проходящей через 2 точки:
в) Уравнение
высоты
найдем как уравнение прямой, проходящей
через точку
перпендикулярно прямой
.
Из уравнения прямой
получаем вектор нормали
.
Из условия перпендикулярности следует,
что данный вектор может быть принят в
качестве направляющего вектора прямой
.
Итого, уравнение высоты
составим по точке
и направляющему вектору
:
Ответ: а)
,
,
;
б)
;
в)
.
4. Вычислить угол
между двумя прямыми:
и
Решение.
Если прямые заданы
уравнениями с угловыми коэффициентами
и
,
то тангенс угла между прямыми можно
найти по формуле:
Имеем из уравнения
,
из уравнения
-
Подставляем и получаем:
Ответ:
.
5. Прямая и плоскость
заданы уравнениями
и
.
Какая из перечисленных ситуаций имеет место и почему:
1) прямая лежит в плоскости?
2) прямая параллельна плоскости?
3) прямая пересекает плоскость?
Решение.
Из уравнения прямой
получаем координаты ее направляющего
вектора
и точки, принадлежащей прямой
Из уравнения
плоскости
получаем координаты ее нормального
вектора
.
Найдем скалярное произведение данных векторов:
Из равенства нулю скалярного произведения можно сделать вывод, что прямая параллельна плоскости или лежит в ней.
Подставим координаты точки в уравнение плоскости :
Получено верное тождество, значит, точка лежит в плоскости, а значит, и все остальные точки прямой лежат в данной плоскости. Таким образом, делаем вывод, что имеет место первая ситуация.
Ответ: прямая лежит в плоскости.