Решение КР2 Вар1

Матрицы и определители

1. Методом Гаусса и методом алгебраических дополнений найдите матрицу, обратную к , если .

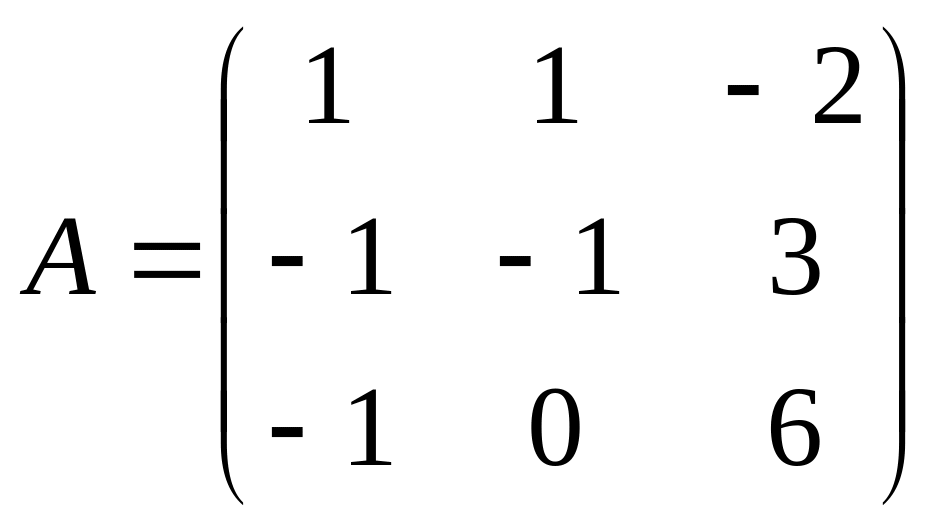Решение.

Найдем обратную матрицу методом методом Гаусса. Для этого запишем матрицу , дописав к ней справа единичную матрицу, и путем элементарных преобразований над строками приведем левую часть полученной матрицы в единичную.

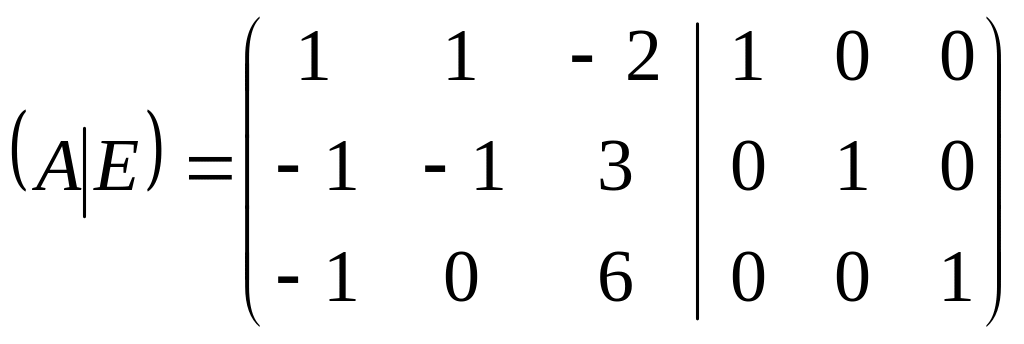
Ко второй строке прибавим первую. К третьей строке прибавим первую:

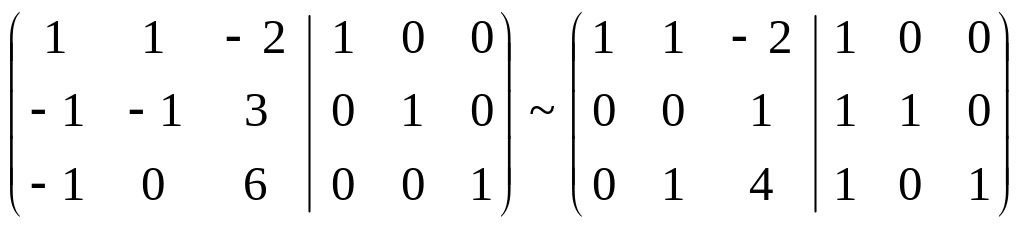
Поменяем местами вторую и третью строки:

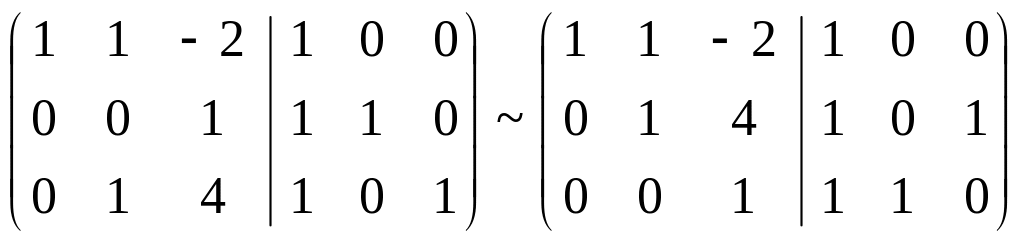
К первой строке прибавим вторую, умноженную на (-1):

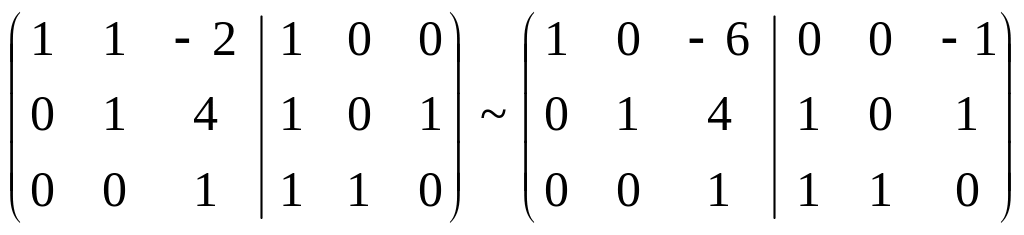
К первой строке прибавим третью, умноженную на 6. Ко второй строке прибавим третью, умноженную на (-4):

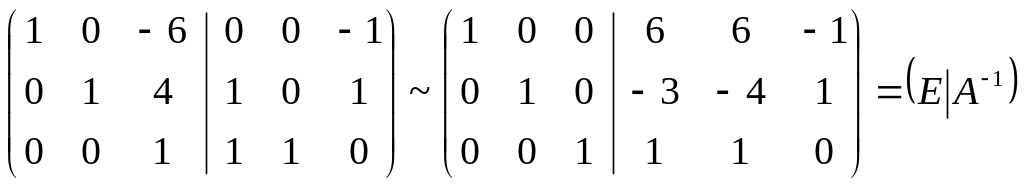
Таким образом, обратная матрица имеет вид:

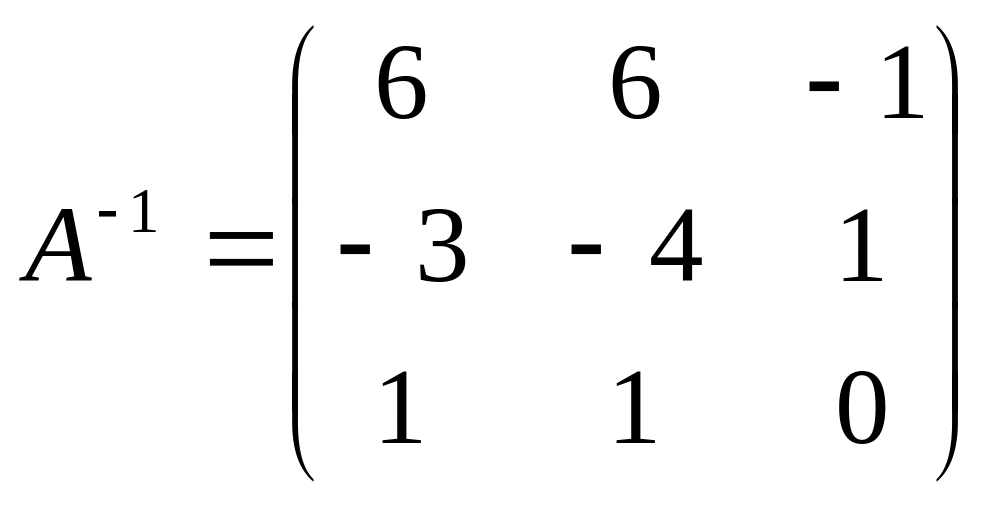
Найдем обратную матрицу методом алгебраических дополнений. Вычислим определитель матрицы :

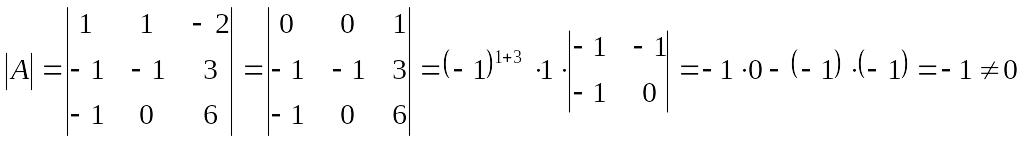
Вычислим алгебраические дополнения элементов исходной матрицы:

,

,

,

,

,

,

,

,

.

Составим матрицу алгебраических дополнений:

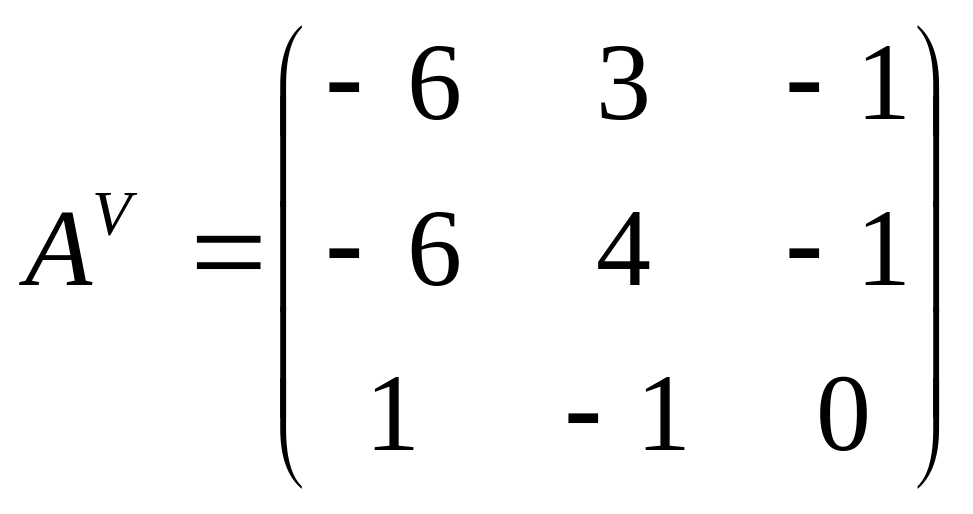
Найдем обратную матрицу по формуле :

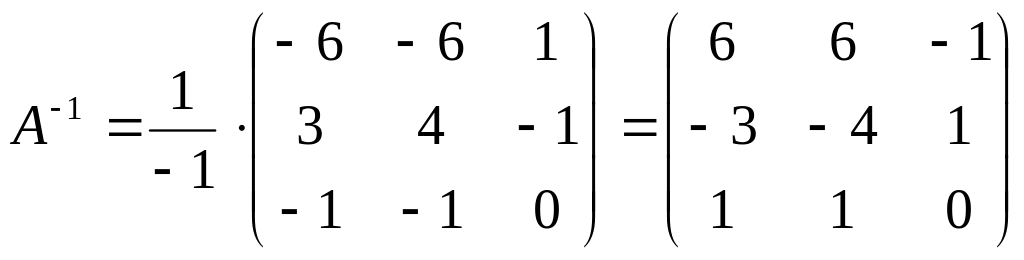
Ответ:

2. Какое из следующих выражений является общим решением системы линейных уравнений и почему:

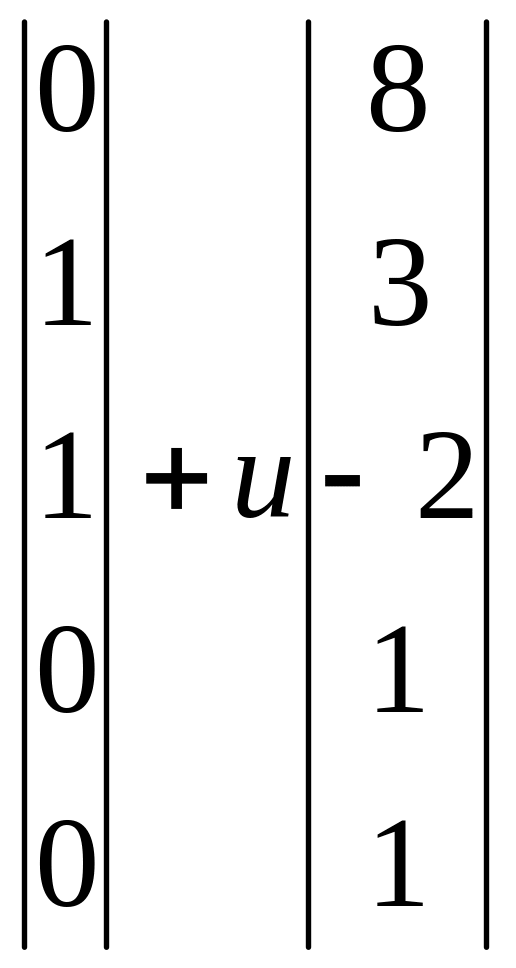1) ; 2) ; 3) 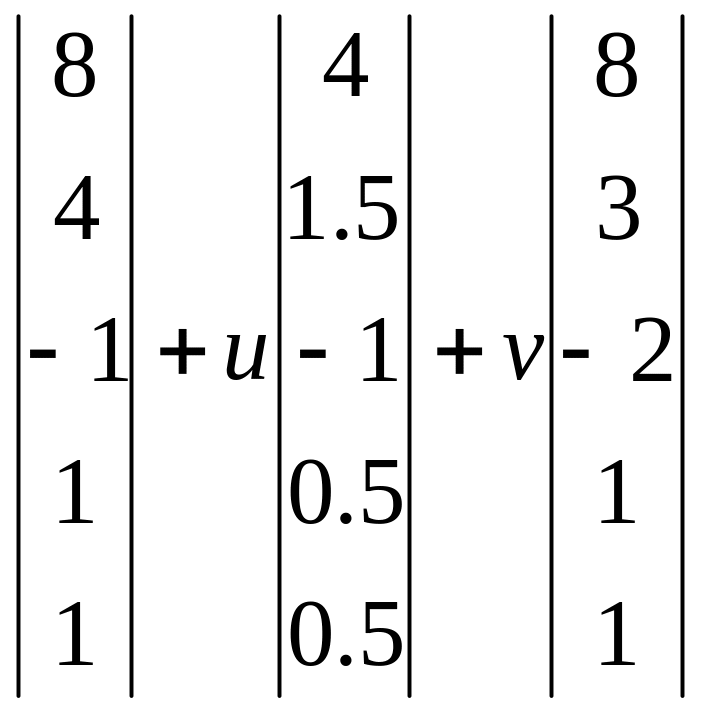; 4) нет решений.

Решение.

Найдем решение системы линейных уравнений методом Жордана-Гаусса. Составим расширенную матрицу коэффициентов системы и приведем ее путем элементарных преобразований над строками к трапециевидному виду:

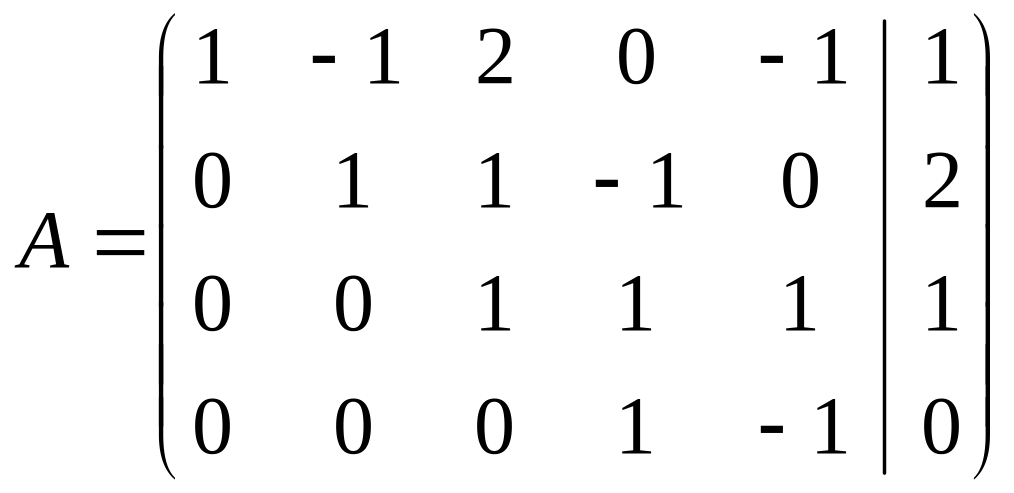
К первой строке прибавим вторую:

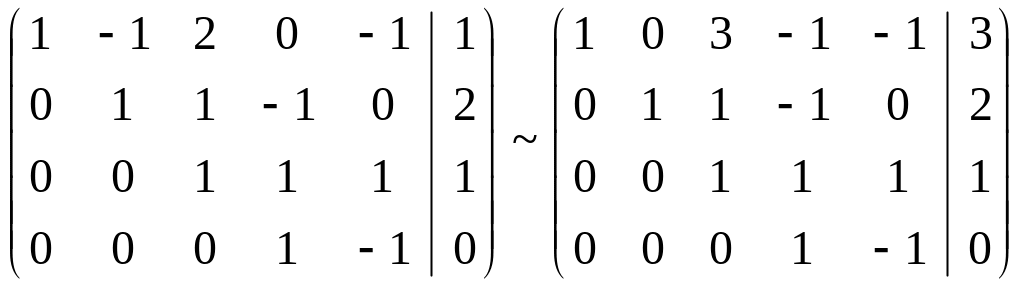
К первой строке прибавим третью, умноженную на (-3). Ко второй строке прибавим третью, умноженную на (-1):

К первой строке прибавим четвертую, умноженную на 4. Ко второй строке прибавим первую, умноженную на 2. К третьей строке прибавим четвертую, умноженную на (-1):

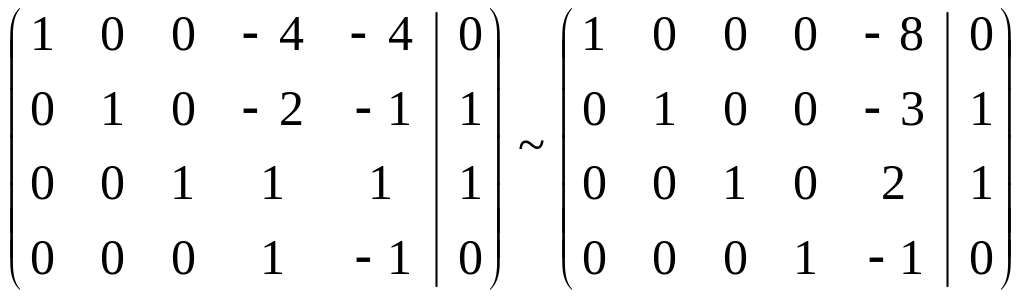
Ранг матрицы коэффициентов равен рангу расширенной матрицы, значит, система совместна. При этом ранг матрицы коэффициентов (4) меньше числа неизвестных (5), поэтому система имеет множество решений.

Четыре неизвестные примем за базисные (т.к. ранг матрицы коэффициентов равен 4), одна неизвестная будет свободной.

Тогда будут базисными переменными, - свободной переменной.

Составим систему уравнений, соответствующую полученной матрице:

Итого, получаем решение:

, , , ,

или в общем виде:

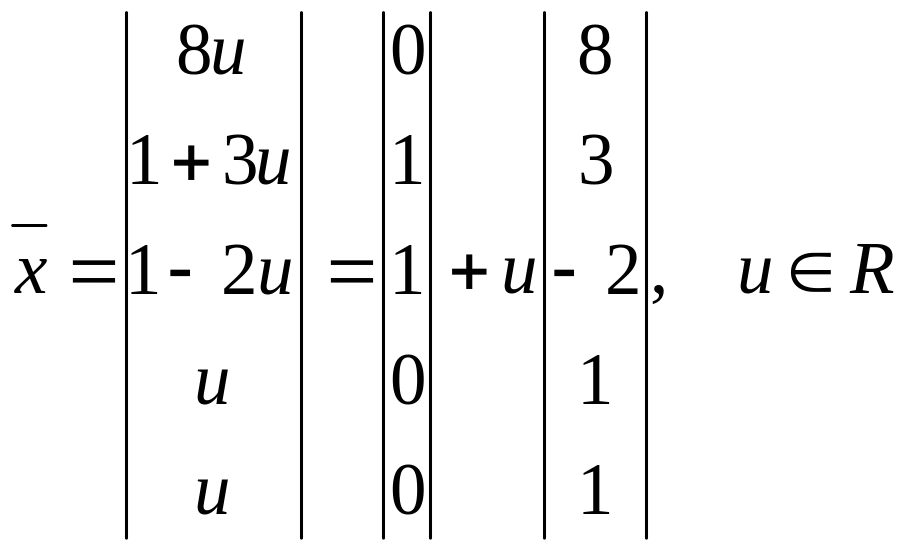
Ответ: 2 вариант -

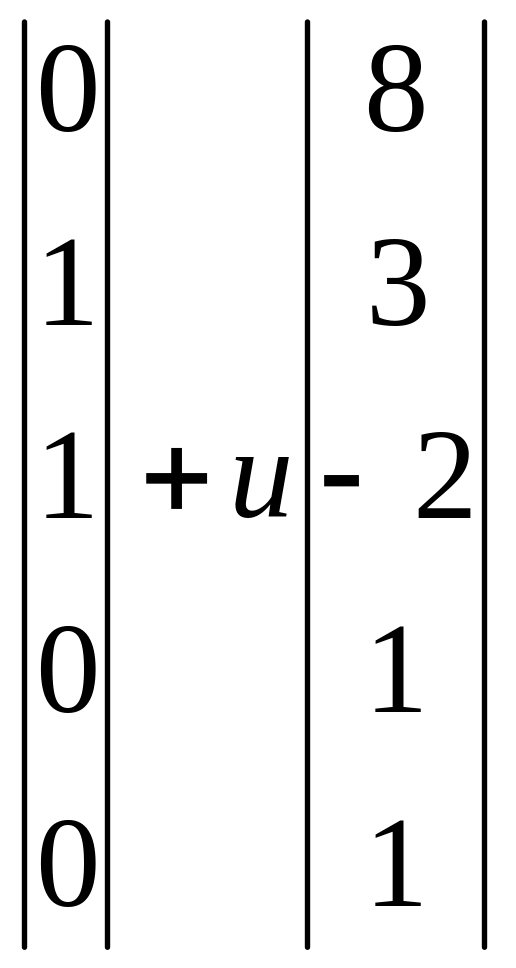
3. Пусть 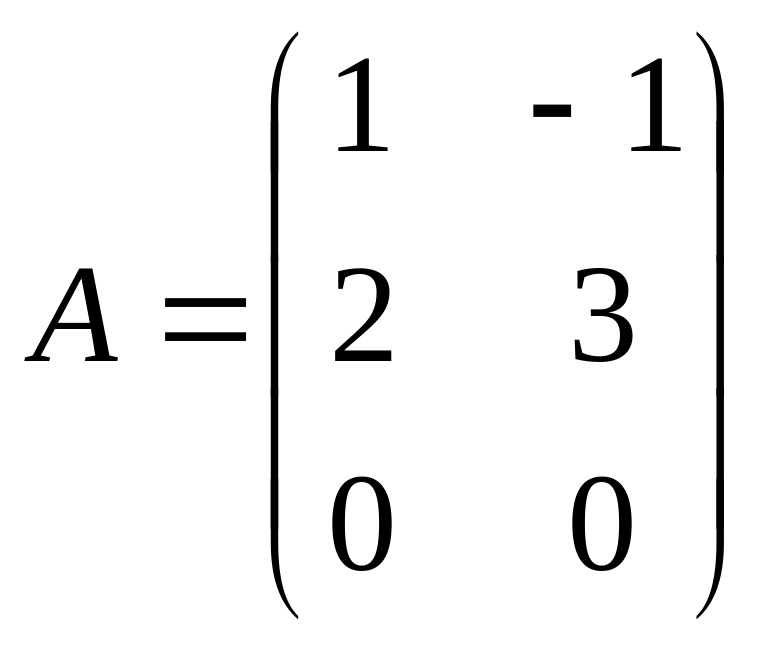, , 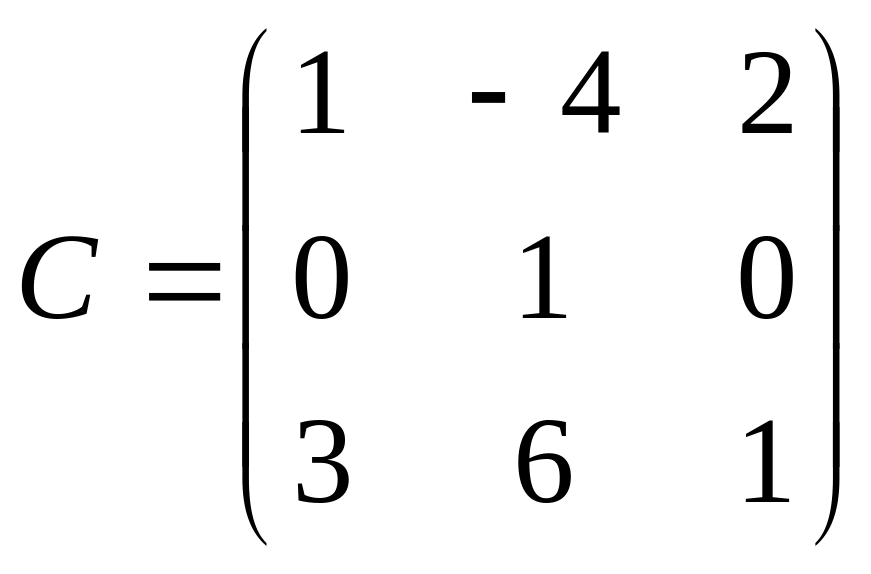. Какое из произведений является матрицей размера ?

1) ; 2) ; 3) ; 4)

Решение.

Две матрицы можно перемножить, если количество столбцов первой матрицы равно количеству строк второй матрицы. Результатом умножения матрицы на матрицу будет матрица .

Имеем матрицы , и .

Произведение является матрицей размерности (произведение является матрицей размерности (т.к. число строк матрицы равно 3, число столбцов равно числу строк , а число столбцов равно 3), соответственно, произведение двух матриц размерности есть матрица размерности ).

Произведение является матрицей размерности (произведение является матрицей размерности (т.к. число строк матрицы равно 2, число столбцов равно числу строк , а число столбцов равно 3), соответственно, произведение есть матрица размерности (т.к. число строк матрицы равно 2, число столбцов равно числу строк , а число столбцов равно 2).

Произведение не существует (потому что не существует произведения - количество столбцов первой матрицы не равно количеству строк второй матрицы).

Произведение является матрицей размерности (рассуждения аналогичны рассуждениям по произведению : произведение является матрицей размерности (т.к. число строк матрицы равно 3, число столбцов равно числу строк , а число столбцов равно 3), соответственно, произведение двух матриц размерности есть матрица размерности ).

Ответ: 2 вариант - является матрицей размерности .

4. Ранг матрицы 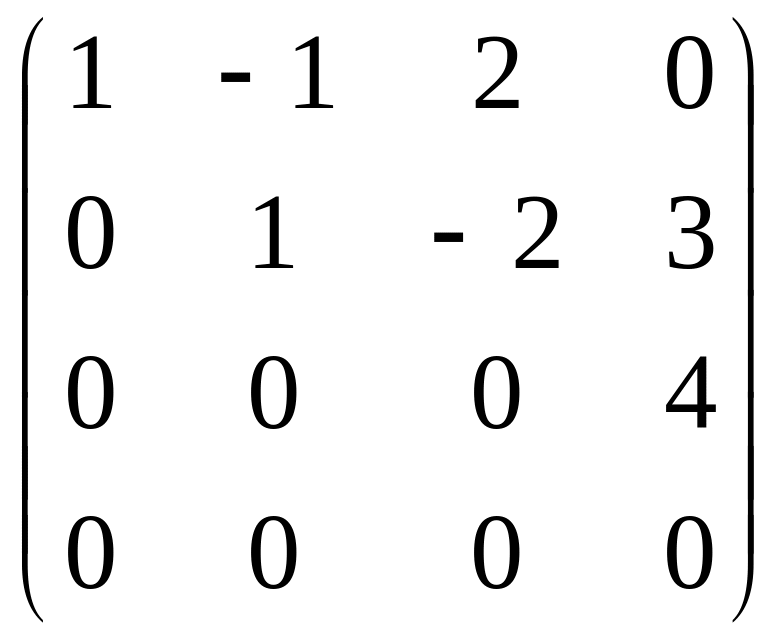равен: 1) 1; 2) 2; 3) 3; 4) 4.

Решение.

Рангом матрицы называется ранг ее системы строк или столбцов, т.е. максимальное количество линейно независимых строк или столбцов этой системы.

Данная матрица уже приведена к ступенчатому виду. Т.к. ненулевых строк 3, то ранг матрицы равен 3.

Ответ: 3 вариант – 3 .