Решение КР1 Вар1

Задача 1.

Выполните действия .

Решение:

Выполним указанные действия:

.

Задача 2.

Найдите решения уравнения . Нарисуйте их на комплексной плоскости.

Решение:

Найдем решения данного уравнения:

,

.

Нарисуем найденные решения на комплексной плоскости:

Задача 3.

Найдите все значения . Ответ запишите в показательной форме.

Решение:

Найдем модуль и аргумент комплексного числа :

, ,

.

Тогда для искомого корня получаем:

, ,

.

б) .

Найдем модуль и аргумент комплексного числа :

, ,

.

Тогда для искомого корня получаем:

, ,

.

Запишем ответ в показательной форме:

.

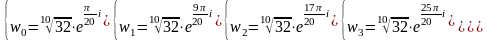Задача 4.

Разложите на множители многочлен .

Решение:

Очевидно, что одним из корней уравнения является . Разделим данный многочлен на :

Корнем уравнения является делитель свободного члена . Разделим полученный многочлен на :

Следовательно, искомое разложение на множители имеет вид .

Задача 5.

Выделите целую часть дроби .

Решение:

Разделим многочлен на многочлен:

Следовательно, , то есть целая часть дроби равна .

Задача 6.

Разложить дробь на простейшие .

Решение:

Представим данную дробь в следующем виде:

.

Используем метод неопределенных коэффициентов:

,

, .

Тогда искомое разложение данной дроби на простейшие имеет вид:

.