Добавил:

KaFaka t.me Инфо для ГУАП студентов от меня: https://kafaka.notion.site/99e6d9b70ca74f7baef3daea17839e5a Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет аэрокосмического приборостроения

Предмет:

Мультимедиа технологии

Файл:

LR3 / мт__МТZлаб03

.pdf

Скачиваний:

Добавлен:

18.06.2024

Размер:

572.14 Кб

Скачать

☆

Лабораторная работа №3.

Изучение методов фильтрации аудиосигналов в MATLAB. Применение рекурсивных фильтров

Цель работы. Получить навыки обработки аудиосигналов на примере методов фильтрации сигналов во временной области с использованием рекурсивных цифровых фильтров.

Краткие теоретические сведения

В лабораторной работе №2 был изучен принцип фильтрации аудиосигналов с использованием фильтрации в спектральном пространстве. Данный метод прост, но требует сравнительно большого объема вычислений, и, кроме того, характеристики фильтра будут неизменными для всей обрабатываемой записи.

Фильтрацию можно производить без вычисления спектра обрабатываемого оцифрованного аудиосигнала, непосредственно во временной области. В частности, уравнение работы рекурсивного цифрового фильтра имеет вид

		q 1		p
y	n	b x	n v		a	r	y	n r	, n 0,1,2,...
	n	v	n v			r		n r
		v 0		r 1

(1)

из которого видно, что формирование массива отсчетов выходного сигнала происходит последовательно. Два массива коэффициентов фильтра ({ar} и {bv}) полностью определяют характеристики фильтра. Заметим, что в системе MATLAB индексация элементов массивов ведется не с нуля, а с единицы, что требует выполнения элементарной модификации всех формул из учебных пособий по обработке сигналов и фильтрации. Впрочем, обычно все стандартные задачи обработки сигналов в MATLAB можно решить вызовом стандартных функций [5], которые не предполагают поэлементную работы с массивами.

Основная задача расчета рекурсивного фильтра заключается в выборе так называемого аналогового фильтра-прототипа некоторого порядка, и вычислении коэффициентов {ar} и {bv} по заданным частотным характеристикам фильтра. Для расчета фильтров существуют разные методы, наиболее простым из которых является метод обобщенного билинейного преобразования передаточной функции аналогового фильтра-прототипа, который и реализован в соответствующих стандартных функциях Matlab.

В листинге 1 приведен текст mat-файла, реализующий алгоритм полосовой фильтрации файла звукового сигнала в диапазоне частот от 200 до 1000 Гц на основе рекурсивного цифрового фильтра (РЦФ), рассчитанного по аналоговому прототипу фильтра семейства Баттерворта 2-го порядка.

Листинг 1 – MATLAB-программа фильтрации аудиосигнала во временной

области посредством РЦФ (пример для реализации полосового фильтра)

clc, clear, close all %очистка памяти [input_signal,Fd] = audioread('D:/input_audio.wav');

N = length(input_signal);%Получить длину данных аудиофайла

IIR_Ord=2; % задаем порядок фильтра-прототипа

%задаем граничные частоты полосы пропускания фильтра low_freq = 200; up_freq = 1000;

%выполняем расчет коэффициентов РЦФ Баттерворта,

%вызывая стандартную функцию butter(...)

[b,a] = butter(IIR_Ord,[2*low_freq./Fd 2*up_freq./Fd],'bandpass');

%осуществляем фильтрацию всей имеющейся записи,

%вызывая стандартную функцию Matlab

output_signal(:,1)=filter(b,a,input_signal(:,1)); output_signal(:,2)=filter(b,a,input_signal(:,2));

%вычисляем спектры входного и выходного сигнала

%только для того, чтобы посмотреть графики изменений,

%внесенных фильтром:

Spectr_input=fft(input_signal(:,1));

Spectr_output=fft(output_signal(:,1));

%строим графики спектров входного и выходного сигналов figure(1)

X=20*log10(abs(Spectr_input)); %Преобразовать в дБ f=[0:(Fd/N):Fd/2]; %Перевести Абсциссу в Гц

X=X(1:length(f));

semilogx(f,X);

grid;

xlabel('Частота (Гц)'); ylabel('Уровень (дБ)');

title('Амплитудные спектры аудиофайлов'); hold on

Y=20*log10(abs(Spectr_output)); %Преобразовать в дБ Y=Y(1:length(f));

hLine(2)=semilogx(f,Y);

figure(1) hold off

legend('input audio','output audio')

%строим график АЧХ фильтра

[H, F] = freqz(b,a, N,'whole',Fd); f=[0:(Fd/N):Fd/2]; W=H(1:length(f));

A_dB = 20*log10(abs(W)

figure(2), semilogx(f, A_dB), grid

% границы вывода по вертикальной оси: MaxA_dB = 20*ceil(max(A_dB)./20);

MinA_dB = 20*floor(min(A_dB)./20);

ylim([MinA_dB MaxA_dB]) xlim([10 22000])

%осуществляем построение графиков

%входного и выходного сигналов figure(3)

subplot(2,1,1); plot(input_signal); subplot(2,1,2); plot(output_signal);

audiowrite('D:/output_audio_filtered.wav', output_signal, Fd)

Если нужно реализовать не полосовой, а любой из трех оставшихся типовых фильтров (фильтр нижних частот, фильтр верхних частот, широкополосный режекторный фильтр) заданного семейства (filter_family), а также изменить параметры фильтра, то в приведенном шаблоне программы необходимо модифицировать значения переменных IIR_Ord, low_freq, up_freq, а также заменить строку, в которой реализуется расчет полосового фильтра

[b,a] = butter(IIR_Ord,[2*low_freq./Fd 2*up_freq./Fd],'bandpass');

на одну из трех строк:

- для расчета ФНЧ частотой среза up_freq:

[b a]=filter_family(IIR_Ord,2 .*up_freq./Fd,'low');

- для расчета ФВЧ с частотой среза low_freq:

[b a]=filter_family(IIR_Ord, 2.*low_freq./Fd,'high');

- для расчета широкополосного режекторного фильтра с частотами среза low_freq и up_freq:

[b a]=filter_family(IIR_Ord,[2.*low_freq./Fd 2.*up_freq./Fd],'stop');

В качестве имени вызываемой функции, обозначенной выше обобщенным именем filter_family (функции с таким названием в Matlab нет), нужно использовать один из следующих вариантов:

-butter – для фильтра семейства Баттерворта,

-cheby1 – для фильтра семейства Чебышева 1-го рода,

-cheby2 – для фильтра семейства Чебышева 2-го рода,

-ellip – эллиптический фильтр.

При вызове функции для расчета фильтра Чебышева нужно дополнительно указывать параметр допустимой неравномерности частотной

характеристики фильтра в пределах полосы пропускания (параметр Rp, от англ. Ripples), выражаемый в децибелах, следующим образом:

[b, a] = cheby1(IIR_Ord, Rp, 2*up_freq./Fd, 'high');

На практике вещественное значение числового параметра Rp выбирают из интервала от 0.1 до 2.

При вызове функции эллиптического фильтра необходимо задавать уже два подобных параметра (Rp и Rs, подробнее см. https://www.mathworks.com/help/signal/ref/ellip.html ).

Необходимо иметь в виду, что при использовании функции cheby2 для реализации режекторного фильтра могут возникать некоторые проблемы.

Заметим, что, если нужно осуществить фильтрацию с не типовыми фильтрами, когда компоненты сигнала в заданном диапазоне частот желательно убрать практически полностью, а, например, когда нужно ослабить сигналы в каком-то частотном диапазоне лишь частично, или даже когда нужно обеспечить усиление в каких-то диапазонах частот, тогда можно формировать выходной сигнал фильтра, смешивая результат фильтрации типовым фильтром и исходный сигнал (до фильтрации), в необходимых пропорциях.

Например, если нужно поднять усиление в области высоких частот в 3 раза, то следует сначала пропустить исходный сигнал (input_signal) через ФВЧ, получив массив аудиосигнала (назовем его output_signal_HP), в котором представлены только компоненты с частотами выше заданной частоты среза, а затем сформировать выходной сигнал фильтра

(output_signal) следующим образом:

output_signal = input_signal + 2.* output_signal_HP;

в результате в выходном сигнале будут представлены все частотные компоненты входного сигнала плюс увеличенные по уровню в 2 раза компоненты с частотами выше заданной: итого, общий уровень компонентов высоких частот окажется больше исходного в 1+2=3 раза, а на остальных частотах компоненты останутся неизменными.

По поводу этого подхода к реализации фильтров следует сделать важное замечание. На частотах, где фильтр ослабляет сигнал, помимо уменьшения амплитуды сигнала происходит и его сдвиг по фазе, и, если сдвиг гармонического сигнала, прошедшего через фильтр, на какой-то частоте окажется близок к 180 градусам, то вместо сложения входного сигнала и сигнала, прошедшего через фильтр, по сути будет происходить частичное вычитание. В результате на частотной характеристике будут заметны “провалы” на частотах, близких к границам заданных полос пропускания полосовых фильтров. Чтобы избежать этого эффекта, при

реализации данного метода следует задавать порядок фильтра-прототипа равным единице (в листинге 1 положить IIR_Ord=1).

Для того, чтобы убедиться, что фильтр, реализованный по методу сложения входного сигнала с одним или несколькими выходными сигналами разных фильтров, можно не только сравнивать графики спектров до и после фильтрации, но и построить амплитудно-частотную характеристику такого фильтра. В листинге 2 приведен фрагмент кода, в котором показан пример получения графика АЧХ.

Листинг 2 – Пример получения графика АЧХ для фильтра, реализованного методом сложения нескольких сигналов

[input_signal,Fd] = audioread(file); N = length(input_signal);

IIR_Ord=1; % для фильтров такого типа задавать первый порядок! % зададим граничные частоты полос пропускания

%двух полосовых фильтров, в Гц: low_f1 = 100;

up_f1 = 250; low_f2 = 1000; up_f2 = 2000;

%коэффициенты двух рекурсивных полосовых фильтров:

[b1,a1]= butter(IIR_Ord, [2*low_f1./Fd, 2*up_f1./Fd], 'bandpass');

[b2,a2]= butter(IIR_Ord, [2*low_f2./Fd, 2*up_f2./Fd], 'bandpass');

%Вычислим АЧХ всего фильтра и построим график:

[H1, F] = freqz(b1,a1, N,'whole',Fd); % перед. ф-я первого ПФ [H2, F] = freqz(b2,a2, N,'whole',Fd); % перед. ф-я второго ПФ

%передаточная функция, тождественно равная 1:

[H0, F] = freqz(1,1, N,'whole',Fd);

%желаемые коэффициенты увеличения уровня в диапазонах:

K1 = 2; K2 = 4;

%комплексная частотная характеристика всего фильтра: H = H0 + (K1-1).*H1 + (K2-1).*H2;

%строим график АЧХ в децибелах:

A_dB = 20*log10(abs(H)); f=[0:(Fd/N):Fd/2]; A_dB=A_dB(1:length(f));

% пределы для графика по вертикали:

MaxA_dB = 20*ceil(max(A_dB)./20); MinA_dB = 20*floor(min(A_dB)./20); figure(2), semilogx(f, A_dB), grid

ylim([MinA_dB MaxA_dB]) % пределы для графика по вертикали xlim([10 22000])

xlabel('Частота, Гц'); ylabel('Уровень, дБ'); title('АЧХ фильтра');

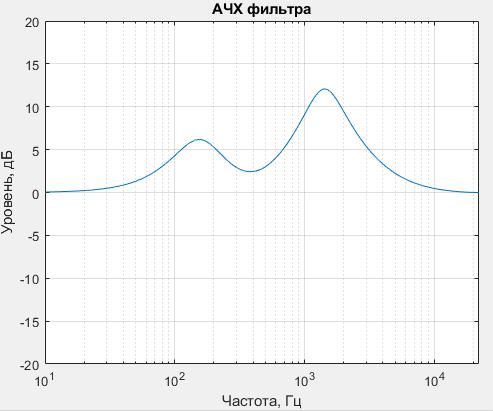
На рисунке 1 приведен результат работы программы, текст которой приведен в листинге 1.

Рисунок 1 – Амплитудно-частотная характеристика фильтра, реализованного в программе, приведенной в листинге 2.

Из анализа рисунка 1 видно, что переход данный фильтр действительно осуществляет поднятие уровня сигнала в двух разных частотных диапазонах (на 6дБ и на 12дБ, т.е. в 2 и в 4 раза соответственно), однако из-за минимального порядка фильтра подъем АЧХ распространяется и на другие частотные диапазоны, хотя и в меньшей степени. Именно по этой причине изменения в характере звука после фильтрации часто будут заметно отличаться от изменений, возникающих при реализации метода фурьефильтрации при тех же настройках частотных параметров фильтра.

Помимо описанных ранее фильтров, существует особый класс избирательных фильтров, которые называются узкополосными: для них отношение центральной частоты полосы пропускания к полосе пропускания много больше единицы. Для реализации узкополосных полосовых цифровых фильтров в MatLAB существует специализированная функция bandpass(...), которая вызывается следующим образом:

output_signal = bandpass(input_signal, [low_freq up_freq], Fd);

От универсальной функции фильтрации она отличается тем, что не требует задания порядка фильтра (константа IIR_Ord в программе,

приведенной на листинге 1), обеспечивая минимально-достаточное значение порядка фильтра для решения большинства практических задач фильтрации аудиосигналов, однако ее использование как элемента для построения цифровых эквалайзеров не рекомендуется из-за вносимых фазовых сдвигов, не позволяющих обеспечить желаемую частотную характеристику.

Варианты заданий

Задание на лабораторную работу предполагает выполнение той же последовательности действий, что была в лабораторной работе №2, отличаться должен только способ программной реализации фильтра: в данной работе следует реализовать рекурсивный фильтр с теми же параметрами, что и в предыдущей работе. Следует осуществить фильтрацию тех же сигналов, что и в лабораторной работе №2 с целью проведения сравнительного анализа двух способов фильтрации аудиосигналов. Семейство аналогового фильтра-прототипа (butter, cheby1, cheby2 или ellip) обучающийся задает по своему усмотрению.

Порядок выполнения работы

1.Согласовать с преподавателем вариант задания во время занятия по расписанию, удостовериться в правильном понимании задания и критериев его оценки.

2.Написать MATLAB-программу, которая реализует метод фильтрации на основе рекурсивного цифрового фильтра и выполнить ту же последовательность действий, что и в лабораторной работе №2.

3.Сравнить звучание аудиозаписей, полученных при выполнении данной и предыдущей лабораторной работы. Акцентировать внимание на различиях, проанализировать свойства полученной частотной характеристики, сформулировать выводы.

4.При желании обучающийся может попробовать реализовать алгоритм фильтрации, используя поотсчетную обработку исходного массива аудиоданных, запрограммировав в цикле формулу (1). Также дополнительно можно попытаться осуществить плавное изменение значений коэффициентов фильтра с тем, чтобы реализовать эффект плавного изменения акустических свойств полученного аудиосигнала в процессе воспроизведения.

Содержание отчета

1.Цель работы.

2.Краткие теоретические сведения о задачах обработки аудиосигналов и их практическом применении, а также о методах фильтрации.

3.Программа с необходимыми комментариями (назначение констант и переменных, функций, и т.п.).

4.Полученные графики: частотной характеристики фильтра, спектров входного и выходного сигнала фильтра с соответствующими подрисуночными подписями.

5.Описание результатов слухового восприятия аудиосигнала после фильтрации и сравнение с результатами, полученными при выполнении лабораторной работы №2.

6.Выводы, в которых отражены особенности изученных методов и свойства полученных результатов.

7.Список используемых источников, желательно не только из списка рекомендуемой литературы, приветствуется использование Интернетресурсов; на все источники в тексте отчета должны быть ссылки.

Контрольные вопросы

1.В чем отличие частотных характеристик фильтров Баттерворта и Чебышева 1-го и 2-го рода?

2.Почему результаты фильтрации с использованием рекурсивного фильтра могут отличаться от результатов, полученных посредством фурье-фильтрации при одинаково заданных параметрах фильтрации?

3.Как выбор значения порядка аналогового фильтра-прототипа влияет на частотную характеристику фильтра?

4.Как можно реализовать фильтр, чтобы он подавлял бы сигнал в нескольких частотных диапазонах?

Рекомендуемая литература

1.Обработка звука – фильтры. / Дмитрий Михайлов

//URL: http://websound.ru/articles/theory/filter.htm

2.Разработка программы для анализа звуковых файлов пакете MATLAB.

//URL: https://gigabaza.ru/doc/106583.html

3.Алгоритм цифровой фильтрации в частотной и временной областях.

//URL: http://stu.sernam.ru/book_g_rts.php?id=137

4.Дьяконов В. MATLAB 8.0 (R2012b): создание, обработка и фильтрация сигналов, Signal Processing Toolbox. // Компоненты и технологии, 2013. №11, с. 151-161

Соседние файлы в папке LR3

#
18.06.202478.47 Кб0output_audio_filtered_high_pass.wav
#
18.06.2024441.04 Кб0output_audio_filtered_high_pass1.wav
#
18.06.2024882.04 Кб0output_audio_filtered_high_pass2.wav
#
18.06.2024327.02 Кб2Z9411_КафкаРС_ММТ_ЛР3.docx
#
18.06.2024438.04 Кб0Z9411_КафкаРС_ММТ_ЛР3.pdf
#
18.06.2024572.14 Кб0мт__МТZлаб03.pdf