ЛР2 / Шифрование_методом_квадрата

Шифр Плейфера (метод квадрата)

Несмотря на то, что этот шифр был разработан Чарльзом Уитстоном, он стал известен как шифр Плейфера. Первое описание шифра Плейфера зарегистрировано в 1854 году. Этот шифр использовался в тактических целях британскими вооруженными силами во Второй англо-бурской войне, а также и в американской армии в Первой мировой войне. Шифр Плейфера очень прост в применении и не требует специального оборудования. С точки зрения объема имеющейся в нем секретной ключевой информации, шифр Плейфера ничем не отличается от шифра простой замены, в частности, от квадрата Полибия (можно использовать ту же самую таблицу замены). Однако шифрование в данном случае выполняется уже не посимвольно (как в квадрате Полибия), а биграммами – последовательно шифруются пары символов открытого сообщения. Это обстоятельство позволило необычайно простым способом резко повысить криптостойкость шифра по сравнению с шифром одноалфавитной замены (квадрат Полибия и другие).

Пусть ключевая таблица шифрования для русского языка имеет размер 6×5. В ней отсутствуют буквы Ё, Й, Ъ, что, тем не менее, никак не влияет на однозначность расшифрования сообщения.

В	С	Е	Ф	Р	А
Н	Ц	У	З	Ы	Л
Ю	Б	Я	Т	Д	О
М	И	К	Г	Ж	П
Х	Ч	Ш	Щ	Ь	Э

Отметим, что для удобства использования секретного ключа данная таблица замены была заполнена с помощью легко запоминающейся фразы-лозунга (не содержащего повторяющихся букв). Использование легко запоминающегося (неочевидного для потенциального противника, а ещё лучше и совершенно бессмысленного по своей сути) «лозунга» позволяет нигде его не записывать, а также не хранить в открытом виде и весь ключ к шифру. После лозунга последовательно записаны все недостающие буквы русского алфавита. Заметим, что как сам лозунг, так и недостающие символы алфавита открытого сообщения в таблицу можно занести в произвольном порядке.

Шифрование биграммами придает шифру Плейфера важное практическое свойство: существенно возрастает криптостойкость шифра. Это связано с тем, что начинает работать рассеивание (при условии, что символы биграммы не находятся в одной строке, либо в одном столбце), поскольку теперь результат шифрования первого символа биграммы открытого сообщения напрямую зависит от того, каков второй (соседний с ним) символ биграммы. В этом случае оба символа шифруемой биграммы в ключевой таблице можно считать вершинами прямоугольника. В качестве замены для каждого символа биграммы берется противоположная ему вершина воображаемого прямоугольника (например, вдоль строки таблицы). Тогда биграмма ЕО превращается в биграмму АЯ (см. таблицу ниже), однако биграмма ЕД превращается уже в биграмму РЯ, а биграмма ЕП превращается в биграмму АК. Во всех трех этих примерах буква Е в результате шифрования получает совершенно разное представление.

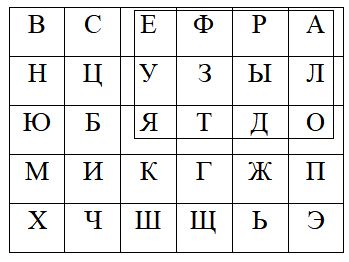
Поэтому частотный крипоанализ зашифрованного сообщения уже не даст желаемого результата, как это было в случае шифра одноалфавитной замены.

Однако, если биграмма открытого сообщения находится в одной строке, либо в одном столбце, то в качестве замены для каждого символа биграммы будет взят символ, находящийся справа (рядом) по строке, либо ниже по столбцу. В этом случае шифрование по сути выполняется так же, как и для шифра одноалфавитной замены «квадрат Полибия» (рассеяния здесь уже нет). Поэтому шифр Плейфера в известной степени является некоторой «своеобразной комбинацией» шифров одноалфавитной и многоалфавитной замены.

Если символ является последним в столбце, то он циклически заменяется на первый символ этого же столбца. Сказанное в равной мере касается и строк таблицы. Например, биграмма НУ перейдет в биграмму ЦЗ, а биграмма СИ - в биграмму ЦЧ. Если биграмма содержит одинаковые символы, то, очевидно, что и зашифрованы они будут одинаково. Например, биграмма НН превратится в биграмму ЦЦ. Всё это является определенным недостатком шифра Плейфера. Расшифрование принятого сообщения выполняется в обратном порядке. Взлом шифра Плейфера осуществляется с помощью частотного анализа повторяемости биграмм в тексте. Эти осредненные зависимости также давно рассчитаны и являются устойчивыми характеристиками для всех естественных языков. Однако возможных биграмм в тексте во много раз больше, нежели букв в алфавите любого естественного языка. Взлом такого шифра - более сложная задача по сравнению со взломом шифра одноалфавитной замены.

Шифрование методом двойного квадрата

Шифр двойного квадрата (двойной квадрат Уитстона) является дальнейшим развитием/усовершенствованием шифра Плейфера. Шифр успешно использовался германскими вооруженными силами уже во Второй мировой войне. В нем шифрование производится одновременно по двум секретным ключевым таблицам.

Например:

В	С	Е	Ф	Р	А
Н	Ц	У	З	Ы	Л
Ю	Б	Я	Т	Д	О
М	И	К	Г	Ж	П
Х	Ч	Ш	Щ	Ь	Э

Х	Ч	Ш	Э	Ю	Я
Д	Ж	З	К	П	Ф
С	О	Л	Ь	Б	В
Ц	Ы	И	Щ	У	Т
Г	Е	Р	М	А	Н

Общие принципы шифрования по методу двойного квадрата - те же, что и в шифре Плейфера, но вдвое увеличивается объем секретной ключевой информации, а шифрование при этом производится одновременно по двум таблицам. При шифровании один (левый) символ биграммы располагается в левой таблице, а правый символ - в правой таблице. Поэтому прямоугольник для шифрования биграмм строится одновременно по двум таблицам. Соответственно, и символы замены для биграмм берутся из разных таблиц. Например, биграмма ЕТ заменяется биграммой ЯК:

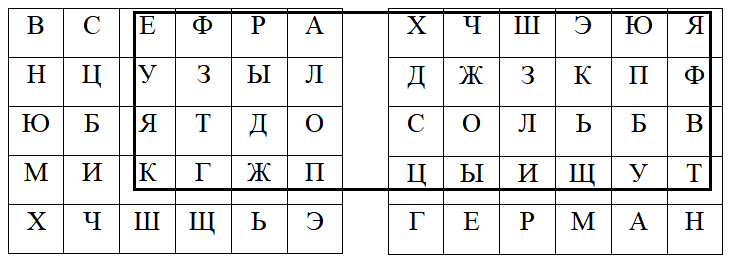
При использовании данного шифра возможна ситуация, когда биграмма открытого сообщения окажется в одной строке для обеих таблиц. В этом случае в криптограмму вместо первой буквы биграммы открытого сообщения записывается буква, находящаяся в том же столбце и в той же строке второй таблицы. Вместо второй буквы биграммы в криптограмму записывается буква, находящаяся в том же столбце той же строки первой таблицы. Так, при шифровании биграммы ХА открытого сообщения в криптограмму записывается биграмма ГЬ.

Использование для шифрования двух таблиц устраняет недостаток шифра Плейфера: биграмма, содержащая одинаковые символы, зашифровывается разными символами. Например, биграмма НН в результате шифрования переходит в биграмму ФХ. При заполнении ключевых таблиц надо следить за тем, чтобы на одноименных позициях в них не находились одни и те же символы (так как это приведёт к ослаблению шифра).