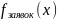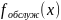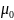Z9411_КафкаРС_ИМ_ПР

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

КАФЕДРА 41

ОЦЕНКА

ПРЕПОДАВАТЕЛЬ

старший преподаватель				М. Н. Шелест
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ПРАКТИЧЕСКОЙ РАБОТЕ №1

МОДЕЛИРОВАНИЕ ЭЛЕМЕНТАРНОЙ СМО С БЕСКОНЕЧНЫМ БУФЕРОМ

по дисциплине: Имитационное моделирование

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	Z9411				Р. С. Кафка
	номер группы		подпись, дата		инициалы, фамилия
Студенческий билет №	2019/3603

Шифр ИНДО

Санкт-Петербург 2024

Цель работы: Нахождение экспериментальной зависимости 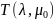для элементарной системы массового обслуживания с бесконечным буфером.

Индивидуальный вариант:

Исходные данные по варианту представлены в таблице 1.

Таблица 1 – Вариант задания

№ варианта	Закон распределения входного потока заявок	Закон распределения времени обслуживания заявок
8	Эрланговский 4 порядка	равномерный	3

Ход работы:

1. Формулы и графики законов распределения вероятностей для интервалов между заявками и времени обслуживания заявок.

Правило поступления потока заявок в систему:

где

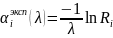
Графики законов распределения вероятностей представлены на рисунках 1-2.

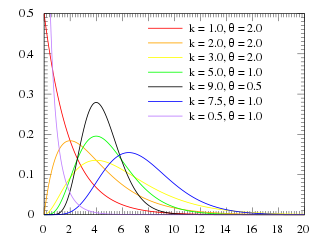Рисунок 1 – Плотность вероятности

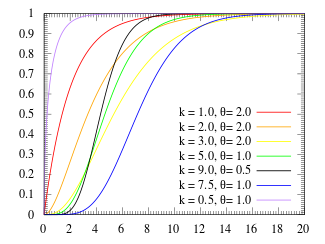Рисунок 2 – Функция распределения

Распределение времени обслуживания заявок:

,

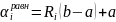где Ri – случайное число в диапазоне [0,1]

График равномерного распределения вероятностей закона распределения времени обслуживания заявок 𝑓обслуж(𝑥) для времени обслуживания заявок представлен на рисунке 3.

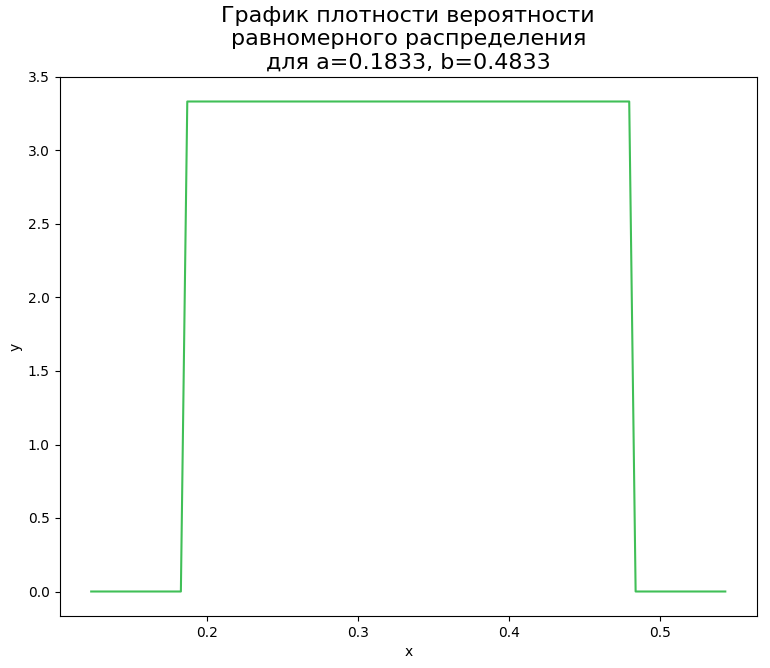Рисунок 3 – График закона распределения вероятностей для времени обслуживания заявок

2. Описание разработанной программы: список использованных переменных, список использованных функций, листинг.

Полный код программы представлен в приложении А.

Список использованных переменных функции modeling_experimental_dependence() для моделирования СМО и построения графиков представлен в таблице 2.

Таблица 2 – Список используемых переменных функции modeling_experimental_dependence()

Название переменной	Описание
shape	Порядок эрлановского распределения заданный вариантом
mu_0	Интенсивностью обслуживания заданная вариантом
is_test	Статус тестовый или экспериментальный запуск программы
lambd	Список значений интенсивности входного потока
a	Левая граница равномерного распределения
b	Правая граница равномерного распределения
t_empirical	Список рассчитанного эмпирически среднего времени обслуживания заявки
l	Итератор по значениям списка интенсивности входного потока lambd
Nu	Теоретически рассчитанный коэффициент вариации обработки
Rho	Теоретически рассчитанный коэффициент загрузки системы
L	Теоретически рассчитанное среднее число заявок в системе
t_theor	Теоретически рассчитанное среднее время обслуживания заявки

Для моделирования смо и построения графиков написали функцию modeling_experimental_dependence(), код функции представлен в листинге 1.

Листинг 1 – Функция построения графиков для модели СМО

def modeling_experimental_dependence(shape, mu_0, is_test = False): '''Функция построения графиков для модели СМО''' # Генерация списка значений интенсивности входного потока lambd = np.linspace(0.1,1,10) * mu_0 # Расчет границ для равномерного распределения a = 1 / mu_0 - 0.05 * mu_0 b = a + 0.1 * mu_0 # Список среднего времени пребывания запроса t_empirical = np.array([]) # Заполнение списка значений среднего времени пребывания запроса for l in lambd: t_empirical = np.append(t_empirical, model(shape, l, a, b, is_test)) print('t_empirical', t_empirical) # Построение графика if is_test: # Построение графика эрланговского распределения # для закона распределения входного потока заявок ploting_erlang_distribution(k=shape, lmbda=1/(np.mean(lambd)*shape), N=10000) # Построение графика равномерного распределения # для закона распределения времени обслуживания заявок ploting_uniform_distribution(a=a, b=b) # Расчет теоритических значений # Расчет теор. значения коэффициента вариации обработки (равномерного распределения) Nu = np.sqrt(((b-a)**2) / 12) / ((a+b) / 2) # Расчет теор. значения коэффициента загрузки системы Rho = lambd[lambd != mu_0]/mu_0 # Расчет теор. значения среднего числа запросов в системе L = (Rho**2 * (1 + Nu**2)) / (2 * (1-Rho)) + Rho # Расчет теор. значения среднего времени пребывания запроса в системе t_theor = L / lambd[lambd != mu_0] # Построение графика георитически расчитанного значения plt.plot(lambd[:len(t_theor)], t_theor, label='Теоретическое значение', color='red') # Построение графика экспериментально полученного значения plt.plot(lambd[:9], t_empirical[:9], label='Рассчитанное значение', color='black') plt.title("График зависимость среднего времени пребывания запроса\nот интенсивности входного потока") plt.ylabel('Ср. t в системе') plt.xlabel('Инт. входного потока') plt.grid() plt.legend() plt.show() return t_empirical

Список использованных переменных функции model() моделирования работы СМО представлен в таблице 3.

Таблица 3 – Список используемых переменных функции model()

Название переменной	Описание
shape	Порядок эрлановского распределения заданный вариантом
mu_0	Интенсивностью обслуживания заданная вариантом
is_test	Статус тестовый или экспериментальный запуск программы
lambd	Список значений интенсивности входного потока
a	Левая граница равномерного распределения
b	Правая граница равномерного распределения
get_t_request	Лямбда ф-ция получения случайного значения распределения для закона распределения входного потока заявок
get_t_work	Лямбда ф-ция получения случайного значения распределения для закона распределения времени обслуживания заявок
n	Количество заявок, поступивших к данному моменту в СМО
k	Количество заявок, обслуженных к данному моменту в ОУ
m	Количество заявок в буфере
is_busy	Статус занятости ОУ (True, если ОУ занят, и False, если ОУ свободен)
t_system	Системное время
t_request	Следующий момент поступления заявки
t_work	Следующий момент освобождения ОУ
t_request_Data	Список времени моментов поступления заявок
t_work_Data	Список времени моментов освобождения ОУ
t_me_Old	Старая оценка среднего времени пребывания запроса
loop_cnt	Счетчик итераций цикла
t_me_New	Текущая на момент расчета оценка среднего времени пребывания запроса

Код функции model() моделирующей работу СМО представлен в листинге 2.

Листинг 2 – Функция моделироваиня СМО

def model(shape, lambd, a, b, is_test): '''Функция моделироваиня СМО''' # Лямбда ф-ция получения случайного значения распределения # Эрланговского для закона распределения входного потока заявок get_t_request = lambda : np.random.exponential(1/lambd) if is_test \ else st.erlang.rvs(a=shape, scale=1/(lambd*shape)) # Равномерного для закона распределения времени обслуживания заявок get_t_work = lambda : np.random.uniform(a, b) # Количество заявок, поступивших / обслуженных / в буфере к данному моменту в СМО n, k, m = 0, 0, 0 # Статус занятости ОУ is_busy = False # Системное время t_system = 0 # Следующий момент поступления заявки t_request = get_t_request() # Следующий момент освобождения ОУ t_work = t_request # Список времени моментов поступления заявок t_request_Data = np.array([]) # Список времени моментов освобождения ОУ t_work_Data = np.array([]) # Старая оценка среднего времени пребывания запроса t_me_Old = 2 ** 32 # Счетчик итераций цикла loop_cnt = 0 # Моделируем СМО while True: loop_cnt += 1 # Увеличиваем счетчик цикла # Проверяем наступило ли время освобождения ОУ if t_request <= t_work: # Записываем в системное время момент поступления заявки t_system = t_request n += 1 # Увеличиваем счетчик поступивших заявок # Сохраняем в список момент поступления заявки t_request_Data = np.append(t_request_Data, t_system) # Проверяем занято ли ОУ if not is_busy: is_busy = True # Устанавливаем статус ОУ в положение занято # Вычисляем следующий момент освобождения ОУ t_work = t_system + get_t_work() else: m += 1 # Добавлием заявку в буфер # Вычисляем следующий момент поступления заявки t_request = t_system + get_t_request() else: # Записываем в системное время момент освобождения ОУ t_system = t_work k += 1 # Увеличиваем счетчик обслуженных заявок # Сохраняем в список момент освобождения ОУ t_work_Data = np.append(t_work_Data, t_system) # Проверяем есть ли заявки в буфере if m > 0: m -= 1 # Берем заявку из буфера # Вычисляем следующий момент освобождения ОУ t_work = t_system + get_t_work() else: # Устанавливаем статус ОУ в положение свободно is_busy = False # Устанавливаем следующий момент освобождения ОУ t_work = t_request # Проводим отценку каждые 1000 итераций цикла if loop_cnt % 1000 == 0: # Высчитываем среднее время обслуживания заявки t_me_New = np.mean(t_work_Data - t_request_Data[:len(t_work_Data)]) # Проверка достаточности условия выхода if (np.abs((t_me_New - t_me_Old)/t_me_Old)) < 0.01: return t_me_New t_me_Old = t_me_New # Перезаписываем среднее время обслуживания заявки

3. Теоретический и экспериментальный графики зависимости среднего времени пребывания заявки в системе от интенсивности входного потока для тестового примера представлен на рисунке 4.

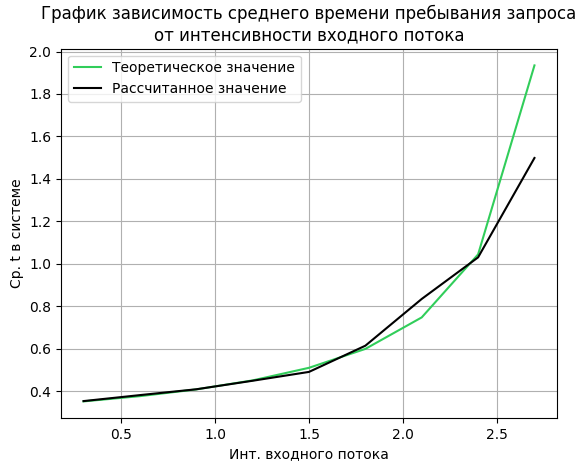Рисунок 4 – График зависимости λ от T для тестового Пуассоновского входного потока

Провёл моделирование для получения требуемой экспериментальнойзависимости при λ = 0.1*µ0, 0.2*µ0, …, 1*µ0. Полученные данные внёс в таблицу 4.

Таблица 4 - Зависимость среднего времени пребывания запроса от интенсивности входного потока

Параметр	Значение
λ	0.3	0.6	0.9	1.2	1.5	1.8	2.1	2.4	2.7	3
T	0.33	0.335	0.337	0.337	0.35	0.362	0.39	0.467	0.668	20.34

График зависимости λ от T для тестового Эрланговского 5 порядка входного потока и равномерного распределения закона обслуживания заявок представлен на рисунке 5.

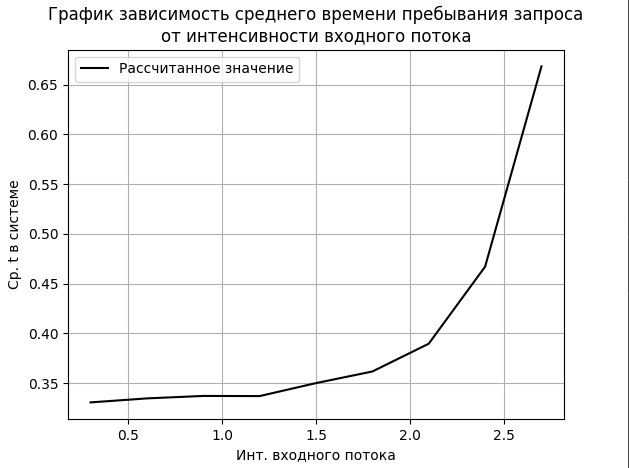Рисунок 5 – График зависимости λ от T для тестового Пуассоновского входного потока

ВЫВОД

В результате практической работы удалось найти экспериментальную зависимость для элементарной системы массового обслуживания (ЭСМО) с бесконечным буфером. В соответствии с вариантом задания была составлена и отлажена моделирующая программа. Для тестового примера было проведено моделирование, а программа была отлажена на тестовом примере. Объем моделирования N был подобран таким образом, чтобы относительная погрешность экспериментальных данных для тестового примера не превосходила 10%. Далее было проведено моделирование для получения требуемой экспериментальной зависимости T(λ,μ0).

В ходе моделирования был реализован эрланговский закон распределения 4 порядка для входного потока заявок и равномерный закон распределения времени обслуживания заявок. Разработанная программа моделировала случайное время появления заявок и время их обслуживания. В зависимости от параметров времени и заполненности буфера она принимала решения об обработках заявок, а мы фиксировали время поступления и обслуживания заявок, по которым потом определяли среднее время нахождения заявки в системе. Расчет средних значений позволил нам построить график зависимости среднего времени пребывания запроса от интенсивности входного потока. Расчеты были проведены при разных значениях интенсивности в диапазоне значений λ = 0.1µ0, 0.2µ0, …, 1µ0, поэтому на графике явно видно, что чем больше интенсивность тем больше среднее время обслуживания. Полученный результат согласуется с нашими представлениями об ЭСМО с постоянным входным потоком и временем обслуживания заявок.

ПРИЛОЖЕНИЕ А. Код программы

from matplotlib import pyplot as plt

from scipy import stats as st

import numpy as np

def ploting_erlang_distribution(k, lmbda, N=10000):

'''Построение графика плотности вероятности Эрланговского распределения'''

# Определяем границы построения графика

data = st.erlang.rvs(a=k, scale=1/lmbda, size=N)

x_min, x_max = min(data), max(data)

# Генерируем список значений x для построения графика

x = np.linspace(0 if x_min<=1 else x_min-1, x_max+1, 100)

# Функция плотности вероятности эрланговского распределения для заданных k и lambda

f = lambda x : ((lmbda**k) * (x**(k-1)) * np.exp(-lmbda*x)) / np.math.factorial(k-1)

# Построение графика

plt.figure(figsize=(9,7))

plt.plot(x, f(x), color='red')

plt.title('График плотности вероятности\nЭрланговского распределения\n' + \

'для k={}, lambda={}'.format(round(k, 4), round(lmbda, 4)), fontsize=16)

plt.xlabel("x")

plt.ylabel("y")

plt.show()

def ploting_uniform_distribution(a, b):

'''Построение графика плотности вероятности равномерного распределения'''

# Генерируем список значений x для построения графика

x = np.linspace(a - (b-a)/5, b + (b-a)/5, 100)

# Функция плотности вероятности равномерного распределения для заданных a и b

f = lambda x : [1/(b-a) if (a<=i) and (i<=b) else 0 for i in x]

# Построение графика

plt.figure(figsize=(9,7))

plt.plot(x, f(x), color='red')

plt.title('График плотности вероятности\nравномерного распределения\n' + \

'для a={}, b={}'.format(round(a, 4), round(b, 4)), fontsize=16)

plt.xlabel("x")

plt.ylabel("y")

plt.show()

def model(shape, lambd, a, b, is_test):

'''Функция моделироваиня СМО'''

# Лямбда ф-ция получения случайного значения распределения

# Эрланговского для закона распределения входного потока заявок

get_t_request = lambda : np.random.exponential(1/lambd) if is_test \

else st.erlang.rvs(a=shape, scale=1/(lambd*shape))

# Равномерного для закона распределения времени обслуживания заявок

get_t_work = lambda : np.random.uniform(a, b)

# Количество заявок, поступивших / обслуженных / в буфере к данному моменту в СМО

n, k, m = 0, 0, 0

# Статус занятости ОУ

is_busy = False

# Системное время

t_system = 0

# Следующий момент поступления заявки

t_request = get_t_request()

# Следующий момент освобождения ОУ

t_work = t_request

# Список времени моментов поступления заявок

t_request_Data = np.array([])

# Список времени моментов освобождения ОУ

t_work_Data = np.array([])

# Старая оценка среднего времени пребывания запроса

t_me_Old = 2 ** 32

# Счетчик итераций цикла

loop_cnt = 0

# Моделируем СМО

while True:

loop_cnt += 1 # Увеличиваем счетчик цикла

# Проверяем наступило ли время освобождения ОУ

if t_request <= t_work:

# Записываем в системное время момент поступления заявки

t_system = t_request

n += 1 # Увеличиваем счетчик поступивших заявок

# Сохраняем в список момент поступления заявки

t_request_Data = np.append(t_request_Data, t_system)

# Проверяем занято ли ОУ

if not is_busy:

is_busy = True # Устанавливаем статус ОУ в положение занято

# Вычисляем следующий момент освобождения ОУ

t_work = t_system + get_t_work()

else:

m += 1 # Добавлием заявку в буфер

# Вычисляем следующий момент поступления заявки

t_request = t_system + get_t_request()

else:

# Записываем в системное время момент освобождения ОУ

t_system = t_work

k += 1 # Увеличиваем счетчик обслуженных заявок

# Сохраняем в список момент освобождения ОУ

t_work_Data = np.append(t_work_Data, t_system)

# Проверяем есть ли заявки в буфере

if m > 0:

m -= 1 # Берем заявку из буфера

# Вычисляем следующий момент освобождения ОУ

t_work = t_system + get_t_work()

else:

# Устанавливаем статус ОУ в положение свободно

is_busy = False

# Устанавливаем следующий момент освобождения ОУ

t_work = t_request

# Проводим отценку каждые 1000 итераций цикла

if loop_cnt % 1000 == 0:

# Высчитываем среднее время обслуживания заявки

t_me_New = np.mean(t_work_Data - t_request_Data[:len(t_work_Data)])

# Проверка достаточности условия выхода

if (np.abs((t_me_New - t_me_Old)/t_me_Old)) < 0.01: return t_me_New

t_me_Old = t_me_New # Перезаписываем среднее время обслуживания заявки

def modeling_experimental_dependence(shape, mu_0, is_test = False):

'''Функция построения графиков для модели СМО'''

# Генерация списка значений интенсивности входного потока

lambd = np.linspace(0.1,1,10) * mu_0

# Расчет границ для равномерного распределения

a = 1 / mu_0 - 0.05 * mu_0

b = a + 0.1 * mu_0

# Список среднего времени пребывания запроса

t_empirical = np.array([])

# Заполнение списка значений среднего времени пребывания запроса

for l in lambd:

t_empirical = np.append(t_empirical, model(shape, l, a, b, is_test))

print('t_empirical', t_empirical)

# Построение графика

if is_test:

# Построение графика эрланговского распределения

# для закона распределения входного потока заявок

ploting_erlang_distribution(k=shape, lmbda=1/(np.mean(lambd)*shape), N=10000)

# Построение графика равномерного распределения

# для закона распределения времени обслуживания заявок

ploting_uniform_distribution(a=a, b=b)

# Расчет теоритических значений

# Расчет теор. значения коэффициента вариации обработки (равномерного распределения)

Nu = np.sqrt(((b-a)**2) / 12) / ((a+b) / 2)

# Расчет теор. значения коэффициента загрузки системы

Rho = lambd[lambd != mu_0]/mu_0

# Расчет теор. значения среднего числа запросов в системе

L = (Rho**2 * (1 + Nu**2)) / (2 * (1-Rho)) + Rho

# Расчет теор. значения среднего времени пребывания запроса в системе

t_theor = L / lambd[lambd != mu_0]

# Построение графика георитически расчитанного значения

plt.plot(lambd[:len(t_theor)], t_theor, label='Теоретическое значение', color='red')

# Построение графика экспериментально полученного значения

plt.plot(lambd[:9], t_empirical[:9], label='Рассчитанное значение', color='black')