Z9411_КафкаРС_ИМ_ЛР1

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

КАФЕДРА 41

ОЦЕНКА

ПРЕПОДАВАТЕЛЬ

старший преподаватель				М. Н. Шелест
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1

МОДЕЛИРОВАНИЕ ВХОДНОГО ПОТОКА ЗАПРОСОВ

по дисциплине: Имитационное моделирование

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	Z9411				Р. С. Кафка
	номер группы		подпись, дата		инициалы, фамилия
Студенческий билет №	2019/3603

Шифр ИНДО

Санкт-Петербург 2024

Цель работы: Исследование основных характеристик входных потоков заявок, а также базовых принципов моделирования СМО по событиям.

Индивидуальный вариант:

Вариант №8: Порядок эрланговского потока – 4; параметр  – 8.

Ход работы:

1. Расчёт теоретического значения интенсивности  и вариации v_u:

Оценку интенсивности вычислил по формуле:

Формула для показателя вариации:

Нормальное распределение описывается следующей формулой:

График эрлановского распределения показан на рисунке 1.

Рисунок 1 – График Эрлановского распределения

2. Описание разработанной программы: список использованных переменных, список использованных функций, блок-схема, листинг.

Основная блок-схема программы представлена на рисунке 2. Каждая функция будет представлена и описана в виде отдельного блока ниже. Полный код представлен в приложении А в конце лабораторной работы.

Рисунок 2 – Основная блок-схема кода

1. Функция main().

Главная функция, которая вызывает другие функции для построения графиков и моделирования Эрланговского распределения.

Список использованных переменных представлен в таблице 1. Программный код функции представлен в листинге 1, блок-схема представлена на рисунке 3.

Таблица 1 – Список используемых переменных функции main()

Название переменной	Описание
k	Порядок эрланговского потока
lamda	Параметр потока λ

Листинг 1 – Функция main()

def main(): k, lmbda = 4, 8 ploting_erlang_distribution(k, lmbda, N=10000) erlang_model(k, lmbda, N=1) return 0

Рисунок 3 – Блок-схема функции main()

2. Функция ploting_erlang_distribution(k, lmbda, data = [], N=10000, iner_cnt = 50, add_hist=False)

Функция строит график плотности Эрланговского распределения и, при необходимости, гистограмму.

Список использованных переменных представлен в таблице 2. Программный код функции представлен в листинге 2.

Таблица 2 – Список используемых переменных функции ploting_erlang_distribution

Название переменной	Описание
k	Порядок эрланговского потока
lamda	Параметр потока λ
data	Список чисел для построения гистограммы. Если список пуст, генерируются новые данные.
N	Количество случайных чисел для генерации, если data пуст
iner_cnt	Количество интервалов для гистограммы.
add_hist	Флаг, указывающий, следует ли добавить гистограмму на график.
weights	Веса столбцов гистограммы.
intervals, entries, x_min, x_max, delta	Результаты функции slicearray
f	Функция плотности вероятности Эрланговского распределения.
x	Список значений x для построения графика.

Листинг 2 – Функция ploting_erlang_distribution

def ploting_erlang_distribution(k, lmbda, data = [], N=10000, iner_cnt = 50, add_hist=False): '''Построение графика плотности Эрланговского распределения''' plt.figure(figsize=(9,7)) # Проверка переданны ли дынные для построения гистограммы if not data: data = random_erlang_val(k, lmbda, N) else: N = len(data) # Определение интервалов и их длительности, min/max значений для построения гистограммы intervals, entries, x_min, x_max, delta = slicearray(data, iner_cnt) # Проверка добавлять гистограмму или нет if add_hist: # Подсчет весов столбцов гистограммы weights = [cnt / (N * delta) for cnt in entries] plt.hist(intervals[:-1], intervals, weights = weights, label='Рассчитанное значение') # Функция плотности вероятности эрланговского распределения для заданных k и lambda f = lambda x : ((lmbda**k) * (x**(k-1)) * np.exp(-lmbda*x)) / np.math.factorial(k-1) # Генерируем список значений x для построения графика x = np.linspace(0 if x_min<=1 else x_min-1, x_max+1, 100) plt.plot(x, f(x), label='График плотности вероятности\nЭрланговского распределения\nдля k={}, lambda={}'.format(k, lmbda), color='red') plt.title("График плотности вероятности\nЭрланговского распределения", fontsize=16) plt.xlabel("x") plt.ylabel("y") plt.legend() plt.show()

Описание функции ploting_erlang_distribution:

1. Начало функции

2. Проверка, переданы ли данные для построения гистограммы (условие if not data)

3. Определение интервалов и их длительности, min/max значений для построения гистограммы

4. Проверка, добавлять гистограмму или нет (условие if add_hist)

5. Определение функции плотности вероятности эрланговского распределения для заданных k и lambda

6. Генерация списка значений x для построения графика

7. Построение графика

8. Конец функции

3. Функция random_erlang_val(k, lmbda, N=10000)

Функция генерирует список из N случайных чисел, распределенных по закону Эрланга.

Список использованных переменных представлен в таблице 3. Программный код функции представлен в листинге 3.

Таблица 3 – Список используемых переменных функции random_erlang_val

Название переменной	Описание
k	Параметр формы для Эрланговского распределения.
lamda	Параметр масштаба для Эрланговского распределения.
N	Количество случайных чисел для генерации.
f	Вспомогательная функция для генерации случайного числа, распределенного по закону Эрланга.

Листинг 3 – Функция random_erlang_val

def random_erlang_val(k, lmbda, N=10000): '''Функция создающая случайное число распределенное по закону Эрланговского распределения''' f = lambda : -1/lmbda * sum(np.log(np.random.uniform(0,1)) for i in range(k)) return [f() for n in range(N)]

Описание функции random_erlang_val:

1. Начало функции

2. Определение вложенной функции f, которая генерирует случайное число, распределенное по закону Эрланга

3. Возвращение списка из N чисел, сгенерированных функцией f

4. Конец функции

4. Функция slicearray(array, intervals_cnt = 10)

Функция разбивает список на интервалы и подсчитывает количество попаданий в каждый интервал.

Список использованных переменных представлен в таблице 4. Программный код функции представлен в листинге 4.

Таблица 4 – Список используемых переменных функции slicearray

Название переменной	Описание
array	Список чисел для разбиения на интервалы.
intervals_cnt	Количество интервалов для разбиения списка.
interval	Список интервалов.
entries	Список количества попаданий в каждый интервал.
x_min, x_max	Минимальное и максимальное значения в списке.
delta	Длина каждого интервала.
x, i	Вспомогательные переменные для циклов.

Листинг 4 – Функция slicearray

def slicearray(array, intervals_cnt = 10): '''Функция для разбивки списка на интервалы и подсчета кол. попаданий''' interval=[] # Список интервалов entries = [] # Список кол-ва вхождений x_min, x_max = min(array), max(array) delta = (x_max - x_min) / intervals_cnt # Заполняем список интервалов for x in range (intervals_cnt+1): interval.append(x_min + delta * x) # Заполняем список кол-ва вхождений for i in range(intervals_cnt): entries.append(sum(True for x in array if interval[i] < x <= interval[i+1])) return interval, entries, x_min, x_max, delta

Описание функции slicearray:

1. Начало функции

2. Определение переменных interval и entries

3. Определение переменных x_min, x_max и delta

4. Заполнение списка interval

5. Заполнение списка entries с использованием условия interval[i] < x <= interval[i+1]

6. Возвращение interval, entries, x_min, x_max, delta

7. Конец функции

5. Функция ploting_lambda_nu(k, lmbda, lmbda_list, nu_list, N_array)

Функция строит графики зависимости оценок интенсивности и коэффициента вариации от объема выборки.

Список использованных переменных представлен в таблице 5. Программный код функции представлен в листинге 5.

Таблица 5 – Список используемых переменных функции ploting_lambda_nu

Название переменной	Описание
k	Порядок эрланговского потока
lamda	Параметр потока λ
lmbda_list, nu_list	Списки оценок интенсивности и коэффициента вариации.
N_array	Список значений объема выборки.
lambda_t, nu_t	Теоретические значения интенсивности и коэффициента вариации.
fig, axis	Объекты графиков.

Листинг 5 – Функция ploting_lambda_nu

def ploting_lambda_nu(k, lmbda, lmbda_list, nu_list, N_array): '''Ф-ция построения графиков зависимости оценок интенсивности и коэффициента вариации от объема выборки заданного потока''' # Расчет теоретических значений lambda_t = lmbda / k nu_t = 1 / np.sqrt(k) # Создаем объекты графиков fig, axis = plt.subplots(1, 2, figsize=(14, 7)) fig.suptitle('Статистика для Эрланговского распределения с k={} и lambda={}'.format(k, lmbda), fontsize=16) # Строим график зависимости оценок интенсивности от объема выборки axis[0].axhline(lambda_t, color='red', label='Теоретическое значение') axis[0].plot(N_array, lmbda_list, label='Рассчитанное значение') axis[0].set_title('График зависимости\nоценок интенсивности от объема выборки') axis[0].set_xlabel('Размер выборки') axis[0].set_ylabel('Оценка интенсивности') axis[0].legend() # Строим график зависимости оценок коэффициента вариации от объема выборки axis[1].axhline(nu_t, color='red', label='Теоретическое значение') axis[1].plot(N_array, nu_list, label='Рассчитанное значение') axis[1].set_title('График зависимости\nоценок коэффициента вариации от объема выборки') axis[1].set_xlabel('Размер выборки') axis[1].set_ylabel('Оценка коэффициента вариации') axis[1].legend() plt.show()

Описание функции ploting_lambda_nu:

1. Начало функции

2. Расчет теоретических значений lambda_t и nu_t

3. Создание объектов графиков

4. Построение графика зависимости оценок интенсивности от объема выборки

5. Построение графика зависимости оценок коэффициента вариации от объема выборки

6. Конец функции

6. Функция erlang_model(k, lmbda, N=10000)

Функция моделирует Эрланговское распределение и строит соответствующие графики.

Список использованных переменных представлен в таблице 6. Программный код функции представлен в листинге 6.

Таблица 6 – Список используемых переменных функции erlang_model

Название переменной	Описание
k	Порядок эрланговского потока
lamda	Параметр потока λ
N	Начальный объем выборки.
lmbda_old, nu_old	Старые оценки интенсивности и коэффициента вариации.
lmbda_list, nu_list	Списки для хранения оценок интенсивности и коэффициента вариации.
u_list	Список значений выборки Эрланговского распределения.
loop_cnt	Счетчик цикла.
N_array	Список значений объема выборки.
me, sigma	Оценки математического ожидания и дисперсии
lmbda_new, nu_new	Новые оценки интенсивности и коэффициента вариации.

Листинг 6 – Функция erlang_model

def erlang_model(k, lmbda, N=10000): '''Функция моделирования Эрланговского распределения''' # Текущая оценка интенсивности и коэффициента вариации потока lmbda_old, nu_old = 1, 1 # Списки оценок интенсивности и коэффициента вариации потока для разных N lmbda_list, nu_list = [], [] # Список значений выборки эрланговского распределения u_list = [] # Счетчик цикла loop_cnt = 0 # Список зничений объема выборки при которых производились # расчеты интенсивности и коэффициента вариации потока N_array = [] while True: # Добавляем N случайных значений эрланговского закона распределения u_list.extend(random_erlang_val(k, lmbda, N * 2**loop_cnt)) # Добавляем значение нового объема выборки N_array.append(len(u_list)) # Оценка Мат. ожидания и Дисперсии me = np.mean(u_list) sigma = np.std(u_list) # Оценка новых значений интенсивности и коэффициента вариации потока lmbda_new = 1/me nu_new = sigma/me # Добавление новых отценок в списки lmbda_list.append(lmbda_new) nu_list.append(nu_new) # Проверка достаточности выборки if abs((lmbda_new - lmbda_old) / lmbda_old) <= 0.01 and abs((nu_new - nu_old) / nu_old) <= 0.01: break # Перенос новых оценок на место старых lmbda_old = lmbda_new nu_old = nu_new loop_cnt += 1 if len(u_list) != N else 0 # Построение графика по сформированному распределению ploting_erlang_distribution(k, lmbda, data=u_list, add_hist=True) # Построение графика зависимости оценок интенсивности и коэффициента вариации потока ploting_lambda_nu(k, lmbda, lmbda_list, nu_list, N_array) return u_list, lmbda_list, nu_list

Описание функции erlang_model:

1. Начало функции

2. Определение начальных значений lmbda_old, nu_old, lmbda_list, nu_list, u_list, loop_cnt, N_array

3. Цикл, который продолжается до тех пор, пока разница между новыми и старыми оценками lmbda и nu не станет меньше или равной 0.01 (условие while abs((lmbda_new - lmbda_old) / lmbda_old) <= 0.01 and abs((nu_new - nu_old) / nu_old) <= 0.01)

   1. Добавление N случайных значений эрланговского закона распределения в u_list

   2. Добавление значения нового объема выборки в N_array

   3. Оценка математического ожидания и дисперсии

   4. Оценка новых значений lmbda_new и nu_new

   5. Добавление новых оценок в списки lmbda_list и nu_list

   6. Перенос новых оценок на место старых

4. Построение графика по сформированному распределению

5. Построение графика зависимости оценок интенсивности и коэффициента вариации потока

6. Возвращение u_list, lmbda_list, nu_list

7. Конец функции

3. Графики зависимости оценок интенсивности и коэффициента вариации от M. На графиках уровнем отметить теоретические значения эти величин;

График плотности вероятности, построенный по смоделированному Эрлановскому потоку представлен на рисунке 4.

Рисунок 4 – График плотности вероятности

Графики зависимости оценок интенсивности и коэффициента вариации от объема выборки представлены на рисунке 5. Уровнем отмечены теоретические значения эти величин.

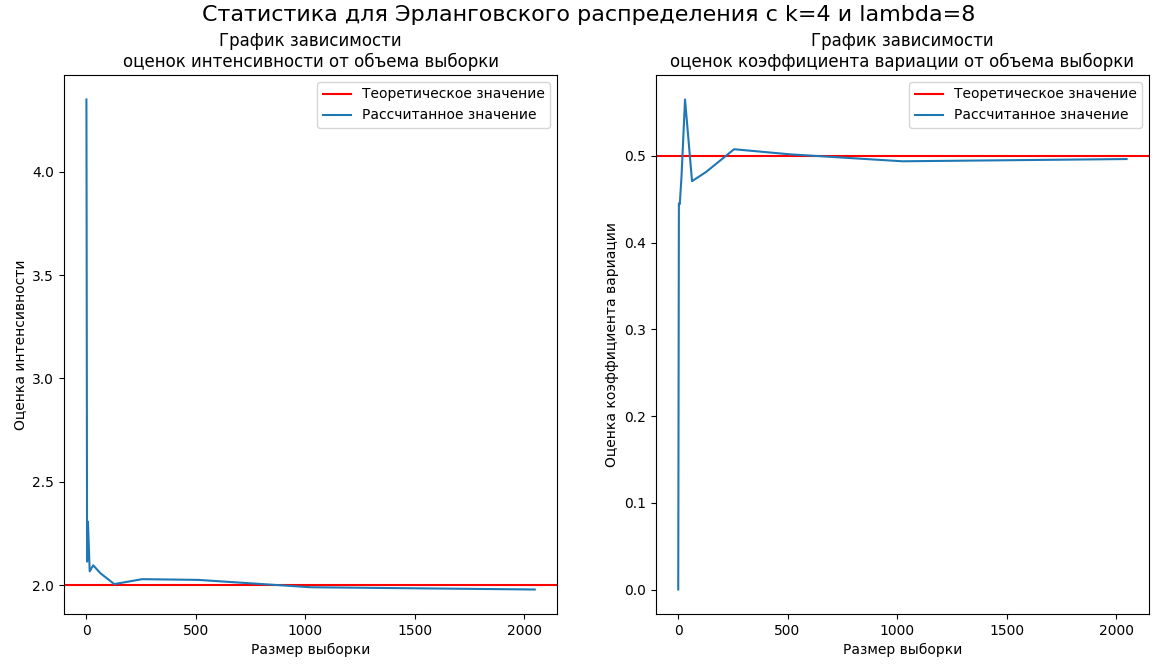Рисунок 5 – Графики зависимости оценок интенсивности и коэффициента вариации от N

ВЫВОД

В ходе выполнения лабораторной работы на тему “Моделирование входного потока запросов” были изучены основные характеристики входных потоков заявок и базовые принципы моделирования СМО по событиям.

В соответствии с вариантом был выбран закон распределения интервалов между двумя соседними заявками. Были рассчитаны теоретические значения интенсивности и вариации.

С помощью разработанной программы была реализована методика оценки интенсивности потока. Программа позволила произвести оценку интенсивности и коэффициента вариации заданного потока.

Был построен график зависимости оценок интенсивности и коэффициента вариации от величины выборки. Анализ графика показал, что с увеличением объема выборки оценочные значения постепенно приближаются к теоретическим, что подтверждает корректность выполнения работы и эффективность выбранного метода оценки.

Таким образом, лабораторная работа позволила глубже понять принципы моделирования входного потока запросов и применить теоретические знания на практике. Это будет полезно для дальнейшего изучения дисциплины и выполнения более сложных задач по моделированию систем массового обслуживания.

ПРИЛОЖЕНИЕ А. Код программы

from matplotlib import pyplot as plt

import numpy as np

def random_erlang_val(k, lmbda, N=10000):

'''Функция создающая случайное число распределенное по закону Эрланговского распределения'''

f = lambda : -1/lmbda * sum(np.log(np.random.uniform(0,1)) for i in range(k))

return [f() for n in range(N)]

def slicearray(array, intervals_cnt = 10):

'''Функция для разбивки списка на интервалы и подсчета кол. попаданий'''

interval=[] # Список интервалов

entries = [] # Список кол-ва вхождений

x_min, x_max = min(array), max(array)

delta = (x_max - x_min) / intervals_cnt

# Заполняем список интервалов

for x in range (intervals_cnt+1):

interval.append(x_min + delta * x)

# Заполняем список кол-ва вхождений

for i in range(intervals_cnt):

entries.append(sum(True for x in array if interval[i] < x <= interval[i+1]))

return interval, entries, x_min, x_max, delta

def ploting_erlang_distribution(k, lmbda, data = [], N=10000, iner_cnt = 50, add_hist=False):

'''Построение графика плотности Эрланговского распределения'''

plt.figure(figsize=(9,7))

# Проверка переданны ли дынные для построения гистограммы

if not data: data = random_erlang_val(k, lmbda, N)

else: N = len(data)

# Определение интервалов и их длительности, min/max значений для построения гистограммы

intervals, entries, x_min, x_max, delta = slicearray(data, iner_cnt)

# Проверка добавлять гистограмму или нет

if add_hist:

# Подсчет весов столбцов гистограммы

weights = [cnt / (N * delta) for cnt in entries]

plt.hist(intervals[:-1], intervals, weights = weights, label='Рассчитанное значение')

# Функция плотности вероятности эрланговского распределения для заданных k и lambda

f = lambda x : ((lmbda**k) * (x**(k-1)) * np.exp(-lmbda*x)) / np.math.factorial(k-1)

# Генерируем список значений x для построения графика

x = np.linspace(0 if x_min<=1 else x_min-1, x_max+1, 100)

plt.plot(x, f(x), label='График плотности вероятности\nЭрланговского распределения\nдля k={}, lambda={}'.format(k, lmbda), color='red')

plt.title("График плотности вероятности\nЭрланговского распределения", fontsize=16)

plt.xlabel("x")

plt.ylabel("y")

plt.legend()

plt.show()

def ploting_lambda_nu(k, lmbda, lmbda_list, nu_list, N_array):

'''Ф-ция построения графиков зависимости оценок интенсивности и коэффициента вариации от объема выборки заданного потока'''

# Расчет теоретических значений

lambda_t = lmbda / k

nu_t = 1 / np.sqrt(k)

# Создаем объекты графиков

fig, axis = plt.subplots(1, 2, figsize=(14, 7))

fig.suptitle('Статистика для Эрланговского распределения с k={} и lambda={}'.format(k, lmbda), fontsize=16)

# Строим график зависимости оценок интенсивности от объема выборки

axis[0].axhline(lambda_t, color='red', label='Теоретическое значение')

axis[0].plot(N_array, lmbda_list, label='Рассчитанное значение')

axis[0].set_title('График зависимости\nоценок интенсивности от объема выборки')

axis[0].set_xlabel('Размер выборки')

axis[0].set_ylabel('Оценка интенсивности')