Ответы к экзамену 4 семестр Мухачева Т. Л

То есть формула РэлеяДжинса является низкочастотным приближением к формуле Планка. Отсутствие в формуле РэлеяДжинса постоянной Планка является признаком того, что выражение может быть получено из классической физической теоремы.

С температурой излучения. Эта формула представляет собой закон смещения Вина.

Найдём выражение для объёмной плотности энергии равновесного электромагнитного излучения.

1)Излучение звёзд (излучение с поверхности звёзд с хорошей степенью точности характеризуется планковским спектром; Солнце даёт излучение с температурой 5770 K, что соответствует максимуму излучения в середине видимого диапазона частот (зелёному свету))

2)Реликтовое излучение – изотропное равновесное излучение, заполняющее всю Вселенную, температура которого уменьшается по мере расширения Вселенной (экспериментальное обнаружение этого излучения с температурой T ≈ 2,7K

7.Фотоны. Энергия и импульс фотона. Фотоэффект (виды, законы и их объяснение, уравнение Эйнштейна, красная граница, контактная разность потенциалов, задерживающая разность потенциалов).

Фотон – квант электромагнитного излучения. Они обладают дискретной энергией и импульсом. Фотоны движутся со скоростью света, имеют нулевую массу.

Энергия фотона (E) связана с его частотой (ʋ) через соотношение Планка: E = hʋ, где h - постоянная Планка. Чем выше частота света, тем больше энергия фотона.

Импульс фотона (p) связан с его длиной волны (λ) через соотношение де Бройля: p = h/λ. Чем короче длина волны света, тем больше импульс фотона.

Фотоэффект

Фотоэффект - явление, при котором свет падает на поверхность материала и вызывает выход электронов из этой поверхности. Фотоэффект был открыт Герцем.

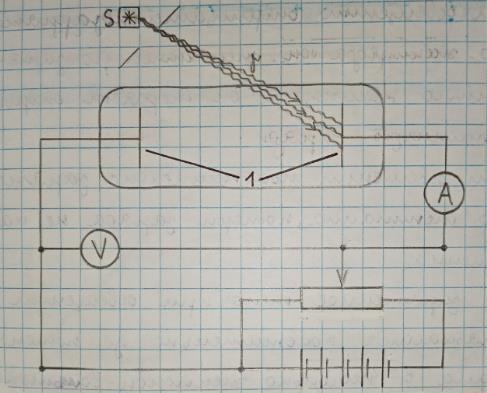
К металлическим электродам 1 может подаваться напряжение различной полярности. Они разделены вакуумным промежутком. Поверхность одного из электродов облучается излучением ультрафиолетовой части спектра. В результате из облучаемой поверхности вырываются электроны, которые дрейфуют на противоположный электрод и создают ток в цепи.

Виды фотоэффекта:

1.Внешний фотоэффект – явление вырывания электронов из вещества (металла, полупроводника, диэлектрика) под действием электромагнитного излучения ультрафиолетовой части спектра.

2.Внутренний фотоэффект – переходы электронов внутри полупроводника или диэлектрика из связанных состояний в свободные под действием ультрафиолетового излучения.

Законы фотоэффекта:

1)Первый закон – закон Столетова. При фиксированной частоте падающего света число фотоэлектронов, вызываемых из катода в единицу времени, пропорционально интенсивности падающего света (излучения)

2)Второй закон фотоэффекта. Максимальная начальная скорость фотоэффектов не зависит от интенсивности падающего света, а определяется только его частотой.

3)Третий закон. Для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота излучения, ниже которой фотоэффекта невозможен. Красная граница зависит от химической природы вещества и состояния его поверхности.

По Эйнштейну, фотоэффект – это рассеяние фотона на электроны.

Контактная разность потенциалов - разность потенциалов между поверхностью материала и внешней системой, в которую электроны влетают при фотоэффекте.

Задерживающая разность потенциалов - потенциал, применяемый к материалу для противодействия вылету электронов при фотоэффекте. Она равна контактной разности потенциалов минус работа выхода электрона.

8. Опыты Дэвидсона и Джермера Томсона и Тартаковского

Опыты Девиссона и Джермера, Томпсона и Тартаковского.

Пучок электронов рассеивается на кристалле никеля. Кристалл никеля служит естественной дифракционной решёткой. На экране, расположенном за кристаллом, наблюдалась система дифракционных колец, для которой дифракционные максимумы соответствовали формуле Вульфа-Брегга.

Томпсон и Тартаковский рассматривали быстрые электроны (≈50 кэВ), а Девиссон и Джермер – тепловые.

Опыт Тартаковского: Тартаковский рассматривал слабые электронные пучки. Промежуток времени между двумя соседними электронами в 104 раза больше, чем время, необходимое электрону для прохождения дифракционного прибора. Полученная при длительной экспозиции дифракционная картина не отличалась от дифракционных картин, полученных при которткой экспозиции для пучков с интенсивностью на порядок больше.

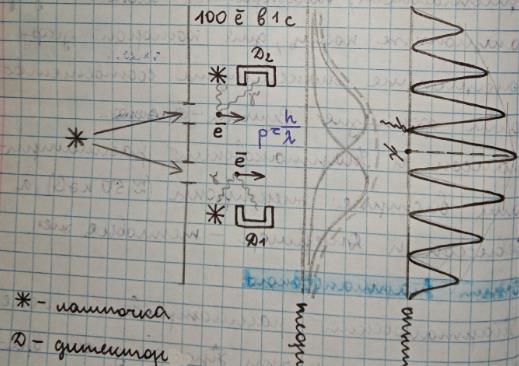
Во всех опытах электроны после прохождения кристалла попадают только в одну конкретную точку на фотопластинке, вызывая почернение только в ней и нигде больше.

В этом проявляются свойства электрона как частицы. Несмотря на одинаковые начальные условия электроны попадают в разные точки. О данном конкретном электроне заранее известно, в какую именно точку он попадёт. В этом проявляются волновые свойства электрона.

Дифракционная картина возникает, когда кристалл пройдёт достаточно больше количество электронов. Интенсивность почернения пластинки в данной точке пропорционально числу попавших в неё частиц, то есть вероятности попадания. Вероятность попадания определяется интенсивность волны, то есть квадратом модуля

волновых функций, то есть величина определяет вероятность обнаружить электрон в момент времени t в точке с радиус-вектором r, а волна де Бройля

– это волна вероятности.

9. Атом Резерфорда. Постулаты Бора. Спектры излучения атома водорода. (Вывод радиуса стационарной орбиты, полной энергии электрона в атоме водорода.) Достоинства и недостатки теории Бора.

Модель атома Резерфорда. Атом состоит из положительного заряженного ядра и окружающей его электронной оболочки.

Линейные размеры ядра 10-13≈10-12см

Линейные размеры самого атома в 105раз больше, при это 99,95% массы атома сосредоточено в ядре

У нейтрального атома число электронов в оболочке = заряду ядра, если за единицу принять элементарный заряд.

Если оболочка потеряет или приобретёт электрон, то атом станет заряженным полом.

Недостатки модели Резерфорда:

1)По законам классической электродинамики вращающийся вокруг ядра электрон должен непрерывно излучать электромагнитные волны, а значит, терять энергию, с потерей энергии приближаться к ядру и в конце упасть на него.

2)Модель Резерфорда не объясняет наблюдаемые на опыте спектры атомов. Из теории Резерфорда следует, что спектры непрерывны, а на опыте они состоят из узких спектральных линий.

Спектр атома водорода

Формула Бальмера:

–λ частота

-R – постоянная Ридберга

-m – квантовое число(определяет серию)

-n – определяет конкретную линию в данной серии = m+1

Спектральную линию с наибольшей длиной волны в данной серии называют главной линией серии. Линию, соответствующую числу m →∞, называют коротковолновой границей, к ней примыкает непрерывный спектр.

Модель Бора. Постулаты Бора:

1.В атоме существуют стационарные (неизменяющиеся во времени) состояния, находясь в которых атом не излучает энергию; эти состояния характеризуются дискретными значениями энергии и моментом импульса.

2.При переходе атома из одного состояния в другое излучается или поглощается фотон с энергией hʋ

Самый нижний по энергии уровень – это основной уровень, всё, что выше – это возбуждённые уровни.

Энергия ионизации – это энергия, необходимая для удаления электрона из атома, находящаяся в основном состоянии.

Энергия связи данного состояния – энергия, необходимая для удаления электрона из атома, находящаяся в данном возбуждённом состоянии.

Энергия возбуждения – энергия, которую необходимо сообщить атому, чтобы он перешёл из основного состояния в возбуждённое.

Энергия электрона в атоме может принимать только дискретные значения, то есть она квантуется.

10. Гипотеза де Бройля. Длина волны де Бройля для релятивистской и нерелятивистской частицы. Соотношения неопределенностей. Статистическая интерпретация волн де Бройля. Плоская волна де Бройля. Волновая функция. Статистическая интерпретация волновой функции. Условие нормировки вероятностей.

Гипотеза де Бройля. Корпускулярно-волновой дуализм имеет универсальный характер. Каждой массивной частице (обладающей массой_ можно поставить в соответствие длину волны де Бройля.

-E – полная энергия частицы

-p – импульс

Соотношения неопределённостей:

Гейзенберг выдвинул идею о принципиальной невозможности измерения определённых пар, связанных между собой характеристик так, чтобы они одновременно имели точное значение.

1. Соотношение для импульсов и координат

Невозможно одновременно точно измерить координату и соответствующую проекцию импульса.

2. Соотношение энергия-время

Из-за конечности времени жизни атомов в возбуждённом состоянии энергии не является точно определённым, поэтому частота излучённого фотона имеет неопределённость, а, следовательно, линии спектра размыты, что подтверждает опыт.

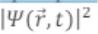- – вероятность обнаружить электрон в момент времени t в точке с радиус-

вектором . Значит волны де Бройля – волны вероятности

Статистическая интерпретация волн де Бройля:

Опыты показали, что частицы ведут себя как волны, а волны - как частицы. Но волну можно разделить на части, а частицы неделимы. В таком случае волновые свойства частиц можно трактовать только статистически. Частицы остаются частицами, но вероятность их появления в различных точках пространства подчиняется волновым законам.

Плоская волна де Бройля.

Статистическая интерпретация волновой функции: Вероятность нахождения частицы в момент времени t в единице объёма определяется квадратом модуля пси-функции