МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Факультет электроники Кафедра радиотехнической электроники

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к лабораторной работе №6.2 по дисциплине "Информационные технологии"

Доцент, к.т.н. И.А. Рябцев

Студент гр.0207 Б.И. Маликов<,,<

Санкт-Петербург 2021

Цель работы.

Изучение и программирование алгоритма построения выпуклой оболочки набора точек.

Задание.

Заданы множество S из n точек в двумерном пространстве; алгоритм вычисления полярного угла вектора 1-2; алгоритм построения выпуклой оболочки набора точек (Jarvis). Найти выпуклый многоугольник, содержащий все точки множества S:

1. Реализовать в Программе 1 в Matlab алгоритм вычисления полярного угла вектора 1-2 в виде функции.

2. Протестировать Программу 1 на наборе единичных векторов, начинающихся в начале координат po [0,0] и заканчивающихся в точках sx=[1, -1, -1, 1, 1]; sy=[1, 1, -1, -1, 1]. В полярной системе координат построить график polarplot для единичных векторов;

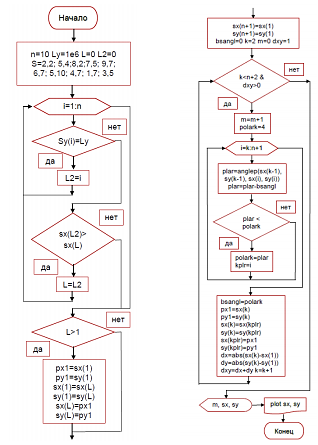
1. Реализовать в Программе 2 в Matlab алгоритм построения выпуклой оболочки набора точек (Jarvis) и вывода результатов (m – количество вершин многоугольника);

2. Оформить отчет, включив в него основную и модифицированную Программы 1 и 2; результаты тестирования Программы 1; исходные и конечные массивы sx, sy; копию построенного в Матлаб графика, подтверждающего полученную выпуклую оболочку.

Выполнение заданий.

1. Реализуем в Программе 1 в Matlab алгоритм вычисления полярного угла вектора 1-2 в виде функции. Протестируем Программу 1 на наборе единичных векторов, начинающихся в начале координат po [0,0] и заканчивающихся в точках sx=[1, -1, -1, 1, 1]; sy=[1, 1, -1, -1, 1]. В полярной системе координат построим график polarplot для единичных векторов:

function polar = anglePolar(x1, y1, x2, y2)

dx = x2-x1;

dy = y2-y1;

r = sqrt(dx.^2+dy.^2);

sns = dy/r;

ang = abs(asin(sns));

polar = ang;

if dy == 0 && dx < 0

polar = pi();

elseif dx == 0 && dy < 0

polar = 3/2*pi();

elseif dx < 0 && dy > 0

polar = pi() - ang;

elseif dx > 0 && dy < 0

polar = 2*pi() - ang;

elseif dx < 0 && dy < 0

polar = pi() + ang;

end

end

sx = [1, -1, -1, 1, 0, 1];

sy = [1, 1, -1, -1, 1, 0];

arr = zeros(1, 5);

for i = 1:5

arr(i) = anglepolar(0, 0, sx(i), sy(i));

end

polarplot(arr, ones(1, 5), "o", "MarkerFaceColor","k", "Color", "k");

Листинг результатов:

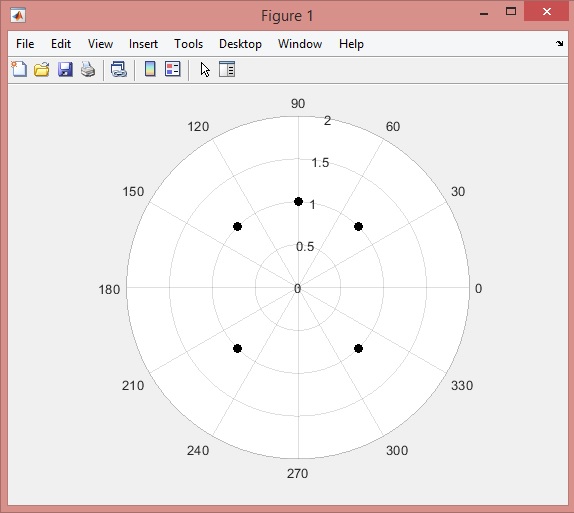
3. Реализуем в Программе 2 в Matlab алгоритм построения выпуклой оболочки набора точек (Jarvis) и вывода результатов (m – количество вершин многоугольника):

function polar = anglePolar(x1, y1, x2, y2)

dx = x2-x1;

dy = y2-y1;

r = sqrt(dx.^2+dy.^2);

sns = dy/r;

ang = abs(asin(sns));

polar = ang;

if dy == 0 && dx < 0

polar = pi();

elseif dx == 0 && dy < 0

polar = 3/2*pi();

elseif dx < 0 && dy > 0

polar = pi() - ang;

elseif dx > 0 && dy < 0

polar = 2*pi() - ang;

elseif dx < 0 && dy < 0

polar = pi() + ang;

end

end

n = 10;

l = 1;

l2 = 1;

s = [2, 2; 5, 4; 8, 2; 7, 5; 9, 7; 6, 7; 5, 10; 4, 7; 1, 7; 3, 5];

sx = [2 5 8 7 9 6 5 4 1 3 0];

sy = [2 4 2 5 7 7 10 7 7 5 0];

for i = 2:n

if sy(i) <= sy(l)

l2 = i;

end

if sx(l2) < sx(l)

l = l2;

end

end

if l > 1

px = sx(1);

py = sy(1);

sx(1) = sx(l);

sy(1) = sy(l);

sx(l) = px;

sx(l) = py;

end

sx(n+1) = sx(1);

sy(n+1) = sy(1);

bsangl = 0;

k = 2;

m = 0;

dxy = 1;

while (k < (n+2) && dxy > 0)

m = m+1;

polark = 100;

for i = k:(n+1)

polar = anglePolar(sx(k-1), sy(k-1), sx(i), sy(i));

if polar < polark && polar >= bsangl

polark = polar;

kplr = i;

end

end

bsangl = polark;

px = sx(k);

py = sy(k);

sx(k) = sx(kplr);

sy(k) = sy(kplr);

sx(kplr) = px;

sy(kplr) = py;

dx = abs(sx(k)-sx(1));

dy = abs(sy(k)-sy(1));

dxy = dx+dy;

k = k + 1;

end

plot(sx, sy, "o", "MarkerFaceColor","k", "Color", "k");

hold on;

plot(sx(1:m+1), sy(1:m+1), 'b-');

disp(m);

Листинг результатов:

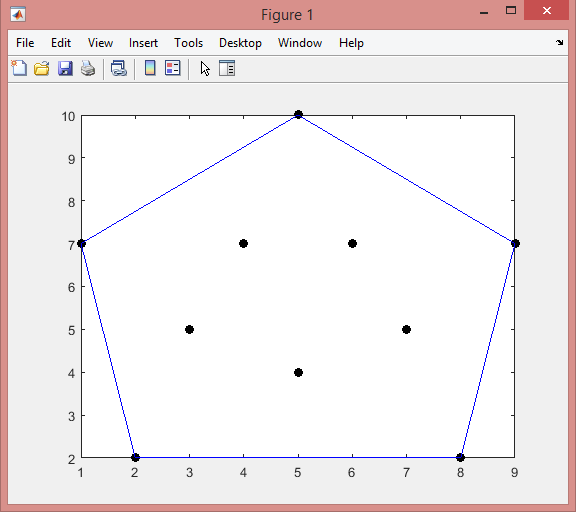
Вывод.

В ходе данной лабораторной работы были изучены: алгоритм вычисления полярного угла и алгоритм построения выпуклой оболочки набора точек (Jarvis). При этом, для каждой из задач были получены графики, опираясь на которые, можно сказать, что в данной лабораторной работе алгоритмы работают в полной форме.