МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Факультет электроники Кафедра радиотехнической электроники

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к лабораторной работе №5.2 по дисциплине "Информационные технологии"

Доцент, к.т.н. И.А. Рябцев

Студент гр.0207 Б.И. Маликов<,,<

Санкт-Петербург 2021

Цель работы.

Изучение и программирование стандартного алгоритма «бинарного поиска».

Задание.

Задан вектор исходных данных S(N) отсортированный по возрастанию значений его элементов, и алгоритм бинарного поиска индекса Nq, устанавливающего элемент массива S(Nq) = KEY.

1. Реализовать алгоритм бинарного поиска для вектора исходных данных S(10) в программе Matlab;

2. Вставить комментарии к операторам программы;

3. Вставить в программу стандартные функции tic, toc для оценки времени решения задачи;

4. Проверить программу Matlab на векторе исходных данных S(10);

5. Определить количество вызовов функции binary_search, используя глобальный счетчик (CM);

6. Получить листинг, включающий: вектор S(10), значение глобального счетчика CM и время решения задачи;

7. Модифицировать программу Matlab, задав исходный вектор S(100). Для этого установить размерность массива N=100;

8. Определить зависимость количество вызовов функции binary_search и время выполнения программы (наибольшее из 20 прогонов программы)для векторов S(10), S(100), S(1000), S(10⁴), S(10⁵), S(10⁶), S(10⁷);

9. Составить таблицу из семи строк (i=1-7), включив столбики с размерностью вектора, логарифмом размерности вектора, временем выполнения сортировки и количеством вызовов функции binary_search;

10. Рассчитать коэффициент пропорциональности А между логарифмом размерности вектора и количеством вызовов функции binary_search (CM=А lg N), используя инструмент тренда Excel или другим удобным способом;

11. Оформить отчет, включив в него тексты программ Matlab, листинг отсортированного вектора S(10), таблицу зависимости количества вызовов функции binary_search и времени решения задачи от размерности вектора. В выводы включить закономерность изменения количества вызовов функции binary_search от логарифма размерности вектора;

Выполнение заданий.

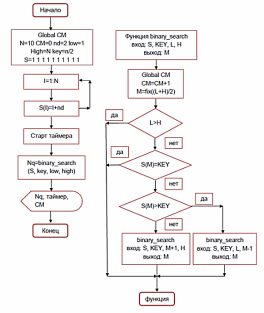
1. Реализуем алгоритм бинарного поиска для вектора исходных данных S(10) в программе Matlab:

Бинарный поиск:

function[M]=binary_search(S, key, low, high)

global CM

CM=CM+1; %вычисление вызова функции бинарного поиска

M=fix((low+high)/2);

if (low>high) %накладываем условие: если…, то повтор.

M=-1;

return;

end

if (S(M)==key) %накладываем условие: если…, то повтор.

return;

end

if (S(M)>key)

M=binary_search (S,key,low,M-1);

else

M=binary_search (S,key,M+1,high);

end

end

Выполнение алгоритма:

clear all

clc

global CM; %указываем исходные значения

CM=0;

N=10;

nd=2; %указываем значение шага

low=1;

high=N;

key=N;

S=ones(1,N);

for i=1:N

S(i)=i*nd-1;

end

tic; %начало отсчета времени

Nq=binary_search(S,key,low,high);

toc; %конец отсчета времени

disp (S); %вывод результатов

disp('Nq=');

disp(Nq);

disp('CM=');

disp(CM);

Листинг результатов:

Elapsed time is 0.010448 seconds.

Nq=

-1

CM=

4

2. Модифицируем программу:

clear all

clc

global CM

CM=0;

N=100;

nd=2;

low=1;

high=N;

key=N;

S=ones(1,N);

for i=1:N

S(i)=i*nd-1;

end

tic;

Nq=binary_search(S,key,low,high);

toc;

disp('Nq=');

disp(Nq);

disp('CM=');

disp(CM);

Листинг результатов:

Elapsed time is 0.014646 seconds.

Nq=

-1

CM=

7

1) N=10³

Листинг результатов:

Elapsed time is 0.020127 seconds.

Nq=

-1

CM=

10

2) N=10⁴

Листинг результатов:

Elapsed time is 0.036543 seconds.

Nq=

-1

CM=

14

3) N=10⁵

Листинг результатов:

Elapsed time is 0.040041 seconds.

Nq=

-1

CM=

17

4) N=10⁶

Листинг результатов:

Elapsed time is 0.063581 seconds.

Nq=

-1

CM=

20

5) N=10⁷

Листинг результатов:

Elapsed time is 0.083340 seconds.

Nq=

-1

CM=

24

3. Составим таблицу:

i	N	lg N	t*10^4, c	CM
1	10	1	104,5	4
2	100	2	146,5	7
3	1000	3	201,3	10
4	104	4	365,4	14
5	105	5	400,4	17
6	106	6	635,8	20
7	107	7	833,4	24

4. Построим график зависимости:

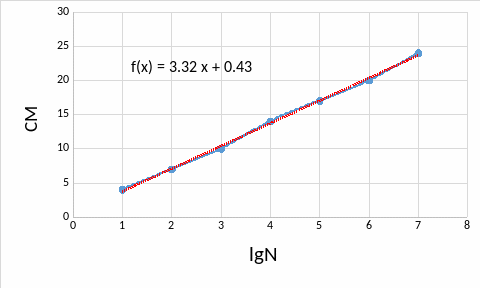
Таким образом, определили, что A = 3,32 (CM=3,32∙lgN)

Вывод.

В ходе данной лабораторной работы был изучен стандартного алгоритма «бинарного поиска». Также, анализируя закономерность изменения количества вызовов функции binary_search от логарифма размерности вектора, можно понять, что с увеличением количества вызовов функции логарифм размерности вектора также увеличивается, то есть линейная зависимость.