Лабы 2 Семестр / 0207 Маликов БИ Лабораторная работа №5.1

Министерство науки и высшего образования Российской Федерации

СПбГЭТУ «ЛЭТИ»

Кафедра высшей математики

Математический анализ

Типовой расчет по теме:

«Решение краевой задачи для обыкновенного дифференциального уравнения»

Вариант №25

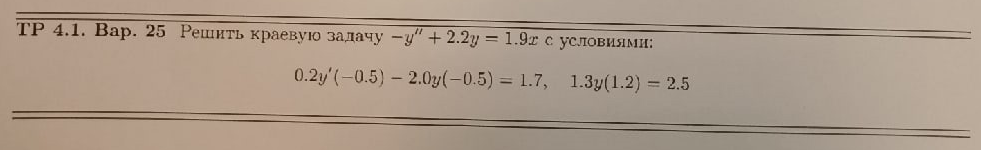
Выполнил: студент гр. №0207 Маликов Б. И.

Преподаватель: Трегуб В. Л.

Оценка: баллов

Санкт-Петербург

2022

I. Решение краевой задачи аналитическим методом.

1) Функцию y(x) найдем в виде:

y(x) = y₀(x) + (x)

1.1) Рассмотрим однородное дифференциальное уравнение:

- + 2,2y₀ = 0

Определим для него характеристическое уравнение, решим его и найдем корни:

- λ² + 2,2 = 0

λ² = 2,2

λ₁ = = 1,4832

λ₁ = - = - 1,4832

Соответственно, общее решение однородного уравнения:

y₀(x) = C₁e^1,4832x + C₂e^-1,4832x

1.2) Найдем частное решение неоднородного уравнения в виде: (x) = Ax+B, подставим (x) в неоднородное дифференциальное уравнение:

+ 2,2(Ax+B) = 1,9x

Тогда, получим:

=>

Следовательно:

(x) = 0,8636x

Общее решение неоднородного уравнения:

y(x) = C₁e^1,4832x + C₂e^-1,4832x + 0,8646x

2) Подставим y(x) в краевые условия. Найдем значения C₁ и C₂ методом Крамера:

(x) = 1,4832C₁e^1,4832x - 1,4832C₂e^-1,4832x + 0,8636

Используя метод Крамера:

△ = = - 2,2144e^-2,5214 + 2,9856e^2,5214

△₁ = = 0,8628e^-1,7798 + 2,6475e^0,7416

△₂ = = - 1,9637e^-0,7416 – 0,8628e^1,7798

Вычислим C₁ и С₂:

C₁ = = = 0,1542

C₂ = = = - 0,1636

Решение заданной краевой задачи:

y(x) = 0,1542e^1,4832x – 0,1636e^-1,4832x + 0,8636x

3) Разобьем промежуток [-0,5; 1,2] на пять равных частей и запишем значения y(x):

x_i = -0,5 + i = -0,5 + 0,34i

x	-0,5	-0,16	0,18	0,52	0,86	1,2
y(x)	-0,7018	-0,2240	0,2316	0,7069	1,2492	1,9230

II. Решение краевой задачи методом Фурье.

1) При помощи замены: y(x) = v(x) + αx + β, приведем краевые условия к однородным:

0,2 (-0,5) -2y(-0,5) = 0,2( (-0,5)+α) – 2(v(-0,5) – 0,5α + β) = 0,2 (-0,5) + 0,2α- - 2v(-0,5) + α – 2β = 0,2 (-0,5) – 2v(-0,5) + 1,2α - 2β = 1,7

1,3y(1,2) = 1,3(v(1,2) + 1,2α + β) = 2,5

Тогда:

=> =>

Таким образом: α = 1,5406; β = 0,0744. Получим:

y(x) = v(x) + 1,5406x + 0,0744

Подставив y(x) в уравнение, получим краевую задачу для функции v:



2) Рассмотрим оператор Штурма-Лиувилля: L(y) = + 2,2y. Найдем собственные числа и собственные функции этого оператора:

Запишем: - = (λ – 2,2)y. Обозначим: λ – 2,2 = μ² (μ 0).

Тогда, при μ² 0 общее решение уравнения + μ²y = 0:

y(x) = C₁cos(μ(1,2 – x)) +C₂sin(μ(1,2 – x))

Подставив в общее решение краевые условия, получим:

C₂ 0, если: 10sin(1,7μ) + μcos(1,7μ) = 0.

Тогда:

10sin(1,7μ) + μcos(1,7μ) = 0 | : cos(1,7μ)

10tg(1,7μ) + μ = 0

tg(1,7μ) =

График:

Найдем первые три корня уравнения:

₁ = 1,7463

₂ = 3,4980

₃ = 5,2592

Собственные числа оператора L(y) равны: λ_k = μ_k² + 2,2. Найдем первые три:

λ₁ = 5,2496

λ₂ = 14,4360

λ₃ = 29,8592

Тогда, собственные функции оператора L:

y_k(x) = sin(μ_k(1,2 – x))

Таким образом, для оператора L(y) получена система собственных чисел:

{λ_k = μ_k² + 2 и система собственных функций:{y_k = sin(μ_k(1,2 – x)) .

3) Найдем нормы функции y_k:

Разложим уравнение g(x) = -1,4893x – 0,1637 в ряд Фурье:

Коэффициенты Фурье g_k:

= ∙

Первые три коэффициента:

g₁ = - 0,78509 g₂ = - 0,84362 g₃ = - 0,27904

Решение для:

Будем искать в виде:

Учитывая, что:

Получим:

Тогда:

c_k =

Вычислим значения первых трех коэффициентов ряда:

c₁ = -0,149553 c₂ = -0,058439 c₃ = - 0,009345

Получим:

4) Решение исходной задачи примет вид:

5) В качестве приближенного решения задачи возьмем частичную сумму ряда Фурье:

В качестве примера, найдем значение y₃(x) в точке x₀ = -0,5. Значения y₃(x) в остальных точках приведем в таблице, при этом, составим таблицу с учетом значений y(x), полученных аналитическим методом:

x	-0,5	-0,16	0,18	0,52	0,86	1,2
y3(x)	-0,7067	-0,2246	0,2369	0,7003	1,2523	1,9231
y(x)	-0,7018	-0,2240	0,2316	0,7069	1,2492	1,9230