МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"
Факультет электроники Кафедра радиотехнической электроники
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА к лабораторной работе №4 по дисциплине "Информационные технологии"
Доцент, к.т.н. И.А. Рябцев
Студент гр.0207 Б.И. Маликов<,,<
Санкт-Петербург 2021
Цель работы.
Изучение и программирование стандартного алгоритма «быстрой сортировки».
Задание.
Задан алгоритм сортировки выбором и вектор исходных данных S(n):
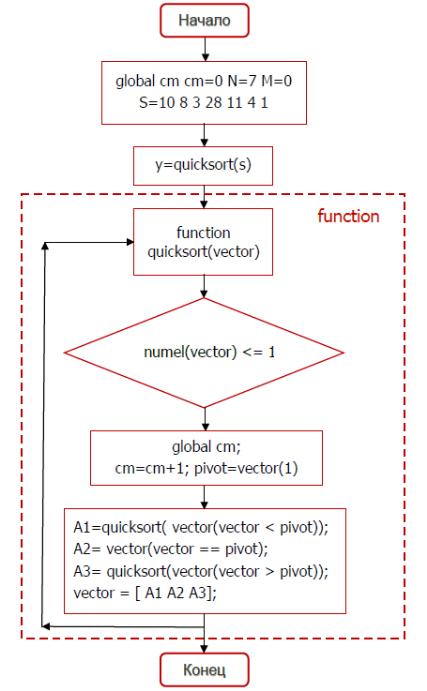
1. Реализовать алгоритм «быстрой» сортировки (по возрастанию) для вектора исходных данных S(7) в программе Matlab;
2. Вставить комментарии к операторам программы;
3. Вставить в программу стандартные функции tic, toc для оценки времени решения задачи;
4. Проверить программу Matlab на векторе исходных данных;
5. Определить количество вызовов функции quicksort, используя глобальный счетчик (сm);.
6. Получить листинг отсортированного вектора S(7);
7. Модифицировать программу Matlab, задав исходный вектор S(50). Для этого использовать функции rand и fix: s=fix(50*rand ([1 50])); выключить в отчет количество вызовов функции quicksort;
8. Определить зависимость количество вызовов функции quicksort для векторов S(80), S(100), S(150), S(200), S(250). Построить график зависимости;
9. Для векторов S(104), S(105), S(106), S(107) зафиксировать время выполнения программы (наибольшее из 20 прогонов программы) и соответствующее ему количество вызовов функции quicksort;
10. Составить в Excel таблицу из четырех строк (i=1, 2, 3, 4), включив столбики с размерностью вектора, временем выполнения сортировки и количеством вызовов функции quicksort.;
11. Рассчитать коэффициенты: KN=Nj/Ni, Kt=tj/ti для комбинаций i-i (1-2, 1-3, 1-4). Установить закономерность изменения времени сортировки от изменения размерности вектора (Kt ~ KN);
12. Оформить отчет, включив в него тексты программ Matlab, листинг отсортированного вектора S(7), таблицу времени выполнения от размерности вектора, таблицу с коэффициентами KN, Kt,;
13. В выводы включить закономерность изменения времени сортировки от изменения размерности вектора (Kt ~ KN) и закономерность изменения количества вызовов функции от размерности векторов;
Выполнение заданий.
1. Реализуем алгоритм «быстрой» сортировки (по возрастанию) для вектора исходных данных s(7) в программе Matlab;
Алгоритм быстрой сортировки:
function[vector]=quicksort(vector)
if ~isempty(vector)%накладываем условие
global cm;
cm=cm+1; %количество возовов команды
pivot=vector(1); %фиксированный опорный элемент
A1=quicksort(vector(vector<pivot)); %определяем границы
A2=vector(vector==pivot);
A3=quicksort(vector(vector>pivot));
vector=[A1 A2 A3]; %вывод
end
end
Реализация алгоритма:
clear all; %удалим все переменные из текущей рабочей области
clc;
global cm;%начальные условия
cm=0;
N=7; %значение количества элементов массива
s=[10 8 3 28 11 4 1]; %сам массив
tic; %начало отсчета времени
y=quicksort(s); %алгоритм быстрой сортировки
disp(s); %вывод исходного массива
disp(y); %вывод результата сортировки
disp (cm);
toc; %конец отсчета времени
Листинг результатов:
10 8 3 28 11 4 1
1 3 4 8 10 11 28
7
Elapsed time is 0.037977 seconds.
1.1 Модифицируем программу:
function[vector]=quicksort(vector)
if ~isempty(vector)
global cm;
cm=cm+1;
pivot=vector(1);
A1=quicksort(vector(vector<pivot));
A2=vector(vector==pivot);
A3=quicksort(vector(vector>pivot));
vector=[A1 A2 A3];
end
end
clear all;
clc;
global cm;
cm=0;
N=50;
M=0;
s=fix(50*rand ([1 50]));
tic;
y=quicksort(s);
disp(s);
disp(y);
disp (cm);
toc;
Листинг результатов:
Columns 1 through 20
21 45 9 13 7 6 43 28 27 7 42 31 17 25 20 3 11 6 9 11
Columns 21 through 40
20 2 45 47 24 24 16 45 18 5 39 19 12 20 4 6 47 47 28 2
Columns 41 through 50
11 17 41 0 2 8 32 36 32 22
Columns 1 through 20
0 2 2 2 3 4 5 6 6 6 7 7 8 9 9 11 11 11 12 13
Columns 21 through 40
16 17 17 18 19 20 20 20 21 22 24 24 25 27 28 28 31 32 32 36
Columns 41 through 50
39 41 42 43 45 45 45 47 47 47
32
Elapsed time is 0.078775 seconds.