Цель работы.

Изучение и программирование стандартного алгоритма «быстрой сортировки».

Задание.

Задан алгоритм сортировки выбором и вектор исходных данных S(n):

1.Реализовать алгоритм «быстрой» сортировки (по возрастанию) для вектора исходных данных S(7) в программе Matlab;

2.Вставить комментарии к операторам программы;

2

3.Вставить в программу стандартные функции tic, toc для оценки времени решения задачи;

4.Проверить программу Matlab на векторе исходных данных;

5.Определить количество вызовов функции quicksort, используя глобальный счетчик (сm);.

6.Получить листинг отсортированного вектора S(7);

7.Модифицировать программу Matlab, задав исходный вектор S(50). Для этого использовать функции rand и fix: s=fix(50*rand ([1 50])); выключить в отчет количество вызовов функции quicksort;

8.Определить зависимость количество вызовов функции quicksort для векторов S(80), S(100), S(150), S(200), S(250). Построить график зависимости;

9.Для векторов S(104), S(105), S(106), S(107) зафиксировать время выполнения программы (наибольшее из 20 прогонов программы) и соответствующее ему количество вызовов функции quicksort;

10.Составить в Excel таблицу из четырех строк (i=1, 2, 3, 4), включив столбики с размерностью вектора, временем выполнения сортировки и количеством вызовов функции quicksort.;

11.Рассчитать коэффициенты: KN=Nj/Ni, Kt=tj/ti для комбинаций i-i (1-2, 1- 3, 1-4). Установить закономерность изменения времени сортировки от изменения размерности вектора (Kt ~ KN);

12.Оформить отчет, включив в него тексты программ Matlab, листинг отсортированного вектора S(7), таблицу времени выполнения от размерности вектора, таблицу с коэффициентами KN, Kt,;

13.В выводы включить закономерность изменения времени сортировки от изменения размерности вектора (Kt ~ KN) и закономерность изменения количества вызовов функции от размерности векторов;

Выполнение заданий.

1. Реализуем алгоритм «быстрой» сортировки (по возрастанию) для вектора исходных данных S(7) в программе Matlab;

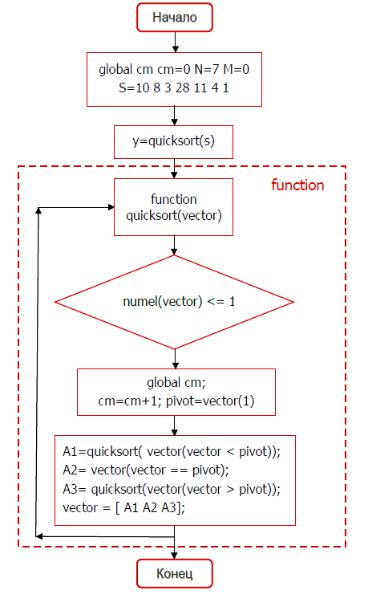
Алгоритм быстрой сортировки:

function[vector]=quicksort(vector)

if ~isempty(vector)%накладываем условие global cm;

3

cm=cm+1; %количество возовов команды pivot=vector(1); %фиксированный опорный элемент

A1=quicksort(vector(vector<pivot)); %определяем границы A2=vector(vector==pivot); A3=quicksort(vector(vector>pivot));

vector=[A1 A2 A3]; %вывод end

end

Реализация алгоритма:

clear all; %удалим все переменные из текущей рабочей области clc;

global cm;%начальные условия cm=0;

N=7; %значение количества элементов массива s=[10 8 3 28 11 4 1]; %сам массив tic; %начало отсчета времени

y=quicksort(s); %алгоритм быстрой сортировки disp(s); %вывод исходного массива

disp(y); %вывод результата сортировки disp (cm);

toc; %конец отсчета времени

Листинг результатов:

Elapsed time is 0.037977 seconds.

1.1 Модифицируем программу:

function[vector]=quicksort(vector) if ~isempty(vector)

global cm; cm=cm+1; pivot=vector(1);

A1=quicksort(vector(vector<pivot));

A2=vector(vector==pivot);

A3=quicksort(vector(vector>pivot)); vector=[A1 A2 A3];

end end

clear all; clc;

4

global cm; cm=0; N=50; M=0;

s=fix(50*rand ([1 50])); tic; y=quicksort(s); disp(s);

disp(y); disp (cm); toc;

Листинг результатов:

Elapsed time is 0.078775 seconds.

5

2. Определим зависимость количество вызовов функции quicksort для векторов S(80), S(100), S(150), S(200), S(250). Построим график зависимости:

1:

clear all; clc; global cm; cm=0; N=80; M=0;

s=fix(50*rand ([1 80])); tic; y=quicksort(s); disp(s);

disp(y); disp (cm); toc;

Листинг результатов:

Columns 1 through 20

Columns 61 through 80

38

Elapsed time is 0.048272 seconds.

В дальнейших вычислениях будем указывать только значение количества вызовов функции быстрой сортировки и значение занятого на это времени.

2:

clear all; clc; global cm; cm=0; N=100; M=0;

s=fix(50*rand ([1 100])); tic; y=quicksort(s); disp(s);

disp(y); disp (cm); toc;

Листинг результатов:

42

Elapsed time is 0.054458 seconds.

3:

clear all; clc; global cm; cm=0; N=150; M=0;

s=fix(50*rand ([1 150])); tic; y=quicksort(s); disp(s);

disp(y); disp (cm); toc;

Листинг результатов:

46

7

Elapsed time is 0.063415 seconds.

4:

clear all; clc; global cm; cm=0; N=200; M=0;

s=fix(50*rand ([1 200])); tic; y=quicksort(s); disp(s);

disp(y); disp (cm); toc;

Листинг результатов:

49

Elapsed time is 0.075983 seconds.

5:

clear all; clc; global cm; cm=0; N=250; M=0;

s=fix(50*rand ([1 250])); tic; y=quicksort(s); disp(s);

disp(y); disp (cm); toc;

Листинг результатов:

50

Elapsed time is 0.092237 seconds.

Построим график зависимости:

8

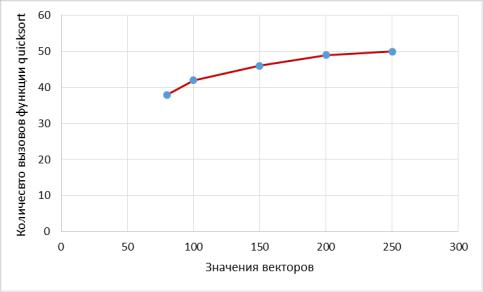
3. Для векторов S(104), S(105), S(106), S(107) зафиксируем время выполнения программы (наибольшее из 20 прогонов программы) и соответствующее ему количество вызовов функции quicksort:

1:

clear all; clc; global cm; cm=0; N=10^4; M=0;

s=fix(50*rand ([1 10^4])); tic; y=quicksort(s); disp(s);

disp(y); disp (cm); toc;

Листинг результатов:

50

Elapsed time is 0.243428 seconds.

2:

clear all; clc; global cm; cm=0; N=10^5; M=0;

s=fix(50*rand ([1 10^5])); tic; y=quicksort(s); disp(s);

9

disp(y); disp (cm); toc;

Листинг результатов:

50

Elapsed time is 1.161511 seconds.

3:

clear all; clc; global cm; cm=0; N=10^6; M=0;

s=fix(50*rand ([1 10^6])); tic; y=quicksort(s); disp(s);

disp(y); disp (cm); toc;

Листинг результатов:

50

Elapsed time is 14.273001 seconds.

4:

clear all; clc; global cm; cm=0; N=10^7; M=0;

s=fix(50*rand ([1 10^7])); tic; y=quicksort(s); disp(s);

disp(y); disp (cm); toc;

Листинг результатов:

50

Elapsed time is 139.744213 seconds.

10