
Лабы 1 Семестр / 0207 Маликов Отчет Лабораторная работа №10
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра физики
ОТЧЕТ
по лабораторной работе №10
ИССЛЕДОВАНИЕ ПРОЦЕССОВ ПЕРЕНОСА В ГАЗАХ
Выполнил: Маликов Б.И.
Группа № 0207
Преподаватель: Попов Ю.И.
Вопросы |
Задачи ИДЗ |
Даты коллоквиума |
Итог |
|||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
||||||||||
|
||||||||||
|
||||||||||
|
||||||||||
Санкт-Петербург
2020
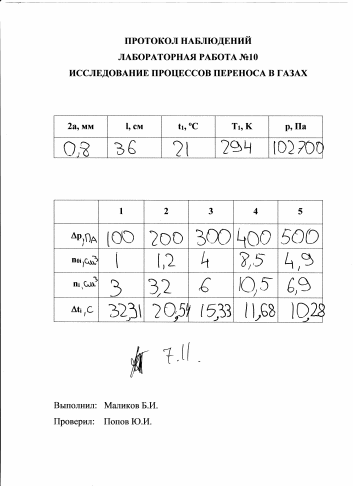
Цель работы.
Изучение явлений переноса в газе. Определение коэффициентов диффузии и вязкости воздуха, длины свободного пробега и эффективного диаметра его молекул.
Приборы и принадлежности.
Прибор для измерения объемной скорости истечения газа из трубки.
Прибор
для измерения объемной скорости течения
газа Q = V/t
(рис. 10.3) состоит из сосуда 1 с исследуемым
газом и сосуда 2, заполненного водой и
присоединенного к сосуду 1 гибкой
трубкой. Давление в сосуде 1 регулируется
перемещением по вертикали открытого
сосуда 2 и измеряется U-образным манометром
3 (1 мм вод. ст.
10 Па). Сосуд 1 сообщается с атмосферой
через кран 4 и узкую трубку 5. Положение
уровня жидкости и изменение объема газа
в сосуде 1 определяются по шкале 6. 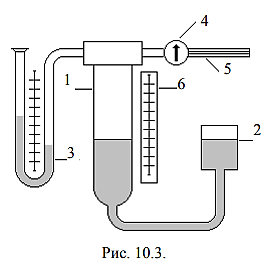
Исследуемые закономерности.
При нарушении равновесия в газе хаотическое движение молекул приводит к возникновению макроскопических потоков, стремящихся восстановить нарушенное равновесное состояние. Явления, возникающие при протекании этих процессов, называются явлениями переноса. К явлениям переноса относят диффузию, внутреннее трение (вязкость), теплопроводность. В данной работе исследуются первые два явления.
Внутреннее трение это явление, обусловленное переносом импульса молекул. Сила трения, возникающая между слоями газа, определяется как:
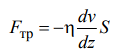
где коэффициент внутреннего трения (вязкости); v скорость отдельных слоев газа; dv/dz градиент скорости слоев газа в направлении, перпендикулярном к поверхности, разделяющей слои (в направлении оси z перпендикулярной скорости слоев v); S площадь соприкасающихся слоев.
Течение газа в узкой цилиндрической трубке. Пусть газ течет в трубке с радиусом a и длиной l (l >> a) под действием разности давлений p на концах трубки (рис. 10.2). В установившемся режиме (t > t3) изменение скорости течения газа по сечению трубки описывается параболической зависимостью:
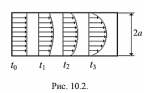
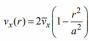
где
r
расстояние, отсчитываемое от оси трубки,
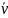 x
средняя по сечению скорость течения
газа.
x
средняя по сечению скорость течения
газа.
Расход газа связан со средней скоростью x соотношением Q=pa2 x , так что средняя скорость слоев газа по сечению трубки:

Приравнивая полученные выражения для x , получаем формулу для расчета коэффициента вязкости газа:
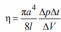
Диффузия это явление, обусловленное переносом массы молекул. Процесс диффузии описывается законом Фика:
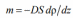
Кинетические
коэффициенты D и
зависят от средней скорости теплового
движения молекул u = (8RT/)1/2
и средней длины свободного пробега
( d2n)-1
молекул:
d2n)-1
молекул:
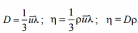
В формулах используются следующие обозначения: T температура газа; R = 8.31 Дж/(Кмоль) универсальная газовая постоянная; плотность газа; его молярная масса; d газокинетический или эффективный диаметр молекул; n – концентрация молекул газа.
Обработка результатов измерений.
Найдем вязкость воздуха η=
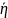
выборочным методом с Р = 95%:
выборочным методом с Р = 95%:
По
формуле: η=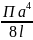 ∙
∙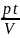
η1= ∙
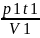 =
=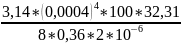 =45,09∙10-6
[Па∙с]
=45,09∙10-6
[Па∙с]η2= ∙
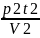 =
=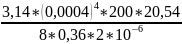 =57,32∙10-6
[Па∙с]
=57,32∙10-6
[Па∙с]η3= ∙
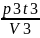 =
=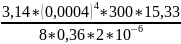 =64,18∙10-6
[Па∙с]
=64,18∙10-6
[Па∙с]η4= ∙
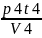 =
=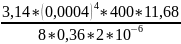 65,20∙10-6
[Па∙с]
65,20∙10-6
[Па∙с]η5= ∙
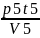 =
=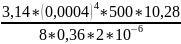 =71,73∙10-6
[Па∙с]
=71,73∙10-6
[Па∙с]
Упорядочим выборку в порядке возрастания:
η ={45,09∙10-6; 57,32∙10-6; 64,18∙10-6; 65,20∙10-6; 71,73∙10-6} [Па∙с]
1.2 Проверим выборку на наличие промахов.
Определим размах выборки: R=71,73∙10-6 - 45,09∙10-6 =26,64∙10-6 [Па∙с]
По таблице определим коэффициент Up,N при P=95% и N=5:
Up,N=0,64
Оценим на промахи каждую пару значений в выборке и сравним с Up,N:
η1=0,45<0,64 – не промах
η2=0,27<0,64 – не промах
η3=0,04<0,64 – не промах
η4=0,24<0,64 – не промах
Вывод: В данной выборке промахи отсутствуют.
1.3 Рассчитаем среднее выборочное значение:
=60,73∙10-6 [Па∙с]
1.4 Рассчитаем СКО среднего:
S =45,21∙10-7 [Па∙с]
Определим случайную погрешность по коэффициенту Стьюдента при N=5 и P=95%: tp,N=2,8 – по таблице;
η=126,62∙10-7 [Па∙с]
Рассчитаем полную погрешность результатов измерений:
=126,62∙10-7 [Па∙с]
Запишем результат измерений в округлённой форме:
η=(60,712,7) ∙10-6 [Па∙с]
Вычислим значение коэффициента диффузии воздуха D=
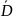
с Р = 95%:
с Р = 95%:
По
формуле: D= ,
где 𝝆=1,29
[кг/м3]
,
где 𝝆=1,29
[кг/м3]
=
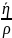 =
=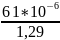 =47,28∙10-6
[м2/с]
=47,28∙10-6
[м2/с] =
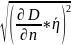 =10,07∙10-6
[м2/с]
=10,07∙10-6
[м2/с]Запишем результат измерений в округлённой форме:
D=(47,310,1) ∙10-6 [м2/с]
Оценим среднюю длину свободного пробега λ воздуха и газокинетический диаметр d его молекул:
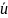 =
=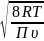 =
=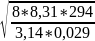 =463,29
[м/с]
=463,29
[м/с]
λ =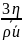 =3,05∙10-7
[м]
=3,05∙10-7
[м]
d=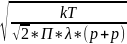 =1,71∙10-10
[м]
=1,71∙10-10
[м]
Рассчитаем теплопроводность воздуха cv, где cv iR/2 – его удельная теплоемкость (i=5) и сопоставим ее с табличным значением 24 мВт/(м К).
По формуле: cv iR/2=
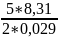 =716,37
[
=716,37
[ ]
]По формуле: cv=23 [
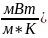
Сравним с табличным значением:
kт=24 [
k≈kт - значения приблизительно равны.
Рассчитаем Число Рейнольдса и стационарность течения газа в трубке:
По формуле: Re = 2a
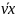 /D,
где
=
/D,
где
=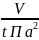 =0,22
[м/с]
=0,22
[м/с]
Re=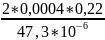 =3,8>2300
– турбулентность отсутствует, течение
ламинарное.
=3,8>2300
– турбулентность отсутствует, течение
ламинарное.
lст=0,1aRe=1,52∙10-4
Вывод.
В ходе данной лабораторной работы мы получили ряд данных, на основании которых смоги рассчитать значения для вязкости воздуха, коэффициента диффузии, теплопроводности и Числа Рейнольдса. Изучив полученные значения пришли к выводу, что течение газа ламинарное.
