Лабы 1 Семестр / 0207 Маликов Отчет Лабораторная работа №4

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра физики

ОТЧЕТ

по лабораторной работе №4

ПРОВЕРКА ТЕОРЕМЫ ГЮЙГЕНСА – ШТЕЙНЕРА МЕТОДОМ ВРАЩАТЕЛЬНЫХ КОЛЕБАНИЙ

Выполнил: Маликов Б.И.

Группа № 0207

Преподаватель: Попов Ю.И.

Вопросы		Задачи ИДЗ					Даты коллоквиума		Итог

Санкт-Петербург

2020

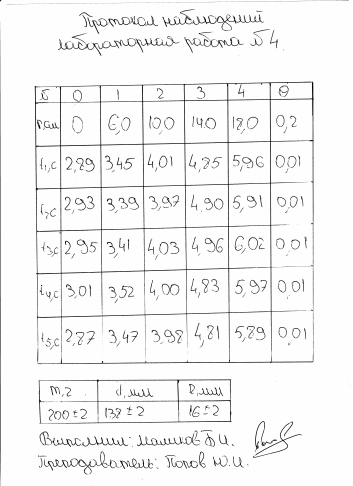
Цель работы.

Определение момента инерции эталонного диска методом вращательных колебаний и экспериментальная проверка теоремы Гюйгенса-Штейнера.

Приборы и принадлежности.

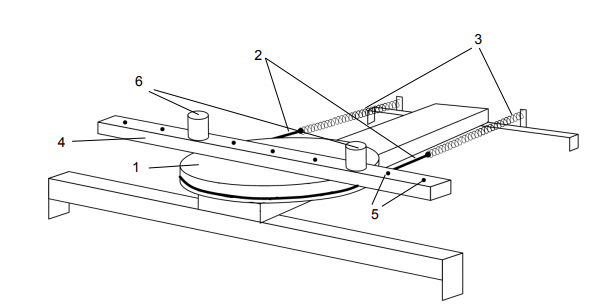
Лабораторная установка включает колебательную систему, вращающуюся в горизонтальной плоскости, которая состоит из закрепленного на вертикальной оси диска (шкива) 1, ремень 2 которого связан с упругими пружинами 3, зацепленными за штыри стойки. К шкиву жестко прикреплен металлический профиль 4 с рядом отверстий 5, в которых фиксируются грузы 6.

Основные теоретические положения.

В положении равновесия силы упругости пружин и силы натяжения нити с разных сторон диска (шкива) одинаковы. Обозначим эти силы F0. Для выведения шкива из положения равновесия повернем его на угол . По закону Гука силы упругости изменятся на kd/2, здесь k – коэффициент жесткости системы последовательно соединенных пружин, d – диаметр шкива. Тогда натяжение одной пружины увеличится, а другой уменьшится на kd/2, и на шкив будет действовать возвращающий момент сил:

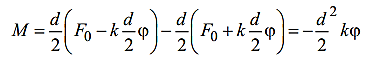
Подставляя в основное уравнение динамики вращательного движения:

и учитывая, что   , получаем дифференциальное уравнение для :

которое имеет вид дифференциального уравнения гармонического осциллятора. Из теории дифференциальных уравнений известно, что его решение имеет вид:

Здесь 0 и  – константы, определяемые начальными условиями, а - собственная частота колебаний маятника.

Если обозначить I₀, T₀, ₀ соответственно момент инерции, частоту и период системы, в которой грузы 6 помещены на металлическом профиле 4 в центр шкива 1, то согласно формуле :

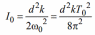
Если грузы переместить симметрично относительно оси вращения системы вдоль металлического профиля на шкиве в положения и т.д., то момент инерции I , частота  и период T колебательной системы изменятся, и ее момент инерции станет равным:

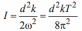
Отношение моментов инерции равно:

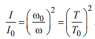
Если радиус цилиндров R , а их масса m, то при установке цилиндров на расстоянии r от оси вращения колебательной системы ее момент инерции равен:

Выражение для 0 I имеет вид:

Жесткость колебательной системы в данном эксперименте:

Обработка результатов измерений.

1. Рассчитаем параметры _I , T_i= _i/n , I_0i.

1.1

₀ = 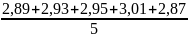=2,93 [c]

₁ = 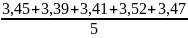=3,45 [c]

₂ = 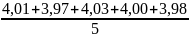=3,99 [c]

₃ = 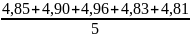=4,87 [c]

₄ = =5,95 [c]

1.2

T_i= _i/n

T_{0=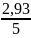 =0,59 [c]}

T_{1=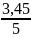 =0,69 [c]}

T_{2= =0,80 [c]}

T_{3=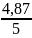 =0,97 [c]}

T_{4=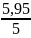 =1,19 [c]}

1.3

I₀=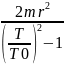

I₀₀=0

I₀₁=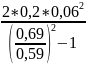 =0,0039 [кг∙м²]

I₀₂=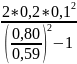 =0,0047 [кг∙м²]

I₀₃= =0,0046 [кг∙м²]

I₀₄=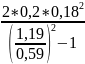 =0,0042 [кг∙м²]

Сопоставим значения моментов инерции колебательной системы:

I₀₁=0,0039 [кг∙м²]

I₀₂=0,0047 [кг∙м²]

I₀₃=0,0046 [кг∙м²]

I₀₄=0,0042 [кг∙м²]

I₀₁≈I₀₂≈I₀₃≈I₀₄

Вывод: значения моментов инерции колебательной системы приблизительно равны, что говорит о справедливости теоремы Гюйгенса-Штейнера.

2. Рассчитаем постоянную часть момента инерции колебательной системы I₀= 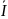_{0 0} c P=95%.

1. Упорядочим выборку в порядке возрастания:

I₀={0.0039; 0,0042; 0,0046; 0,0047} [кг∙м²]

2. Проверим выборку на наличие промахов.

Определим размах выборки: R=0,0047-0,0039=0,0008

По таблице определим коэффициент U_p,N при P=95% и N=4:

U_p,N=0,76

Оценим на промахи каждую пару значений в выборке и сравним с U_p,N:

I₁=0,38<0,76 – не промах

I₂=0,5<0,76 – не промах

I₃=0,13<0,76 – не промах

Вывод: В данной выборке промахов нет.

3. Рассчитаем среднее выборочное значение:

=0,0044[кг∙м²]

4. Рассчитаем СКО среднего:

S_I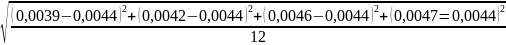^-= =0,0002

5. Определим случайную погрешность по коэффициенту Стьюдента при N=5 и P=95%: t_p,N=3,2 – по таблице;

=0,0006 [кг∙м²]

6. Рассчитаем полную погрешность результатов измерений:

=0,0006 [кг∙м²]

7. Запишем результат измерений в округлённой форме:

I₀=0,0044 0,0006 [кг∙м²]

3. Используя значения моментов инерции I₀ и двух цилиндров mR², рассчитаем момент инерции I_Д диска (шкива).

I₀=I_Д+mR²

I_Д=I₀-mR²

I_Д=0,0044-0,2∙0,016²=0,0043 [кг∙м²]

4. Рассчитаем жесткость колебательной системы k  с P=95%

k=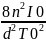

k=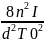 = =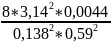52,4 [н/м]

k₁=46,4 [н/м]

k₂=55,9 [н/м]

k₃=54,7 [н/м]

k₄=50,0 [н/м]

4.1 Упорядочим выборку в порядке возрастания:

k={46,4; 50,0; 54,7; 55,9} [н/м]

4.2 Проверим выборку на наличие промахов.

Определим размах выборки: R=55,9-46,4=9,5

По таблице определим коэффициент U_p,N при P=95% и N=4:

U_p,N=0,76;

Оценим на промахи каждую пару значений в выборке и сравним с U_p,N:

I₁=0,38<0,76 – не промах

I₂=0,5<0,76 – не промах

I₃=0,13<0,76 – не промах

Вывод: В данной выборке промахов нет.

4.3 Рассчитаем среднее выборочное значение:

=52,4 [н/м]

4. Рассчитаем СКО среднего:

S_k^-=2,2

4. Определим случайную погрешность по коэффициенту Стьюдента при N=4 и P=95%: t_p,N=3,2 – по таблице;

k=7,1 [н/м]

4. Рассчитаем полную погрешность результатов измерений:

 =7,1 [н/м]

4. Запишем результат измерений в округлённой форме:

k=52,47,1 [н/м]

Вывод.

В ходе данной лабораторной мы получили данные, на основании которых смогли вычислить значения моментов инерции колебательной системы и определить, что эти значения приблизительно равны, доказав справедливость теоремы Гюйгенса-Штейнера. Также вычислили значение жёсткости колебательной системы.