Лабы 1 Семестр / 0207 Маликов Очет Лабораторная работа №2

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра физики

ОТЧЕТ

по лабораторной работе №2

ИССЛЕДОВАНИЕ ДИНАМИКИ СВОБОДНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ В ПОЛЕ СИЛЫ ТЯЖЕСТИ

Выполнил: Маликов Б.И.

Группа № 0207

Преподаватель: Попов Ю.И.

Вопросы		Задачи ИДЗ					Даты коллоквиума		Итог

Санкт-Петербург

2020

Цель работы.

Изучение закономерностей колебательного движения тела в однородном поле силы тяжести; исследование процессов превращения энергии в консервативных системах; определение момента инерции физического маятника.

Приборы и принадлежности.

Физический маятник; секундомер; масштабная линейка, чертежный треугольник.

На стержне 1 закреплены два диска – D1 и D2. Маятник может быть подвешен на кронштейне к легкой призме, трение в которой пренебрежимо мало.

Основные теоретические положения.

Физический маятник – это тело с распределенной массой или система тел, ось вращения которого расположена выше центра масс маятника. Относительно этой оси маятник колеблется с периодом:

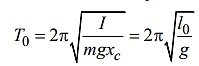
где для составного маятника m  m_i  масса маятника, x_c  m_ix_ci положение его центра масс относительно оси вращения, m_i и x_ci  масса i-го тела и положение его центра масс относительно оси вращения, I  I_i  полный момент инерции маятника, I_i=I_0i+m_ix²_ci – момент инерции i-го тела, рассчитанный относительно оси вращения по теореме Штейнера, I_0i  момент инерции этого тела относительно его центра масс.

Длина математического маятника, период которого совпадает с периодом колебаний данного физического маятника называется приведенной длиной физического маятника. Ее можно найти l₀=I/mx_c=gT₀²/4 ².

Полный момент инерции маятника может быть представлен в виде:

где - средний квадрат положений центров масс системы тел, составляющих маятник.

Если период колебаний маятника определен экспериментально, то из можно найти момент инерции маятника:

Сохранение энергии гармонических колебаний.

Потенциальная энергия при достижении амплитудного значения угла отклонения маятника равна:

где h_с  высота поднятия центра масс маятника при его максимальном отклонении от положения равновесия, x_с – положение центра масс маятника относительно его точки подвеса, _m - максимальный угол отклонения маятника от положения равновесия.

При малых углах отклонения маятника (до 20°) максимальная потенциальная энергия равна:

Максимальная кинетическая энергия физического маятника:

где момент инерции маятника выражен по формуле через период его колебаний. Из закона сохранения полной механической энергии:

можно найти максимальную угловую скорость маятника при прохождении им положения равновесия:

Обработка результатов измерений.

1. Рассчитаем время n 10 колебаний маятника t= c P=95%:

	1	2	3	4	5
t,c	12,00	11,54	11,80	11,62	11,37

1. Упорядочим выборку в порядке возрастания:

t={11,37; 11,54; 11,62; 11,80; 12,00} [c]

2. Проверим выборку на наличие промахов.

Определим размах выборки: R=12,00-11,37=0,63

По таблице определим коэффициент U_p,N при P=95% и N=5:

U_p,N=0,64

Оценим на промахи каждую пару значений в выборке и сравним с U_p,N:

t₁= =0,27<0,64 – не промах

t₂= =0,13<0,64 – не промах

t₃= =0,29<0,64 – не промах

t₄= =0,32<0,64 – не промах

Вывод: В данной выборке промахов нет.

3. Рассчитаем среднее выборочное значение:

= =11,67 [c]

4. Рассчитаем СКО среднего:

S_t^-= =

=0,11

5. Определим случайную погрешность по коэффициенту Стьюдента при N=5 и P=95%: t_p,N=2,8 – по таблице;

=t_p,N∙ S_t^-=2,8·0,11=0,31 [c]

6. Определим приборную погрешность Ɵ:

В данном случае Ɵ=0,01 [c];

7. Рассчитаем полную погрешность результатов измерений:

= =0,31 [c]

8. Запишем результат измерений в округлённой форме:

t=11,67 0,31 [c]

2 Рассчитаем период T=t/n колебаний маятника T₀=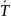 с P=95%

	1	2	3	4	5
T, с	1,200	1,154	1,180	1,162	1,137

1. Упорядочим выборку в порядке возрастания:

T={1,137; 1,154; 1,162; 1,180; 1,200} [c]

2. Проверим выборку на наличие промахов.

Определим размах выборки: R=1,200-1,137=0,063

По таблице определим коэффициент U_p,N при P=95% и N=5:

U_p,N=0,64

Оценим на промахи каждую пару значений в выборке и сравним с U_p,N:

T₁=0,27<0,64 – не промах

T₂=0,13<0,64 – не промах

T₃=0,29<0,64 – не промах

T₄=0,32<0,64 – не промах

Вывод: В данной выборке промахов нет.

3. Рассчитаем среднее выборочное значение:

=1,167 [c]

4. Рассчитаем СКО среднего:

S_T^-=0,01

5. Определим случайную погрешность по коэффициенту Стьюдента при N=5 и P=95%: t_p,N=2,8 – по таблице;

=0,030 [c]

6. Определим приборную погрешность Ɵ:

В данном случае Ɵ=0,01 [c];

7. Рассчитаем полную погрешность результатов измерений:

=0,030 [c]

8. Запишем результат измерений в округлённой форме:

T₀=1,167 0,030 [c]

2. Рассчитайте по формуле момент инерции маятника I= c P=95% относительно оси подвеса:

По формуле I=mgx_cT₀²/4п² рассчитаем значение момента инерции маятника и занесем в таблицу:

	1	2	3	4	5
I, кг∙м2	0,184	0,170	0,178	0,172	0,165

1. Упорядочим выборку в порядке возрастания:

I={0,165;0,170;0,172;0,178;0,184} [кг∙м²]

2. Проверим выборку на наличие промахов.

Определим размах выборки: R=0,184-0,165=0,019;

По таблице определим коэффициент U_p,N при P=95% и N=5:

U_p,N=0,64;

Оценим на промахи каждую пару значений в выборке и сравним с U_p,N:

I₁=0,26<0,64 – не промах

I₂=0,11<0,64 – не промах

I₃=0,32<0,64 – не промах

I₄=0,32<0,64 – не промах

Вывод: В данной выборке промахов нет.

3. Рассчитаем среднее выборочное значение:

=0,174 [кг∙м²]

4. Рассчитаем СКО среднего:

S_I^-=0,003

5. Определим случайную погрешность по коэффициенту Стьюдента при N=5 и P=95%: t_p,N=2,8 – по таблице;

=0,008 [кг∙м²]

6. Рассчитаем полную погрешность результатов измерений:

=0,008 [кг∙м²]

7. Запишем результат измерений в округлённой форме:

I=0,174 0,008 [кг∙м²]

2. По формуле W_pm= mgx_cф_m², где x_c и ф_m – измеренные значения параметров, рассчитаем полную механическую энергию маятника pm W=W_pm:

W_pm= ∙1,8∙10∙0,28∙(0,087)²=0,02 [Дж]

2. Рассчитаем приведенную длину маятника l₀=I/mx_c=gT₀²/4п²:

l₀=10∙(1,167)²/4∙(3,14)²=0,35 [м]

2. Рассчитаем массы m₁, m₂ дисков маятника и его стержня m₃. Для проверки правильности расчетов сопоставим сумму этих масс с полной массой маятника m:

m₁=ρ∙V= ρ∙S∙h= ρ∙ ∙h=8,7∙10³∙ ∙0,0257=0,75 [кг]

m₁=m₂=0,75 [кг]

m₃= ρ∙V= ρ∙S∙l= ρ∙ ∙l=8,7∙10³∙ ∙0,61=0,42 [кг]

m_общ= _i=0,75+0,75+0,42=1,92 [кг]

m_{общ.табл}=1,8 [кг]

m_общ≈m_{обш.табл}

2. Рассчитаем положение центра масс маятника c x и сопоставим его со значением, определенным экспериментально:

X_c= ∙ _ix_i= =0,3 [м]

X_сэксп = 0,28 [м]

X_c≈X_cэксп

Значения приблизительно равны.

2. Рассчитаем по теореме Штейнера моменты инерции каждого из тел составного маятника и его полный момент инерции I= _i.

I₀₁= = =4∙10^-4 [кг∙м²]

I₁=4∙10^-4+0,75∙0,265²=0,05 [кг∙м²]

I₀₂= = =4∙10^-4 [кг∙м²]

I₂=4∙10^-4+0,75∙0,373²=0,1 [кг∙м²]

I₀₃= =0,01 [кг∙м²]

I₃=0,01+0,42∙0,24²=0,03 [кг∙м²]

I=I₁+I₂+I₃=0,05+0,1+0,03=0,18 [кг∙м²]

Сопоставим его значение с определенным экспериментально в пункте 3:

I_р⁼0,18 [кг∙м²] I=0,174 [кг∙м²]

I_р≈I

Значения приблизительно равны.

Вывод.

В ходе данной лабораторной работы мы получили ряд данных, на основании которых в дальнейшем определили момент инерции для трех тел. Также, на основании этих данных мы рассчитали полную механическую энергию маятника. Сравнили значения положения центра масс и момента инерции, полученных экспериментально и вычисленных в результате обработки данных, и доказали, что значения приблизительно равны.