Лабы 1 Семестр / 0207 Маликов Отчет Лабораторная работа №9

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра физики

ОТЧЕТ

по лабораторной работе №9

ИССЛЕДОВАНИЕ ТЕРМОДИНАМИЧЕСКИХ ЦИКЛОВ

Выполнил: Маликов Б.И.

Группа № 0207

Преподаватель: Попов Ю.И.

Вопросы		Задачи ИДЗ					Даты коллоквиума		Итог

Санкт-Петербург

2020

Цель работы.

Исследование политропно-изохорно-изотермического (nVT) и адиабатно-изохорно-изотермического (SVT) циклов.

Приборы и принадлежности.

Баллон с воздухом, манометр, микрокомпрессор, лабораторные термометр и барометр.

Используемая в работе установка изображена на рис. 9.1. Баллон А объёмом V1 может сообщаться либо с насосом H, либо с атмосферой. Внутрь баллона помещён манометр М, измеряющий избыточное давление. Одно деление шкалы равно 4 мм вод. ст., что составляет 40 Па. Рабочим газом является воздух. В исходном состоянии параметры состояния воздуха следующие: внешнее давление p2 и комнатная температура T1. Диаграмма исследуемого цикла в координатах (p,V) показана на рис. 9.2.

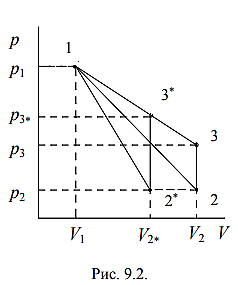
Исследуемые закономерности.

В работе изучается политропно-изохорно-изотермический (nVT) цикл. Для сравнения с nVT циклом используется адиабатно-изохорноизотермический (SVT) цикл, отличающийся тем, что процесс расширения газа на участке 12* рассматривается как адиабатический.

Первое начало термодинамики для политропного процесса имеет вид:

где C – теплоемкость воздуха в политропном процессе, C_V = C_v  C.

Уравнение Пуассона для политропного процесса TV^n1 = const или рVⁿ = const, где n – показатель политропы:

где С_p и C_v  теплоемкости газа в изобарном и изохорном процессах.

При относительно малых изменениях p и V угловые коэффициенты политропы 12 и изотермы 13 (см. рис. 9.2) рассчитывается по формулам:

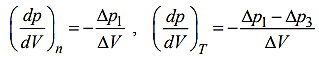
где V = V₂  V₁. Из этих и приведенных выше соотношений получаем формулу:

Зная n, можно определить мольную теплоемкость газа в политропном процессе:

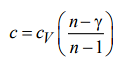
Работа расширения (сжатия) газа в политропическом A12 и изотермическом A13 процессах может быть рассчитана по формулам:

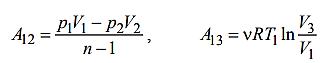
Для SVT-цикла холодильный коэффициент  равен:

А для nVT –цикла:

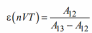
Получим:

Функция состояния, дифференциалом которой является отношение Q / T, называется энтропией:

В политропном процессе (на участке 1-2) изменение энтропии S равно:

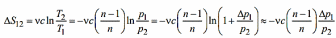
В изохорном процессе (на участке 23) изменение энтропии равно:

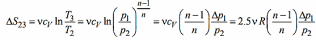
В изотермическом процессе (на участке 31):

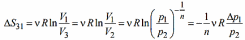
Для SVT-цикла изменение энтропии в адиабатном процессе (на участке 12 * ) равно нулю. С учетом, что изменение энтропии в цикле также рано нулю, заключаем, что изменения энтропии в изохорном и изотермическом процессах равны по величине, но различаются знаком:

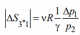
Обработка результатов измерений.

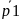
1. Рассчитаем в делениях шкалы манометра избыточные давления p₁    ( с P=95%.

1. Упорядочим выборку в порядке возрастания:

p₁ ={650; 700; 710; 720; 720; 720; 730; 730; 740; 750} [Па]

1.2 Проверим выборку на наличие промахов.

Определим размах выборки: R=750-650=100

По таблице определим коэффициент U_p,N при P=95% и N=10:

U_p,N=0,41

Оценим на промахи каждую пару значений в выборке и сравним с U_p,N:

p₁₁=0,5>0,41 – промах

p₁₂=0,1<0,41 – не промах

p₁₃=0,1<0,41 – не промах

p₁₄=0<0,41 – не промах

p₁₅=0<0,41 – не промах

p₁₆=0,1<0,41 – не промах

p₁₇=0<0,41 – не промах

p₁₈=0,1<0,41 – не промах

p₁₉=0,1<0,41 – не промах

Вывод: в данной выборке присутствует один промах.

1.3 Рассчитаем среднее выборочное значение:

 =724,4 [Па]

1.4 Рассчитаем СКО среднего:

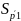=5,03

1.5 Определим случайную погрешность по коэффициенту Стьюдента при N=9 и P=95%: t_p,N=2,3 – по таблице;

(p₁)=11,6 [Па]

1.6 Рассчитаем полную погрешность результатов измерений:

( =11,6 [Па]

1.7 Запишем результат измерений в округлённой форме:

p₁=72412 [Па]

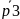
1. Рассчитаем в делениях шкалы манометра избыточные давления p₃    ( ) c P=95%

1.1.1 Упорядочим выборку в порядке возрастания:

p₃ ={110; 110; 120; 120; 120; 130; 130; 130; 140; 160} [Па]

1.1.2 Проверим выборку на наличие промахов.

Определим размах выборки: R=160-110=50

По таблице определим коэффициент U_p,N при P=95% и N=10:

U_p,N=0,41

Оценим на промахи каждую пару значений в выборке и сравним с U_p,N:

p₃₁=0<0,41 – не промах

p₃₂=0,2<0,41 – не промах

p₃₃=0<0,41 – не промах

p₃₄=0<0,41 – не промах

p₃₅=0,2<0,41 – не промах

p₃₆=0<0,41 – не промах

p₃₇=0<0,41 – не промах

p₃₈=0,2<0,41 – не промах

p₃₉=0,4<0,41 – не промах

Вывод: в данной выборке промахи отсутствуют.

1.1.3 Рассчитаем среднее выборочное значение:

 =127 [Па]

1.1.4 Рассчитаем СКО среднего:

=4,7

1.1.5 Определим случайную погрешность по коэффициенту Стьюдента при N=10 и P=95%: t_p,N=2,3 – по таблице;

(p₃)=10,8 [Па]

1.1.6 Рассчитаем полную погрешность результатов измерений:

( =10,8 [Па]

1.1.7 Запишем результат измерений в округлённой форме:

p₃=12711 [Па]

2. Рассчитаем показатель политропы n  с Р = 95% на участке 1–2 nVT цикла.

2.1 По формуле: n=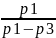

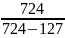= = =1,21

2.2

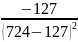= = =-0,0003

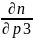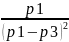= =0,002

2.3

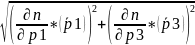 = =0,02

2.4

Запишем результат измерений в округленной форме:

n=1,210,02

3. Рассчитаем давления p1 и p3 , выразив их в Па.

p₁=p₂+p₁=101900+724=102624 [Па]

p₃=p₂+p₃=101900+127=102027 [Па]

4. Рассчитаем параметры состояния (p,V,T) в точках 1, 2 и 3 nVT-цикла, а также в точках 1^* , 2^* и 3^* SVT-цикла, используя уравнения политропического и адиабатического процессов.

1. Состояние 1:

p₁=102624 [Па]

V₁=22,4 [л]=22,4∙10^-3 [м³]

T₁=297 [К]

Состояние 1^*:

p₁^*=p1=102624 [Па]

V₁^*=V₁ =22,4 [л]=22,4∙10^-3 [м³]

T₁^*=T₁ =297 [К]

2. Состояние 2:

p₂=101900 [Па]

Уравнение политропы:

p₁V₁ⁿ=p₂V₂ⁿ

n=1,2

V₂=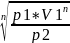 = =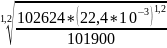0,02252 [м³]

=

T₂=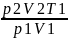 =296,6 [К]

Состояние 2^*:

p₂^*=p₂=101900 [Па]

ɣ= =1,4, при i=5

p₁V₁^*=p₂^*V₂^*

V₂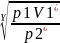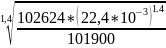^*= = =0,02251 [м³]

T₂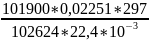^*= = =296,4 [К]

3. Состояние 3:

p₃=102027 [Па]

T₃=297 [К]

V₃= = =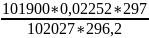0,02252 [м³]

Состояние 3^*:

T₃^*=297 [К]

p₃^*V₃^*=p₁V₁

V₃^*=V₂^*

p₃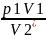^*= =102123 [Па]

=

V₃^*= = =0,02251 [м³]

	1	1*	2	2*	3	3*
p, Па	102624	102624	101900	101900	102027	102123
V, м3	0,0224	0,0224	0,02252	0,02251	0,02252	0,02251
T, К	297	297	296,6	296,4	297	297

5. Построим nVT- и SVT-циклы в координатах (р, V):

6. Рассчитаем изменения внутренней энергии, величину работы газа и поглощаемое (отдаваемое) им количество теплоты для всех процессов nVT цикла.

Изменение внутренней энергии:

1-2: U₁₂=υC_υ(T₂-T₁)

υ=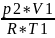 =0,925 [моль]

C_υ= =20,78 [ ]

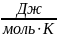U₁₂=-15,38 [Дж]

2-3: U₂₃=-U₁₂=15,38 [Дж]

3-1: U₃₁=0

Работа газа:

1-2: A₁₂= =19,8 [Дж]

2-3: A₂₃=0

1-3: A₃₁=υRT­₁ln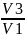 =12,2 [Дж]

Количество теплоты:

1-2: Q₁₂=4,42 [Дж]

2-3: Q₂₃=15,38 [Дж]

3-1: Q₃₁=12,2 [Дж]

7. Рассчитаем холодильные коэффициенты для nVT- и SVT-циклов;

ε(nVT)=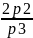 =1604

ε(SVT)= = =914

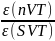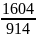= =1,8>1

Обратимый цикл Карно:

1. T₁,T₂:

ε_к=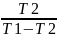 =742

T₁,T₂^*:

ε _k*= =494

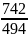= =1,5>1

Холодильные коэффициенты для nVT- и SVT-циклов больше холодильных коэффициентов цикла Карно.

8. Используя уравнения состояния идеального газа, найдем число молей воздуха в сосуде  по известным значениям p2, V1, T1:

υ= =0,925 [моль]

9. Рассчитаем мольную теплоемкость c_V воздуха при постоянном объеме и его мольную теплоёмкость c в политропном процессе:

C_υ= =20,78 [

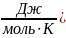
C= C_υ( )

ɣ= =1,4

C=-20,78 [

10. Рассчитаем изменение энтропии всех процессов в nVT- и SVT- циклах:

nVT:

Политропа 1-2: S₁₂= υ∙C∙(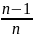 )∙ln =22,7∙10^-3 [

Изохора 2-3: S₂₃= 2,5υ∙R∙( )∙ =22,8∙10^-3 [

Изотерма 3-1: S₃₁=-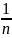 υ∙R∙ =-45,5∙10^-3 [

SVT:

Aдиабата 1^*-2^*: S₁₂=0

Изохора 2^*-3^*: S₂₃= υ∙R∙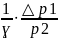 =40,1∙10^-3 [

Изотерма 3^*-1^*: S₃₁= -υ∙R∙ =-40,1∙10^-3 [

Вывод.

В ходе данной лабораторной работы мы получили ряд данных, на основании которых смогли определить значения показателя политропы, параметры состояния (p,V,T) в точках 1, 2 и 3 nVT-цикла, и в точках 1^* , 2^*, 3^* SVT-цикла, а также смогли определить значения холодильных коэффициентов. Мы выяснили, что холодильные коэффициенты для nVT- и SVT-циклов больше холодильных коэффициентов цикла Карно.