Эксперимент со второй цепью с источником типа меандр (Хевисайд):
Построим переходную характеристику h(t) активного четырехполюсника, как реакцию цепи на единичное ступенчатое воздействие (на функцию Хевисайда, К = 50%, f = 1 Гц, Umax = 1 В и Umin = 0 В) к величине этого воздействия при нулевых начальных условиях:
А) Проводим измерения переходной характеристики h(t) при t = 0 мкс, получаем h(t) = 0:
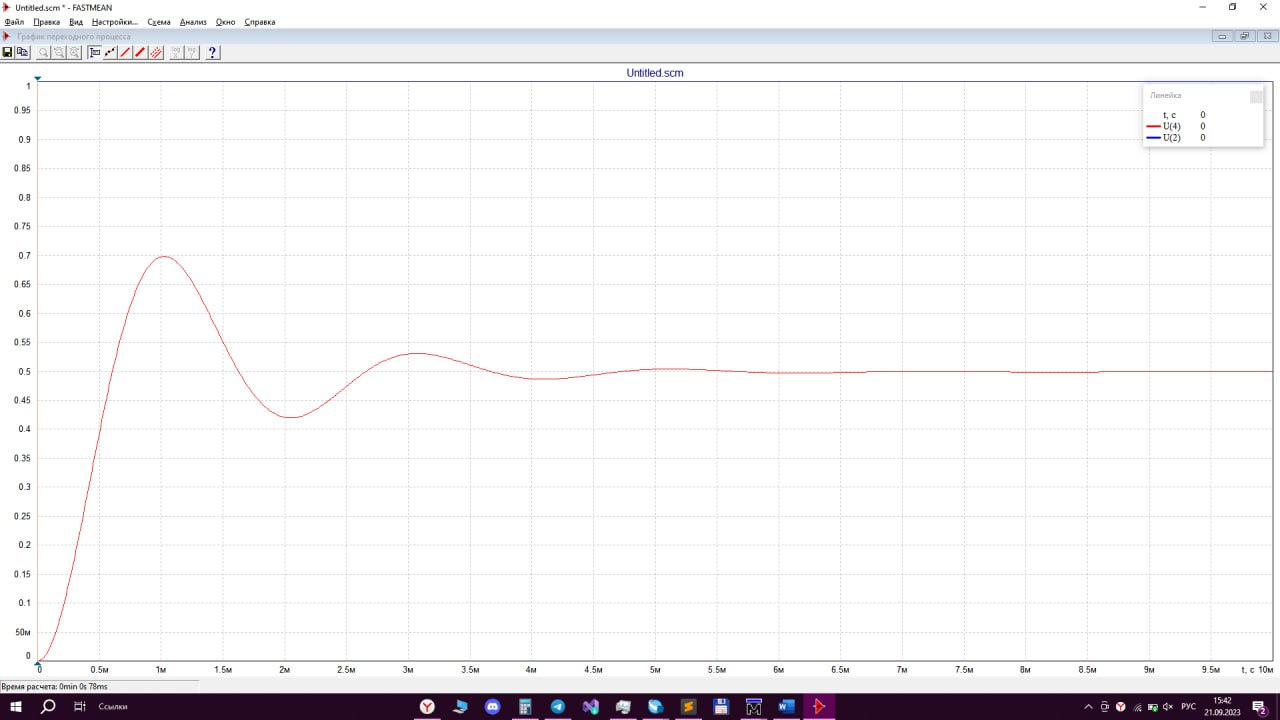
Б) Проводим измерения переходной характеристики h(t) при t → ∞, получаем, что она становится равна 0,498949449. h(t) =0,498949449 :
В) Проводим измерения переходной характеристики h(t) на первом минимуме (t ≈ 2.06691851 мс в данном случае), и получаем, что h(t) ≈ -0.419693228:
Г) Проводим измерения переходной характеристики h(t) на втором минимуме (t ≈ 4.07447383 мс в данном случае), и получаем, что h(t) ≈ 0.486373089
Таким образом, при w = 0 Гц и при w → ∞, амплитудно-частотные характеристики │H(jw)│принимают те же значения, что и переходная характеристика h(t) при t → ∞ и при t = 0 мкс соответственно.
Определим период колебаний, как разность t для большего и меньшего максимумов:
Th(t) = t2 – t1 = 1.65611299 мс - 0.541215654 мс = 1.114897336 мс.
Определим частоту колебаний, как величину, обратную периоду: wh(t) = 1/T = 1/1.114897336 мс ≈ 0.896943572928225 рад/мс.
Определим декремент затухания, как отношение h(t) для большего и меньшего максимумов:
Δh(t) = h(t2)/h(t1) = -0.8267778/ -0.2569178 ≈ 3.21806352.
Согласно таблице №6.2, варианту №1 соответствует следующий параметр коэффициента усиления K = -5,762.
Схема с измененным параметром K = -5,762:
При K, большем -5,762 (например, для К = -4,5) получаем возрастающую переходную характеристику с неустойчивой цепью:
Схема с измененным параметром K = -5:
При К, меньшем -5,762 (например, для К = -6.5) получаем аналогичную возрастающую переходную характеристику с неустойчивой цепью:
Схема с измененным параметром K = -6.5:
При K= -2,7 получаем быстро затухающую переходную характеристику с устойчивой цепью:
Схема с измененным параметром K = -2,7:
При K = 1,2 получаем мгновенно затухнувшую переходную характеристику с устойчивой цепью:
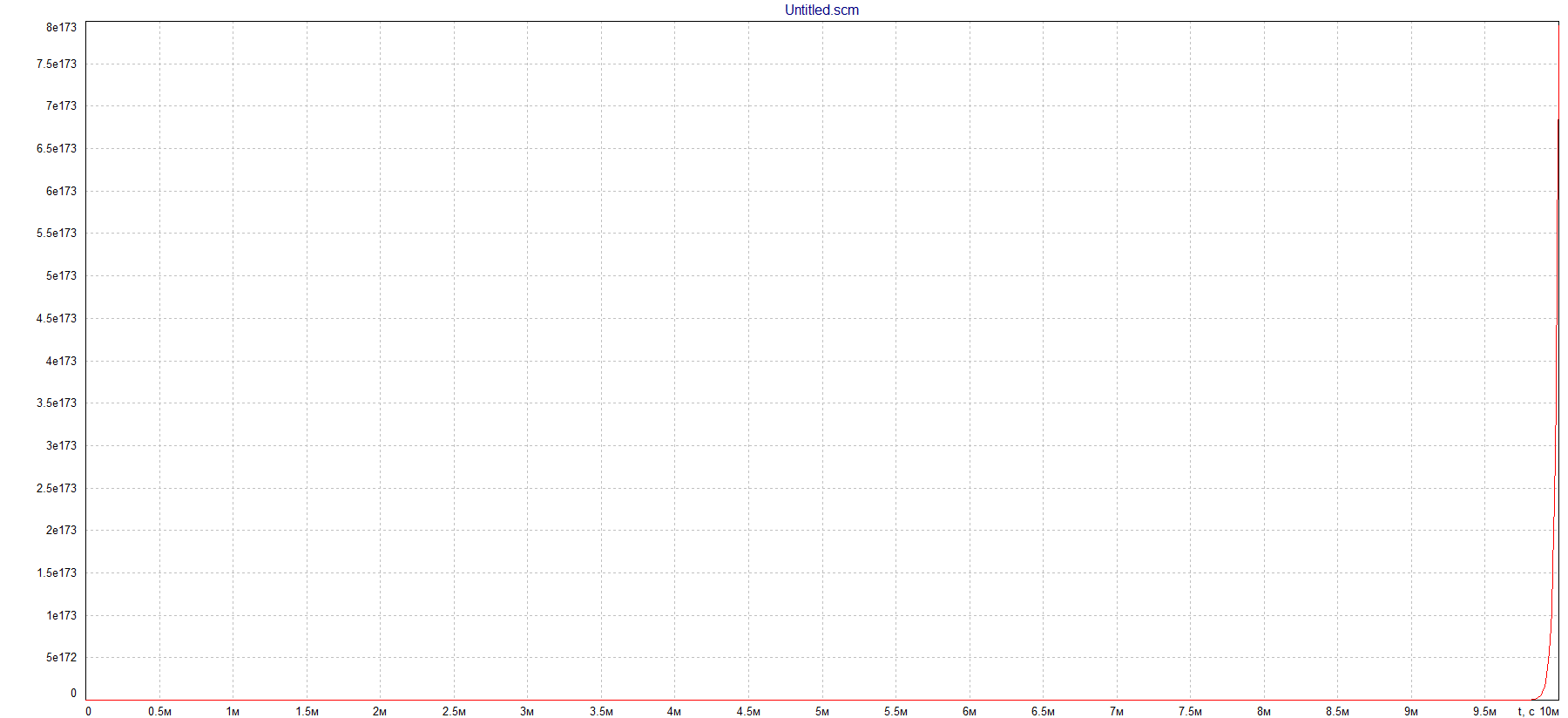
Схема с измененным параметром K = -1,2:
Схема второй исследуемой цепи с источником типа меандр (Дирак):
Согласно таблице №6.2, варианту №1 соответствует следующая схема ЭЦ со следующими параметрами (для источника типа меандр и функции Дирака):
Эксперимент со второй цепью с источником типа меандр (Дирак):
Построим импульсную характеристику g(t) активного четырехполюсника, как реакцию цепи на импульсное ступенчатое воздействие (на функцию Дирака, К = 0.01u%, f = 1 Гц, Umax = 10G В и Umin
= 0 В) к площади этого воздействия при нулевых начальных условиях:
А) Проводим измерения импульсной характеристики g(t) при t = 0 мкс, получаем g(t) = 0М:
Б)
Проводим
измерения
импульсной
характеристики g(t)
при t
→ ∞, получаем,
что она совпадает с импульсным ступенчатым
воздействием (функцией Дирака) и
становится равна 71,8453752. g(t) ≈ 71,8453752:
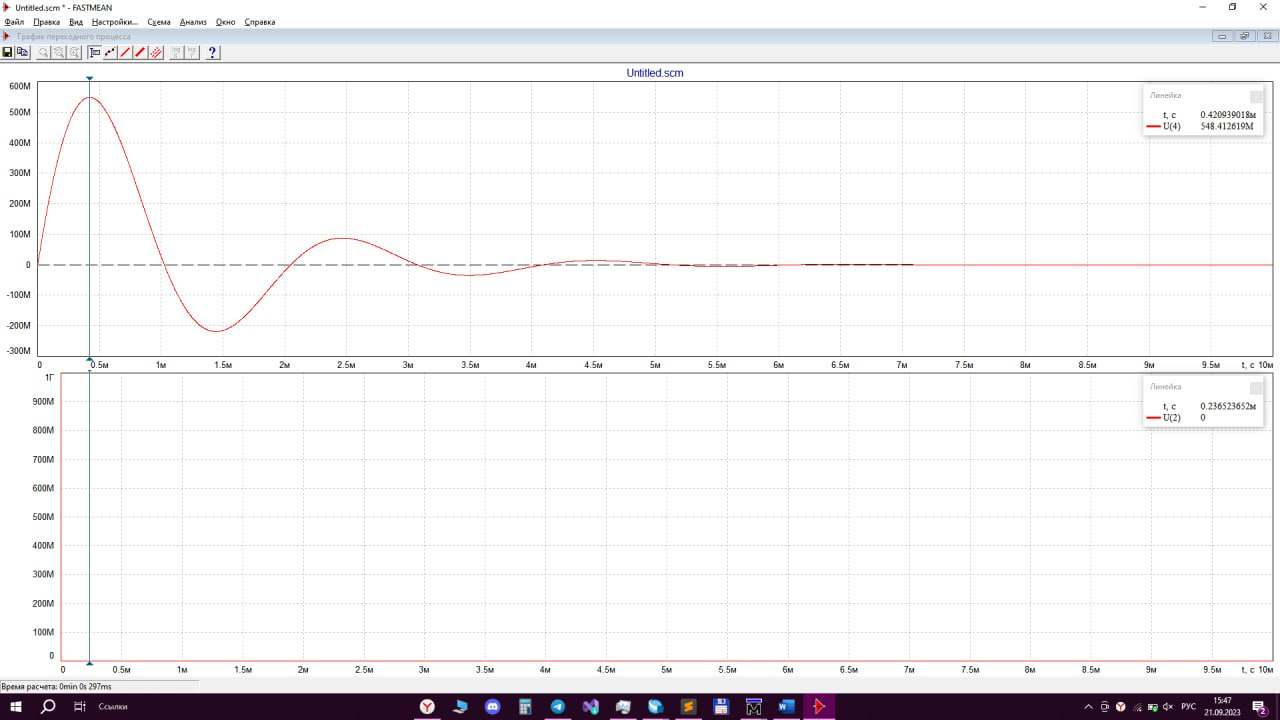
В) Проводим измерения импульсной характеристики g(t) на первом максимуме (t ≈ 0.42093901мс в данном случае), и получаем, что g(t) ≈548.412619М:
Г)
Проводим
измерения
импульсной
характеристики g(t)
на втором
максимуме (t ≈ 2.48246087 мс в данном
случае), и получаем, что g(t) ≈ 87.217946М:
Определим период колебаний, как разность t для большего и меньшего максимумов:
Tg(t) = t2 – t1 = 2.48246087 мс - 0.42093901 мс = 2,06146786 мс.
Определим частоту колебаний, как величину, обратную периоду: wg(t) = 1/T = 1/2,06146786 мс ≈ 0,48509124 рад/мс.
Определим декремент затухания, как отношение h(t) для большего и меньшего максимумов:
Δg(t) = h(t2)/h(t1) = 548.412619М /87.217946М ≈ 6,28784148.
Таким образом, можно заметить, что периоды и частоты колебаний переходной h(t) и импульсной g(t) характеристик будут примерно одинаковы:
А) Th(t) ≈ 2.061521782мс ≈ Tg(t) ≈ 2,06146786 мс.
Б) wh(t) ≈ 0,48432655 рад/мс ≈ fg(t) ≈ 0,48509124 рад/мс.