ФЕДЕРАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ

ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Отчет по лабораторной работе №6

Предмет: Теория электрической цепи.

Тема: Анализ частотных и временных характеристик пассивного и активного четырехполюсников с использованием программы FASTMEAN.

Бригада №1

Студенты группы

Старший преподаватель:

Кубалова А.Р.

Санкт-Петербург 2023

Оглавление:

Оглавление. 2

Цели. 2

Схема первой исследуемой цепи с гармоническим источником. 2

Эксперимент с первой цепью с гармоническим источником. 3

Схема первой исследуемой цепи с источником типа меандр (Хевисайд). 4

Эксперимент с первой цепью с источником типа меандр (Хевисайд). 5

Схема первой исследуемой цепи с источником типа меандр (Дирак). 7

Эксперимент с первой цепью с источником типа меандр (Дирак). 7

Предварительный расчет для первой цепи 10

Схема второй исследуемой цепи с гармоническим источником. 11

Эксперимент со второй цепью с гармоническим источником. 11

Схема второй исследуемой цепи с источником типа меандр (Хевисайд). 13

Эксперимент со второй цепью с источником типа меандр (Хевисайд). 14

Схема второй исследуемой цепи с источником типа меандр (Дирак). 20

Эксперимент со второй цепью с источником типа меандр (Дирак). 20

Предварительный расчет для второй цепи 22

Выводы 26

Цели:

1. Исследовать частотные характеристики пассивного и активного четырехполюсников: амплитудно-частотную │H(jw)│ и фазо- частотную θ(jw).

2. Исследовать временные характеристики пассивного и активного четырехполюсников: переходную h(t) и импульсивную g(t) характеристики.

3. Оценить связь между временными и частотными характеристиками исследуемого четырехполюсника.

Схема первой исследуемой цепи с гармоническим источником:

1. Согласно таблице №6.1, варианту №1 соответствует следующая схема ЭЦ со следующими параметрами (для гармонического источника):

Эксперимент с первой цепью с гармоническим источником:

2. Проведем символьный анализ данной схемы, получим следующее выражение для операторно-передаточной функции H(P):

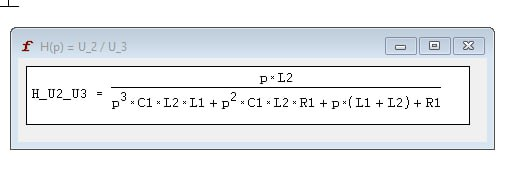
3. Подаем на вход гармонические колебания с конечной частотой 10MГц и получаем частотные характеристики пассивного четырехполюсника:

А) Проводим измерения частотных характеристик │H(jw)│пассивного четырехполюсника при f = 0 Гц, получаем │H(jw)│= 0:

Б) Проводим измерения частотных характеристик │H(jw)│пассивного четырехполюсника при f → ∞, получаем │H(jw)│= 1:

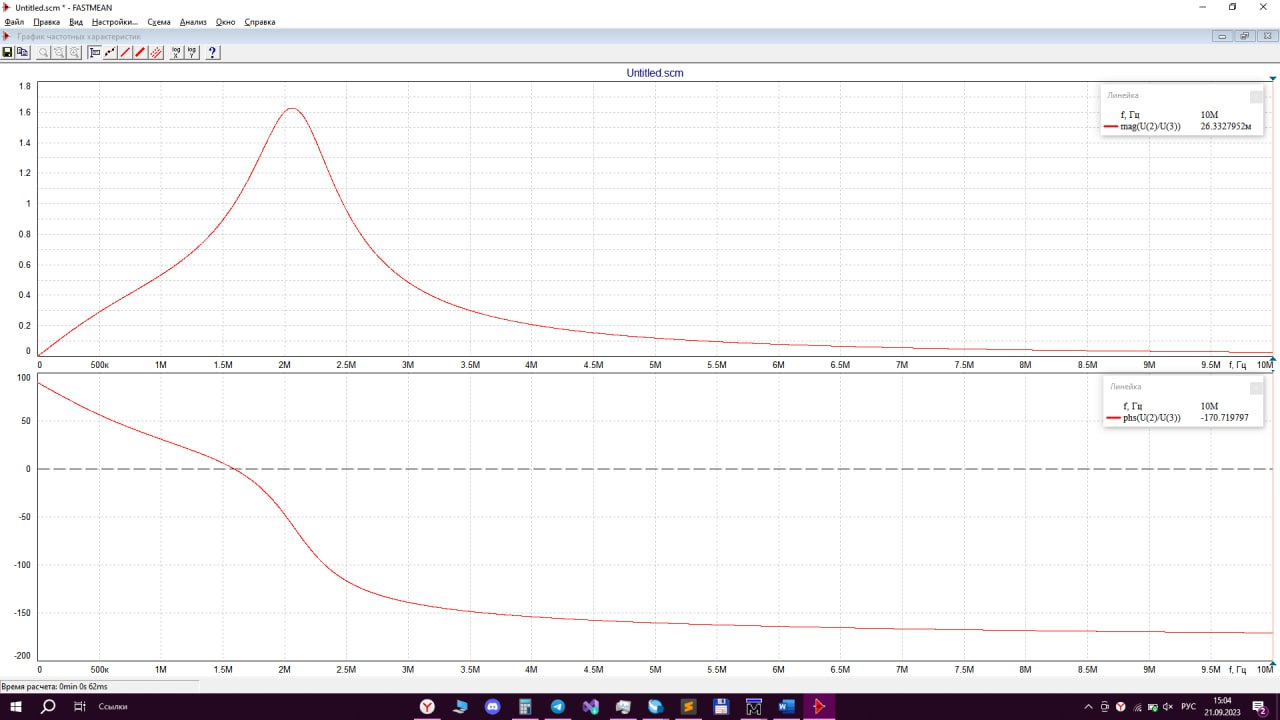
В) Проводим измерения частотных характеристик│H(jw)│пассивного четырехполюсника на квазирезонансной частоте (f ≈ 2,06152186 MГц), получаем, что │H(jw)│= 1,62729217:

Г) Фиксируем отношение │H(jw)│ (полученного в пункте А) к √2, получаем │H(jw)│ ≈ 1,15313011 (граничная частота полосы пропускания). В связи с неточностью предлагаемых графиком измерений получаем: 0.81538612.

Схема первой исследуемой цепи с источником типа меандр (Хевисайд):

4. Согласно таблице №6.1, варианту №1 соответствует следующая схема ЭЦ со следующими параметрами (для источника типа меандр и функции Хевисайда):

Эксперимент с первой цепью с источником типа меандр (Хевисайд):

5. Построим переходную характеристику h(t) пассивного четырехполюсника, как реакцию цепи на единичное ступенчатое воздействие (на функцию Хевисайда, К = 50%, f = 1 Гц, Umax = 1 В и Umin = 0 В) к величине этого воздействия при нулевых начальных условиях:

А) Проводим измерения переходной характеристики при t = 0 мкс, получаем h(t) = 0:

Б) Проводим измерения переходной характеристики h(t) при t → ∞, получаем 0.144887013н. h(t) ≈ 0.144887013н ≈ 0:

В) Проводим измерения переходной характеристики h(t) на первом максимуме (t ≈ 0.194279547 мкс в данном случае), и получаем, что h(t) ≈ 0.531236408:

Г) Проводим измерения переходной характеристики h(t) на втором максимуме (t ≈ 0.690771722 мкс в данном случае), и получаем, что h(t) ≈ 0.13755454:

6. Таким образом, при f = 0 Гц и при f → ∞, амплитудно-частотные характеристики │H(jw)│принимают те же значения, что и переходная характеристика h(t) при t → ∞ и при t = 0 мкс соответственно.

7. Определим период колебаний, как разность t для большего и меньшего максимумов:

Th(t) = t2 – t1 = 0.690771722 мкс - 0.194279547мкс = 0.496492175 мкс.

8. Определим частоту колебаний, как величину, обратную периоду: wh(t) = 1/T = 1/0.949208996 мкс ≈ 2.01413043 рад/мкс.

9. Определим декремент затухания, как отношение h(t) для большего и меньшего максимумов:

Δh(t) = h(t2)/h(t1) =0.531236408 / 0.13755454 ≈3.86200563.

Схема первой исследуемой цепи с источником типа меандр (Дирак):

10. Согласно таблице №6.1, варианту №1 соответствует следующая схема ЭЦ со следующими параметрами (для источника типа меандр и функции Дирака):