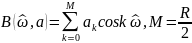lr_03 / Шаблон отчёта
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное образовательное
бюджетное учреждение высшего образования
«Санкт-Петербургский государственный университет телекоммуникаций
им. проф. М. А. Бонч-Бруевича»
______________________________________________________________________
Кафедра радиосистем и обработки сигналов
Дисциплина «Цифровая обработка сигналов»
Отчет по лабораторной работе № 3
«Синтез КИХ-фильтра»
Выполнили
студенты гр.
Принял
ассистент каф. РОС
_____________ Бойко И.А.
Санкт-Петербург
2024
Входные данные
Табл. 1. Типы избирательности КИХ-фильтра
|
6 |
Тип избирательности КИХ-фильтра |
чётный |
+ |
ФНЧ и РФ |
нечётный |
|
ФВЧ и ПФ |
Табл. 2.1. Требования к АЧХ ФНЧ
Частоты (Гц) и их идентификаторы |
Максимально допустимые отклонения АЧХ |
|||||
Граничная частота в ПП |
|
|
В ПП |
|
0.05 |
|
Граничная частота в ПЗ |
|
|
В ПЗ |
|
0.01 |
|
Табл. 2.2. Требования к АЧХ РФ
Частоты (Гц) и их идентификаторы |
Максимально допустимые отклонения АЧХ |
|||||
Граничная частота ПП1 |
|
|
В ПП1 |
|
0.05 |
|
Левая граничная частота ПЗ |
|
|
В ПЗ |
|
0.01 |
|
Правая граничная частота ПЗ |
|
|
||||
Граничная частота ПП2 |
|
|
В ПП2 |
|
0.05 |
|
Синтез КИХ-фильтра ФНЧ методом окна Кайзера.
Тип (по избирательности) |
Порядок Rmin/Ropt =1,4 |
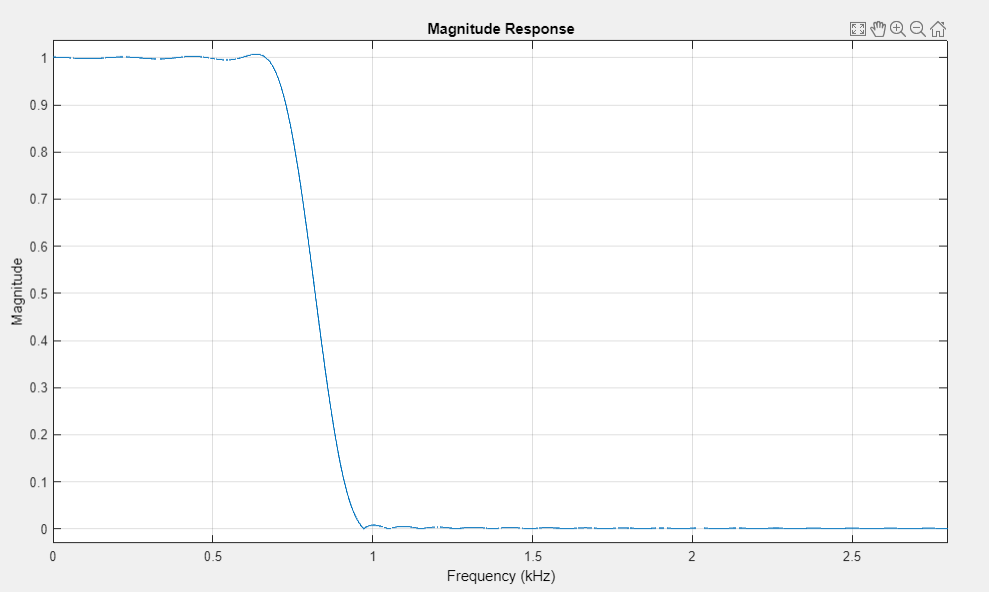
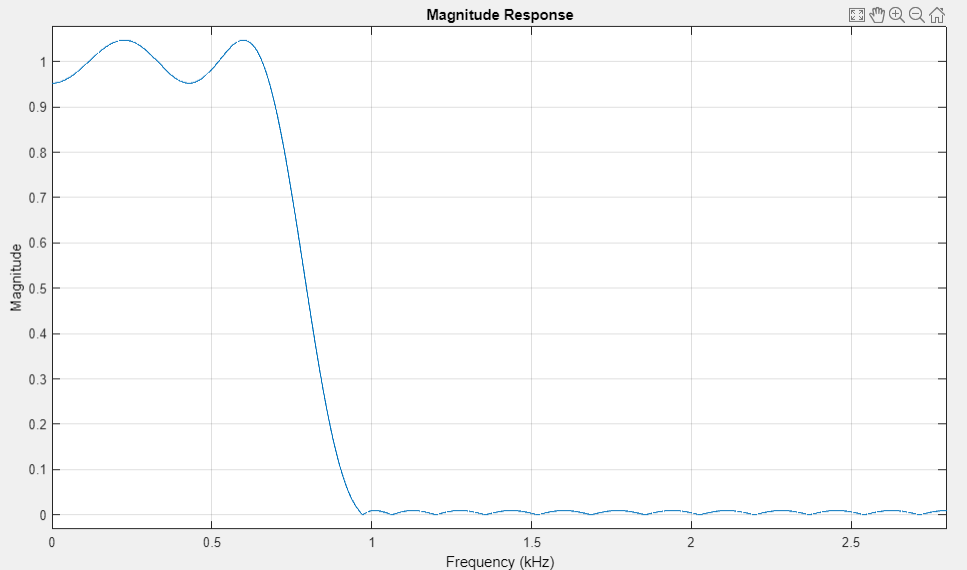
график АЧХ Rmin=45 |
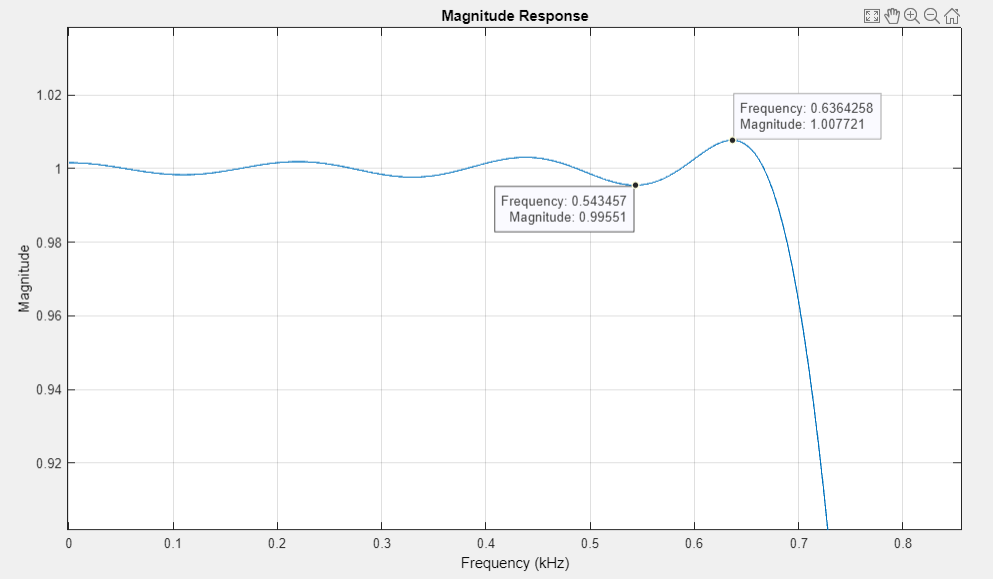
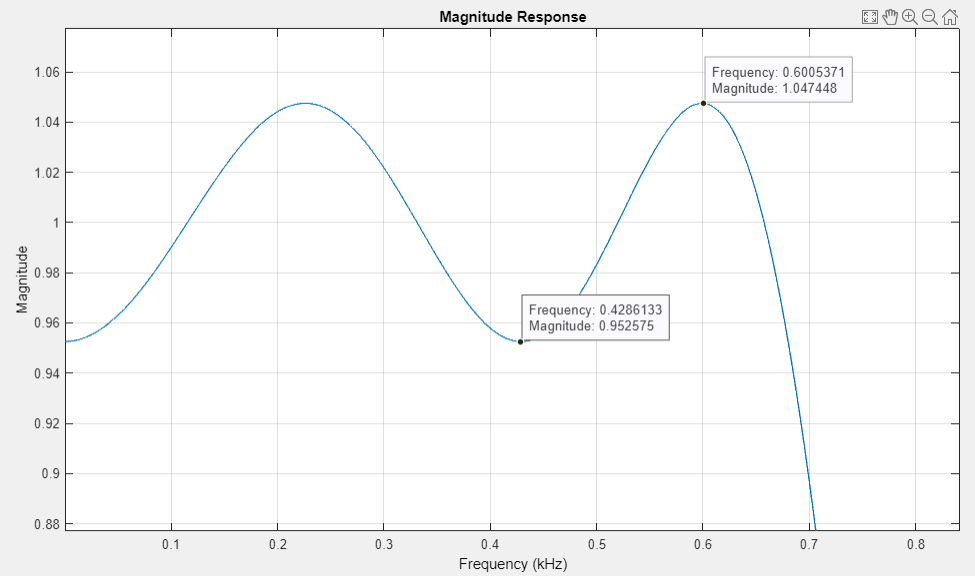
график АЧХ в ПП (приближенный) |
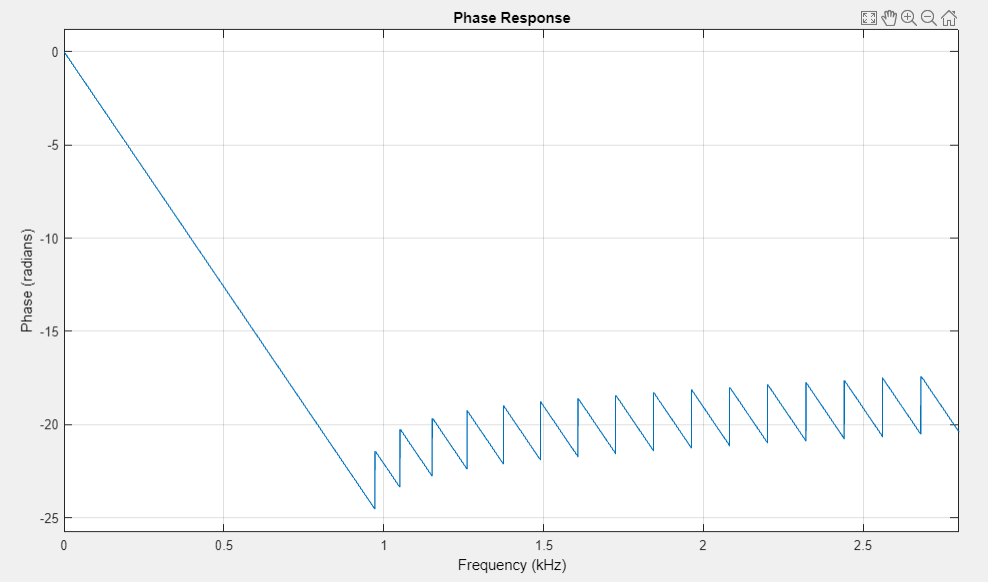
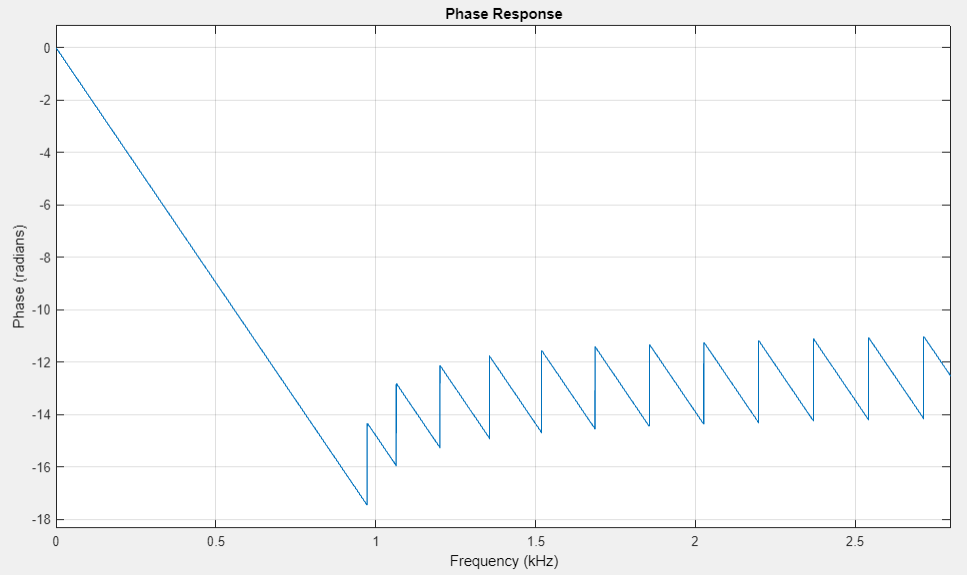
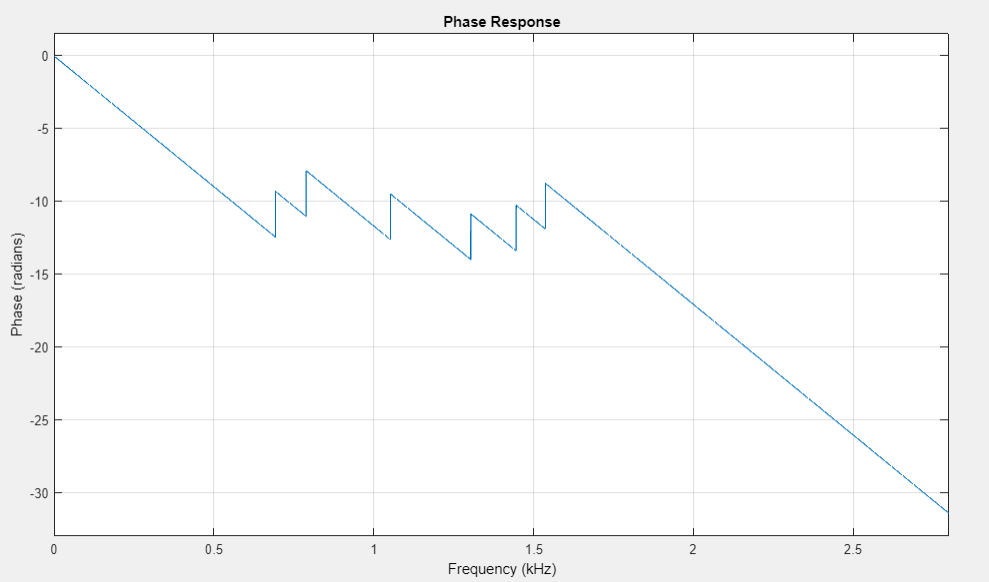
график ФЧХ |
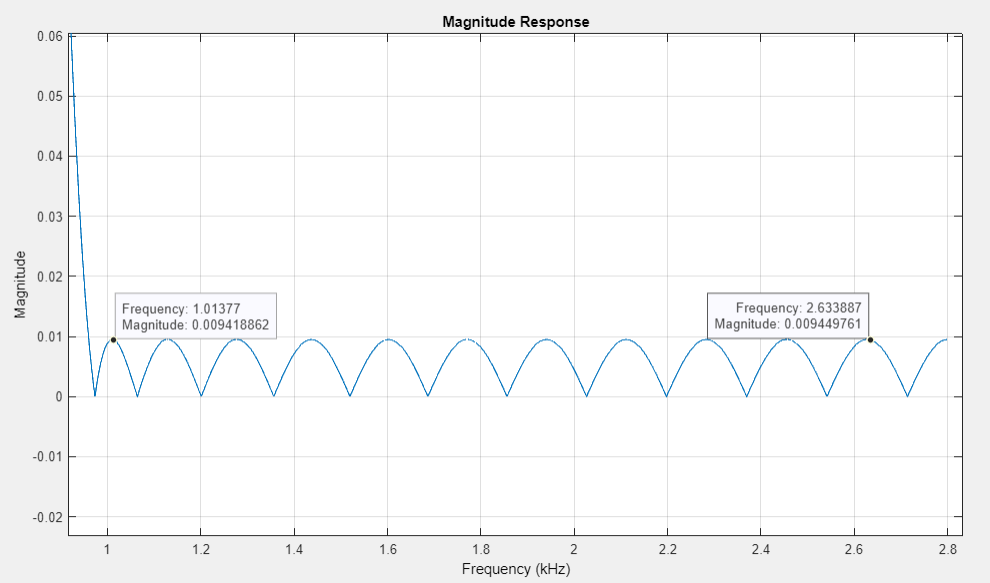
график АЧХ в ПЗ (приближенный) |
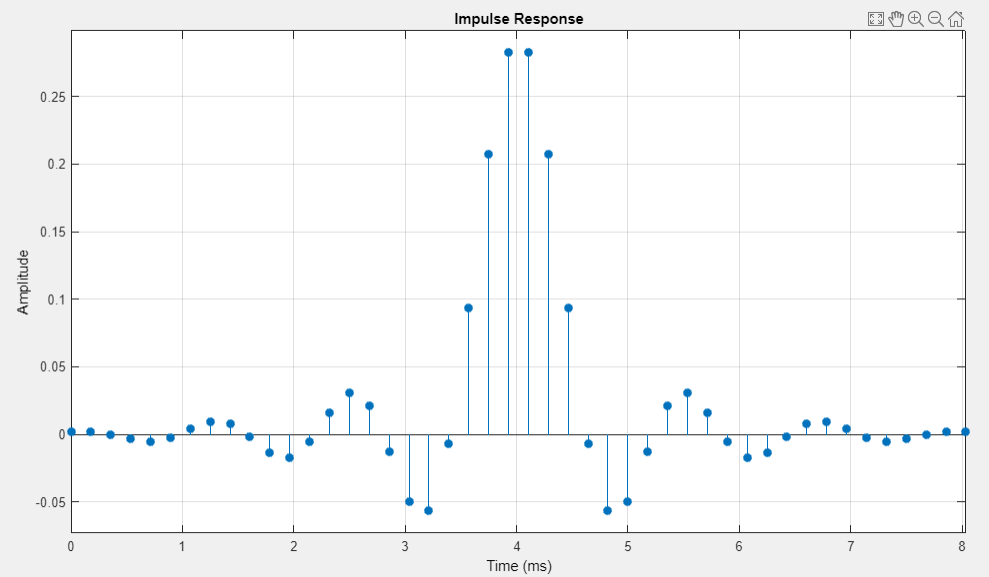
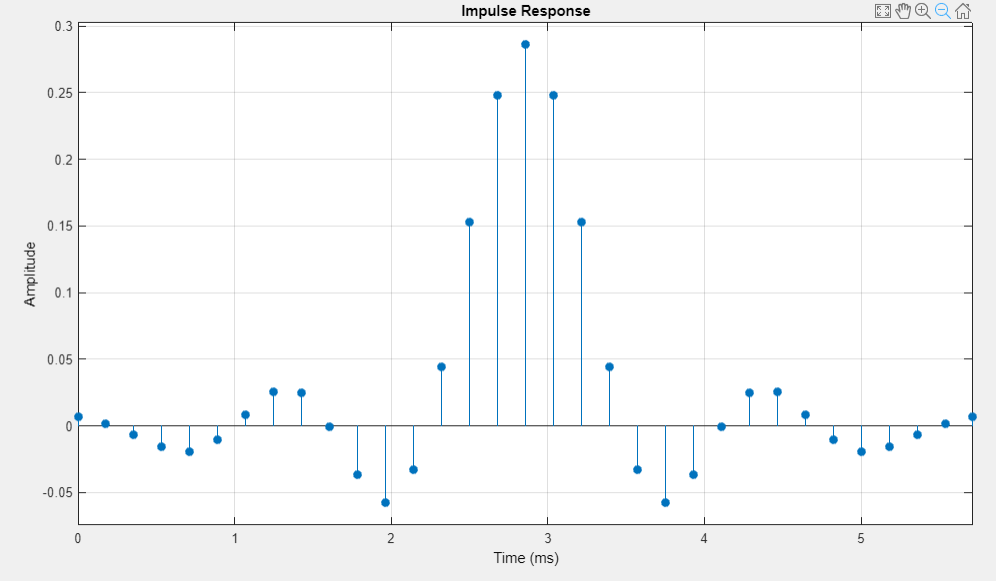
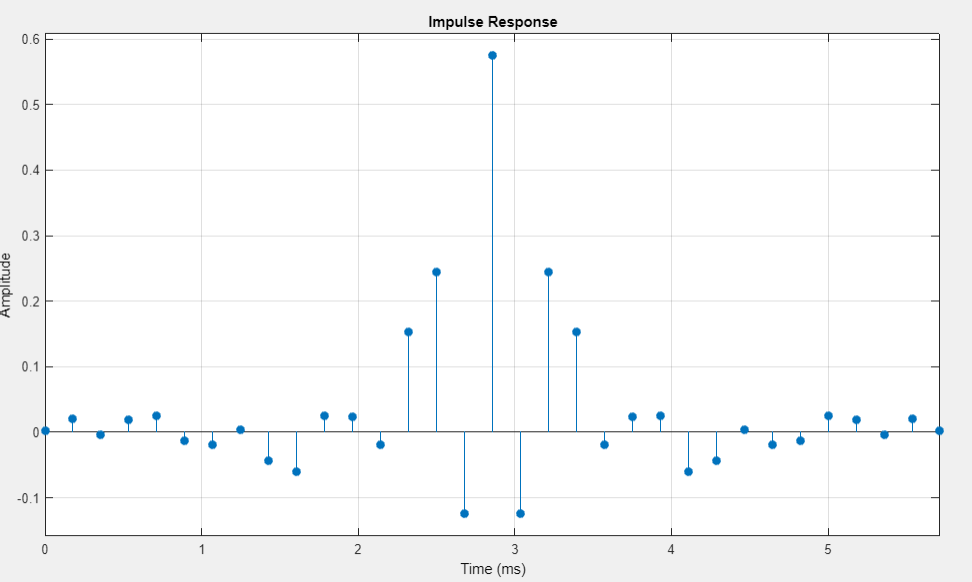
график ИХ (симметричная) |
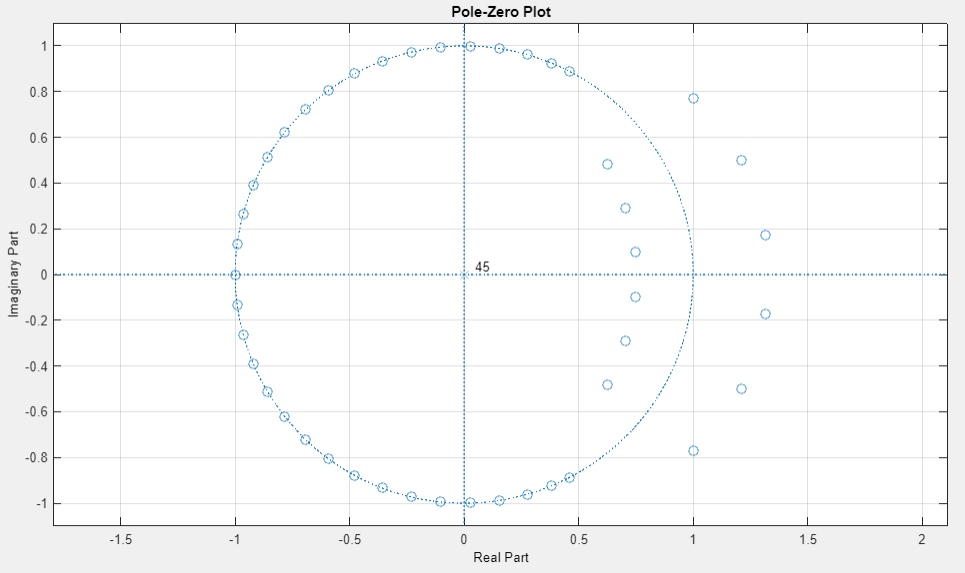
карта нулей и полюсов |
АЧХ в ПП и ПЗ неравноволновые, отклонения соответствуют требованиям.
ФЧХ является линейной с точностью до скачков на 𝜋.
Полюс на карте находится внутри единичной окружности, следовательно выполняется второй критерий устойчивости. Часть нулей находится внутри единичной окружности, часть на ней и часть вне.
Синтез КИХ-фильтра РФ методом окна Кайзера.
Тип (по избирательности) |
Порядок Rmin/Ropt = 1,43 |
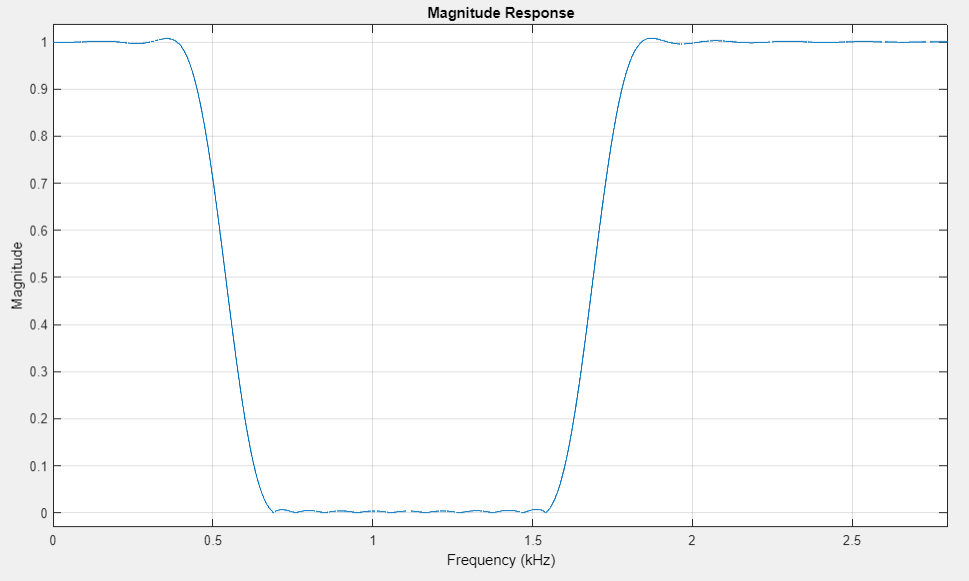
график АЧХ Rmin=46 |
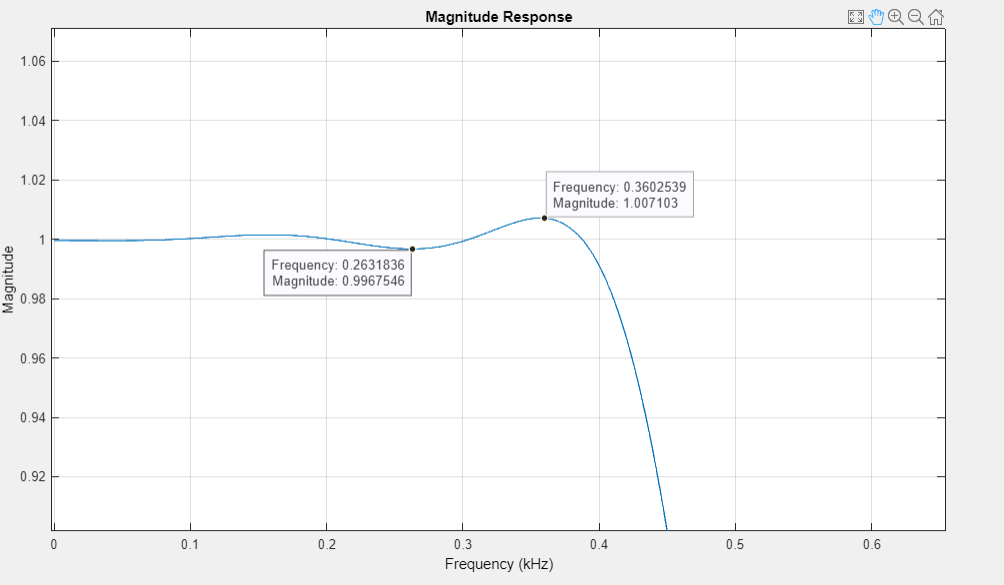
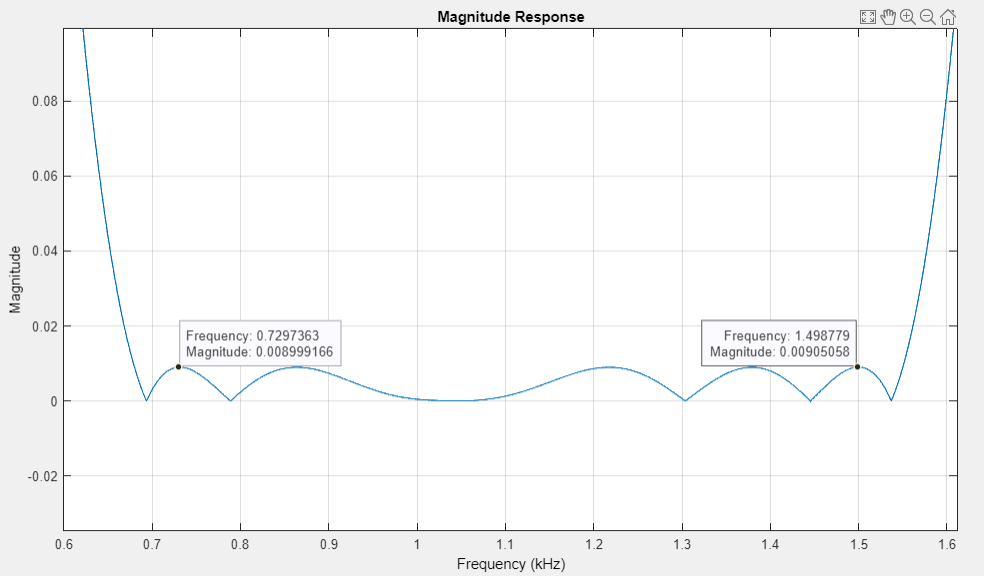
график АЧХ в ПП1 (приближенный) |
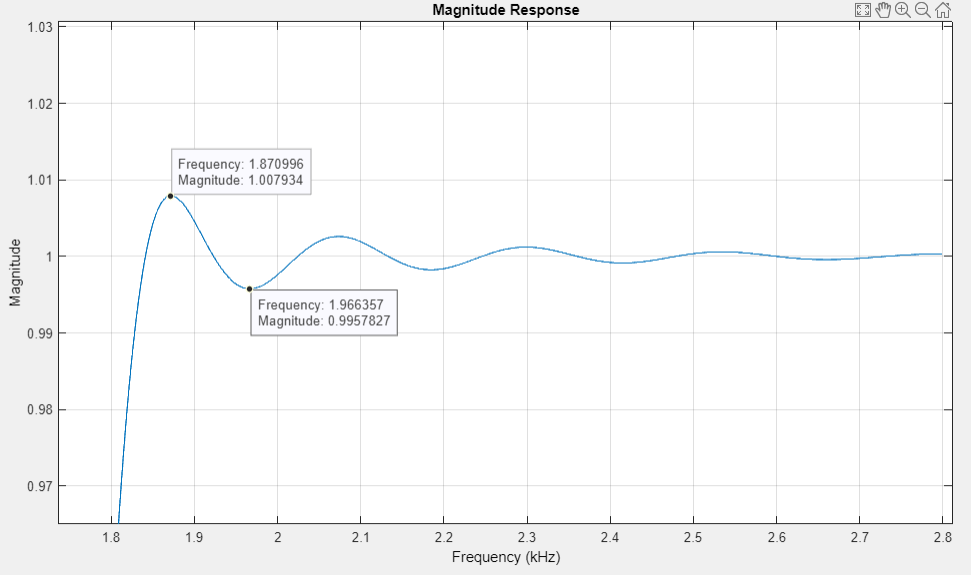
график АЧХ в ПП2 (приближенный) |
|
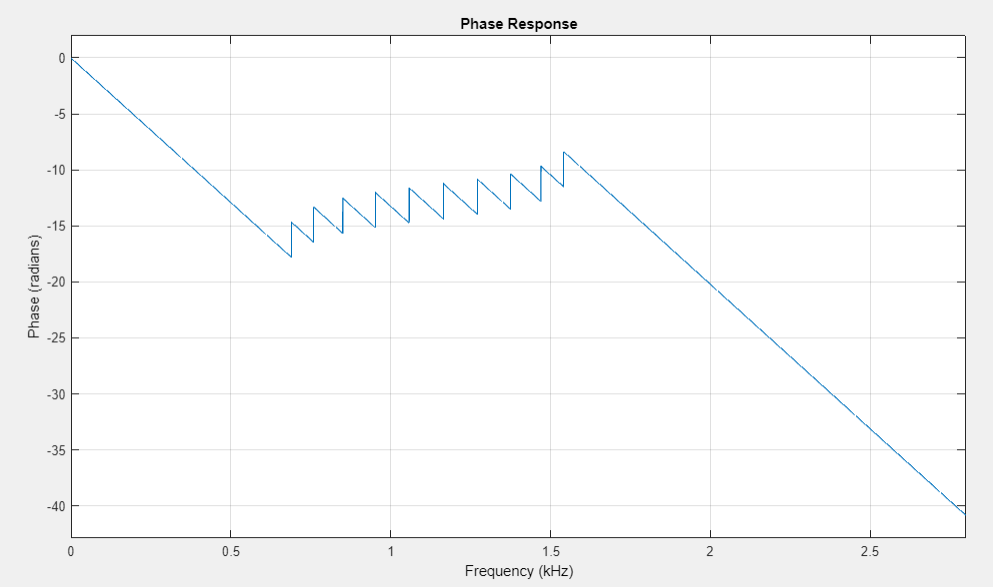
график ФЧХ |
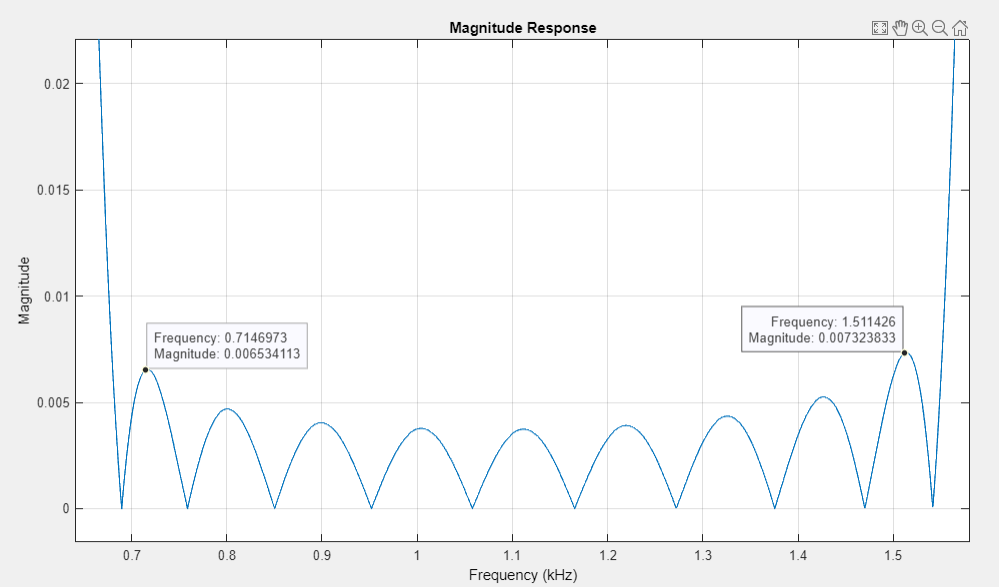
график АЧХ в ПЗ (приближенный) |
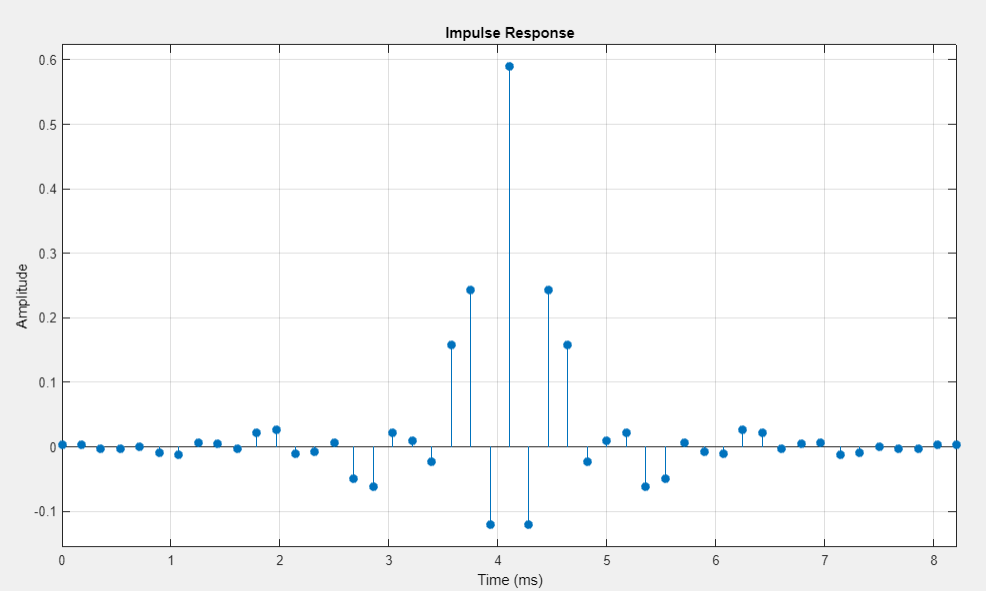
график ИХ (симметричная) |
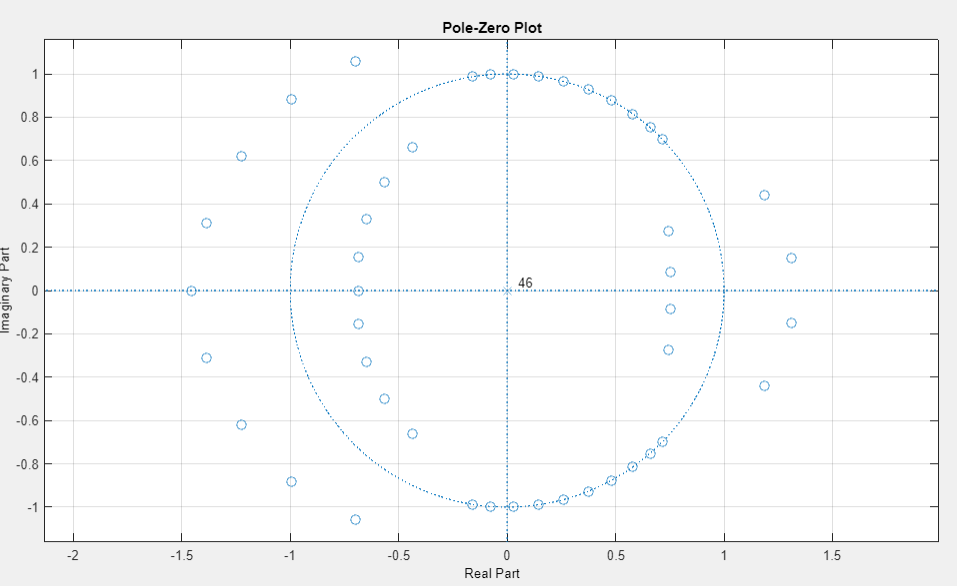
карта нулей и полюсов |
АЧХ в ПП и ПЗ неравноволновые, отклонения соответствуют требованиям.
ФЧХ является линейной с точностью до скачков на 𝜋.
Полюс на карте находится внутри единичной окружности, следовательно выполняется второй критерий устойчивости. Часть нулей находится внутри единичной окружности, часть на ней и часть вне.
Синтез КИХ-фильтра ФНЧ методом Чебышева.
Тип (по избирательности) |
Порядок Rmin/Ropt = 1,4 |
график АЧХ Ropt=32 |
график АЧХ в ПП (приближенный)
|
график ФЧХ |
график АЧХ в ПЗ (приближенный) |
график ИХ (симметричная) |
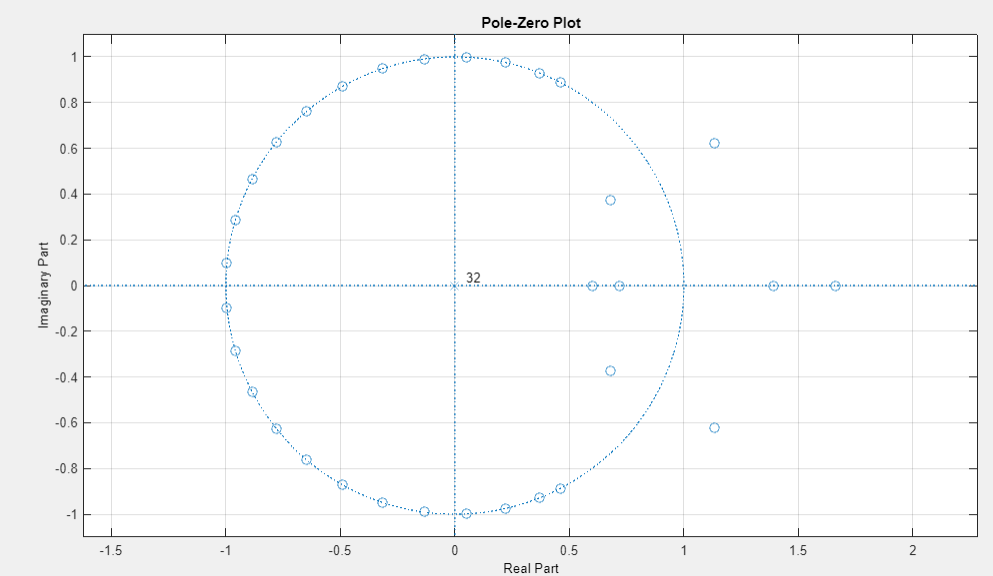
карта нулей и полюсов |
АЧХ в ПП и ПЗ равноволновые, отклонения соответствуют требованиям.
ФЧХ является линейной с точностью до скачков на 𝜋.
Полюс на карте находится внутри единичной окружности, следовательно выполняется второй критерий устойчивости. Часть нулей находится внутри единичной окружности, часть на ней и часть вне.
Синтез КИХ-фильтра РФ методом Чебышева.
Тип (по избирательности) |
Порядок Rmin/Ropt = 1,43 |
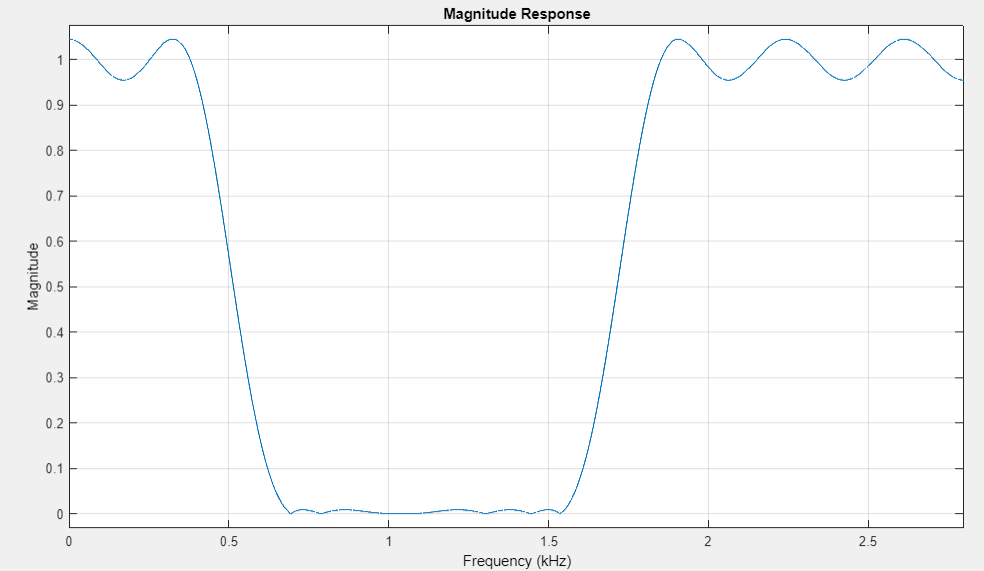
график АЧХ Ropt=32 |
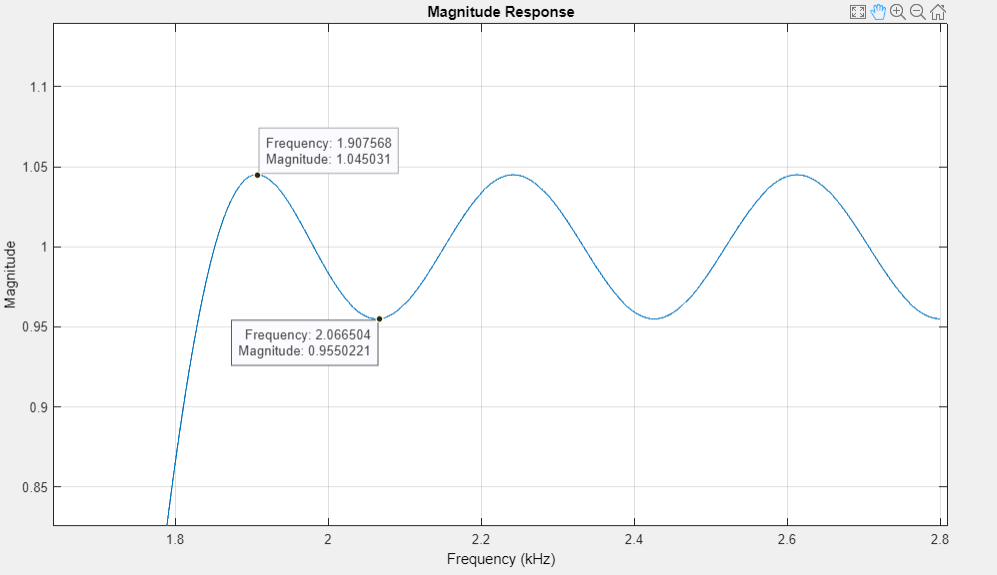
график АЧХ в ПП1 (приближенный) |
график АЧХ в ПП2 (приближенный) |
|
график ФЧХ |
график АЧХ в ПЗ (приближенный) |
график ИХ (симметричная) |
карта нулей и полюсов |
АЧХ в ПП и ПЗ равноволновые, отклонения соответствуют требованиям.
ФЧХ является линейной с точностью до скачков на 𝜋.
Полюс на карте находится внутри единичной окружности, следовательно выполняется второй критерий устойчивости. Часть нулей находится внутри единичной окружности, часть на ней и часть вне.
Добавить таблицу:
Тип КИХ-фильтра |
Амплитудная функция |
ЛФЧХ |
Тип избирательности |
1 ИХ- симметричная R - чётный |
|
|
ФНЧ ФВЧ ПФ РФ |
2 ИХ-симметричная R -нечетная |
|
|
ФНЧ ПФ |
3 ИХ – антисимметричная R- четная |
|
|
ПФ |
4 ИХ – антисимметричная R- нечетная |
|
|
ФВЧ ПФ |
Добавить таблицу
Метод синтеза |
Метод окон |
Метод чебышёвской аппроксимации |
R |
45
|
32 |
Преимущества |
Простота подсчета вектора a, возможность синтеза фильтра в реальном времени |
Оптимальность синтезируемого КИХ фильтр |
Недостатки |
Не возможность синтезировать оптимальный КИХ фильтр. |
Сложность подсчета вектора a, не возможность синтеза фильтра в реальном времени. |
Метод синтеза |
Метод окон |
Метод чебышёвской аппроксимации |
R |
|
|
Преимущества |
1. Гибкость настройки: выбор определенного окна позволяет настраивать амплитудно-частотную характеристику фильтра на требуемые параметры. 2. Легкость в реализации: метод окон относительно прост в реализации, что делает его доступным для широкого круга специалистов. 3. Возможность управления спектральными характеристиками: метод окон позволяет более точно управлять спектральными свойствами фильтра, обеспечивая оптимальное соотношение между разрешением и подавлением нежелательных компонентов. |
1. Наилучшее приближение: метод чебышевской аппроксимации позволяет получить фильтр с минимальными отклонениями от желаемой частотной характеристики в заданном диапазоне частот. 2. Быстродействие: использование метода чебышевской аппроксимации позволяет достичь требуемых характеристик фильтра за минимальное количество итераций. 3. Настройка параметров: данный метод позволяет настраивать параметры фильтра, такие как порядок, полоса пропускания, полоса подавления и др., для получения оптимального решения. |
Недостатки |
1. Лобовые лепестки: при использовании некоторых окон могут возникать лобовые лепестки (побочные лопья) в спектре фильтра, что может привести к искажениям сигнала. 2. Широкая полоса перехода: некоторые окна могут привести к увеличению ширины полосы перехода фильтра, что может усложнить его настройку на желаемые частотные характеристики. 3. Ресурсоемкость: в случае использования сложных окон, метод окон может потребовать дополнительных вычислительных ресурсов для реализации фильтра. |
1. Осцилляции в полосах перехода: при использовании метода чебышевской аппроксимации, особенно при высоких степенях фильтра, могут возникать осцилляции (колебания) в полосах перехода, что может привести к нежелательным эффектам. 2. Сложность настройки: выбор оптимального коэффициента ряда Чебышёва требует определенных знаний и опыта, так как слишком большие значения могут привести к нежелательным эффектам. 3. Неоднородные отклонения: при использовании метода чебышевской аппроксимации, отклонения в полосе пропускания и в полосе подавления могут быть неоднородными, что усложняет настройку фильтра. |



 680
680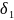

 960
960

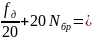 400
400
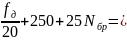 680
680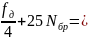 1550
1550 1830
1830