lr_7 / lr1

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное образовательное

бюджетное учреждение высшего образования

«Санкт-Петербургский государственный университет телекоммуникаций

им. проф. М. А. Бонч-Бруевича»

______________________________________________________________________

Кафедра радиосистем и обработки сигналов

Дисциплина «Цифровая обработка сигналов»

Отчет по лабораторной работе № 1

«Дискретные сигналы»

Выполнили

студенты гр.

Принял

ассистент каф. РОС

_____________ Бойко И.А.

Санкт-Петербург

2024

Входные данные

Таблица 1 Таблица исходных данных

Переменная	Назначение	Значение
	Номер бригады
	Длина последовательности
	Период дискретизации
	Основание экспоненты
	Амплитуда гармонического сигнала
	Частота гармонического сигнала
	Задержка
	Амплитуда импульса
	Начальный момент импульса
	Длина импульса
	Амплитуды гармонических сигналов
	Частоты гармонических сигналов
	Коэффициенты линейной комбинации сигналов
	Математическое ожидание	4
	Дисперсия	6

1. Цифровой единичный импульс

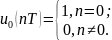
Для каждого сигнала/функции должна быть приведена формула.

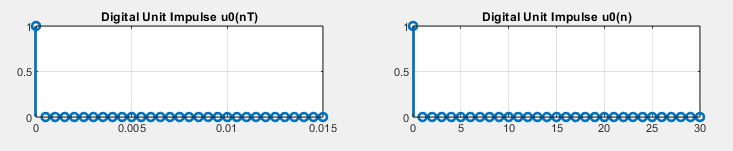
Рис. 1

Все графики должны быть подписаны (оси, единицы измерения, длина/ длительность сигнала, период для периодических сигналов).

Все значения, выводимые в Command Window, должны быть в отчёте.

Пояснить:

• взаимосвязь между дискретным и дискретным нормированным временем

Ответ

Взаимосвязь между дискретным и дискретным нормированным временем.

Значения 𝑛𝑇, где 𝑇 = 1/𝑓д – период дискретизации.

Значение n: 𝑛 = 𝑛𝑇/T

• различие между цифровым единичным импульсом и дельта-функцией

Ответ

Различие между цифровым единичным импульсом и дельта-функцией.

Цифровой единичный импульс. Это аналог дельта-функции для дискретных систем, но в отличие него, - физически реализуемый сигнал.

Дельта-функция (она же функция Дирака), используется в аналоговых системах.

На каждое пояснение должен быть дан ответ. В случае затруднений, оставить пустое место после пояснения. Удалять пояснения запрещается!

2. Цифровой единичный скачок

Рис.2

Соответствие между цифровым и аналоговым единичными скачками:

Функция единичного скачка (она же функция Хевисайда, или функция включения), используется в аналоговых системах

Чему равна частота дискретизации цифрового единичного скачка.

3. Дискретная экспонента

Рис.3

Соответствие между дискретной и аналоговой экспонентами.

Вид дискретной экспоненты определяется величиной и знаком параметра a.

Формула дискретной экспоненты в общем виде и со своими исходными данными.

4. Дискретный комплексный гармонический сигнал

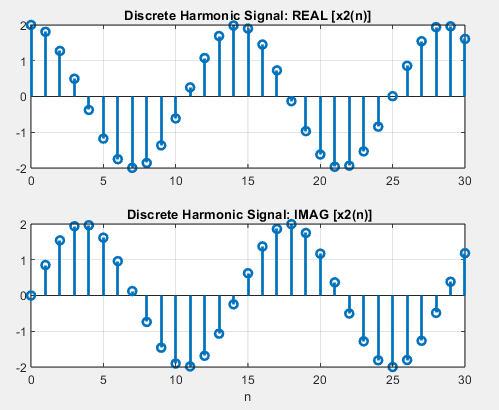
Рис. 4

Сигнал в виде комбинации двух вещественных последовательностей.

5. Задержанный последовательности

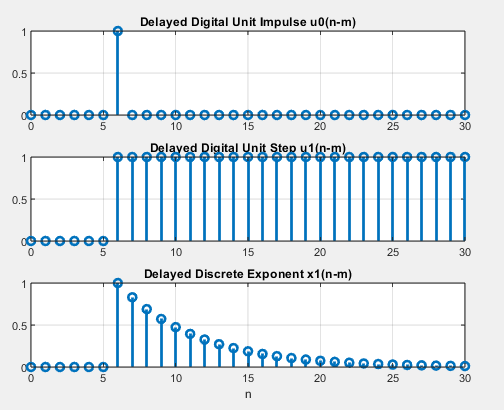
Рис. 5

Формула задержанных последовательностей.

6. Дискретный прямоугольный импульс

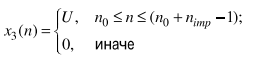
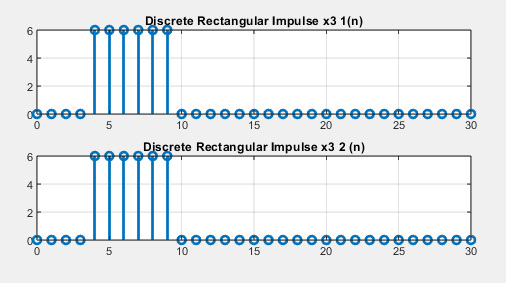
Рис.6

y = rectpuls(t,w)  генерирует прямоугольник модульной высоты в шагах расчета, обозначенных в массиве t, сосредоточенный о t= 0, ширины w.

В первом случае график был получен при помощи специальной функции rectpuls.

Во втором случае график был получен путем создания массива матриц.

7. Дискретный треугольный импульс

Рис. 7

x ₄(n) формируется посредством свёртки дискретного прямоугольного импульса x₃(n) c самим собой, на интервале времени

Длина свёртки L = 61.

Аналитическая запись свёртки:

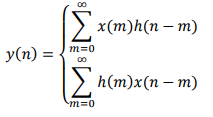
8. Линейная комбинация дискретных гармонических сигналов

где

На интервале времени

Рис. 8

Для моделирования линейной комбинации сигналов были созданы матрица дискретных гармоник и матрица коэффициентов, после эти матрицы были перемножены и просуммированы. Итоговая матрица была транспонирована.

Среднее значение вычисляется путем сложения всех значений функции и делением их на число значений.

Энергия вычисляется возведением в квадрат всех значений матрицы исходных значений и дальнейшей их суммой.

Мощность определяется делением энергии на длину матрицы исходных значений.

9. Дискретный гармонический сигнал с экспоненциальной огибающей

Рис. 9

Для моделирования дискретного сигнала задается дискретное нормированное время (интервал значений), далее создаем дискретный гармонический сигнал, который в дальнейшем умножаем на экспоненциальную огибающую .

10. Периодическая последовательность дискретных прямоугольных импульсов

Рис. 10

В процессе моделирования вычисляется период последовательности, задается число периодов. На основе этого создается периодическая последовательность и задается дискретное нормированное время.

11. Равномерный белый шум

+ отметить на графике значение автоковариационной функции при нулевом временном сдвиге. Чему будет равно значение автоковариационной функции при нулевом временном сдвиге? (см. п. 14)

Рис. 11

Длина оценки автоковариационной функции: L=2N-1=19999

12. Нормальный белый шум

+ отметить на графике значение АКФ при нулевом временном сдвиге. Чему будет равно значение АКФ при нулевом временном сдвиге? (см. п. 14)

Рис.12

Длина оценки АКФ: L=2N-1=19999

13. Аддитивная смесь

Рис. 13

Аддитивная смесь сигнала с шумом – суммируется шум с полезным сигналом.

13. Оценка АКФ

Рис. 14

Var_x8 = 3.6372

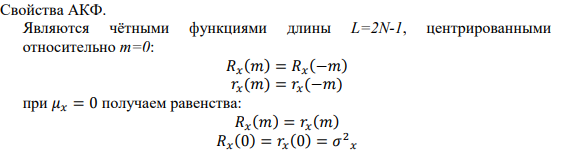
13. Нормальный белый шум

+ отметить на гистограммах значение мат. ожидания и СКО.

Рис. 15

Рис. 16

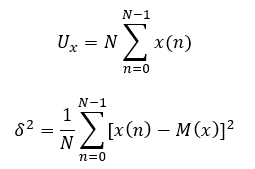
При изменении мат. ожидания производимый шум сдвигается по оси ординат.

При изменении дисперсии изменяется размах сигнала.

Гистограмма отображает количество значений определенной амплитуды

При изменении мат ожидания гистограмма сдвигается по оси абсцисс.

При изменении дисперсии изменяется ширина гистограммы.