lab2

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное образовательное

бюджетное учреждение высшего образования

«Санкт-Петербургский государственный университет телекоммуникаций

им. проф. М. А. Бонч-Бруевича»

______________________________________________________________________

Кафедра радиосистем и обработки сигналов

Дисциплина «Математические основы систем автоматического управления»

Отчет по лабораторной работе № 2

«Динамические звенья второго порядка»

Выполнили

студенты гр.

Принял

Ст. пр. каф. РОС

________ Межевов П.А.

Санкт-Петербург

2024

Цель работы: исследование переходных процессов, вызванных ступенчатым воздействием в динамических звеньях второго порядка, определение характера переходных процессов, типа корней характеристического уравнения и устойчивости звеньев.

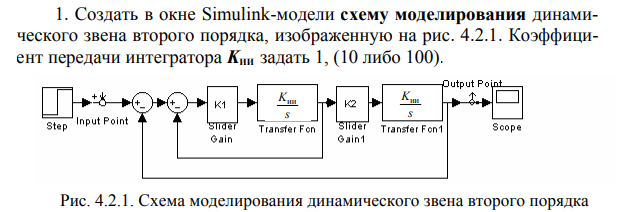
1. Пользуясь правилами структурных преобразований, для данной схемы получить выражения передаточной функции, характеристического уравнения и его коэффициентов d0 , d1 , d2 .

d0=1 d1=1 d2=1

1.2 Используя условия из табл. 4.2.1, рассчитать диапазон изменения коэффициента K2 , в котором переходный процесс является сходящимся апериодическим

Диапазон значений К2 = (0 : 0.33]

1.3-1.4 Проверить результаты расчета K2 на модели и привести график переходного процесса в отчет. Пронаблюдать и зарисовать переходные процессы для двух значений K2 , для которых корни характеристического уравнения являются левыми комплексными

Рис.1 Переходный процесс при К2=0,1

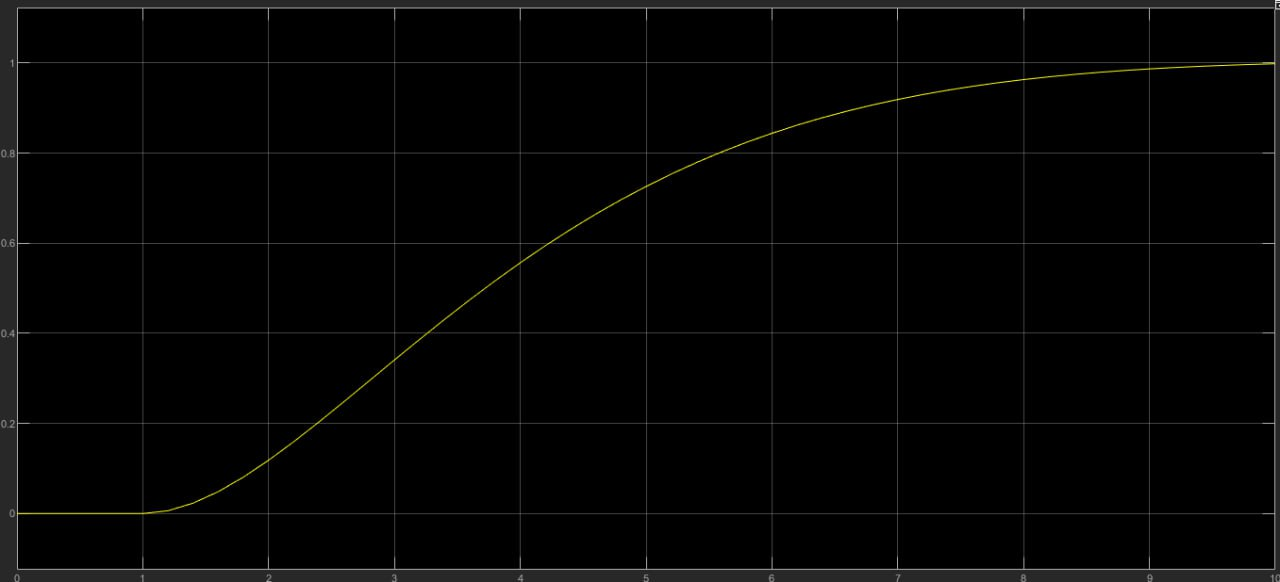
Рис.2 Переходный процесс при К2=0,33

1.5 Для пп. 1.3, 1.4 определить характер переходного процесса, тип звена и его устойчивость.

При К2=0,33 Апериодическое звено устойчивое

При К2=0,1 Интегрирующее звено неустойчивое

2.2 Пользуясь условиями табл. 4.2.1, рассчитать значение коэффициента обратной связи 1 a при котором корни характеристического уравнения звена мнимые 1,2 s j (располагаются на мнимой оси комплексной плоскости), а переходный процесс в звене имеет незатухающий колебательный характер с постоянной амплитудой и частотой.

D0=1 d1=0 d2=0.03 (d2>0) a1=0 a2=0.03

2.3 Проверить результат на модели, зарисовать переходный процесс, получить корни и определить характер переходного процесса, тип звена и его устойчивость.

Рис.3 Переходная характеристика a>0

2.3.2 Убедиться в том, что при значениях a1 , выбранных из диапазона от 0 до 1, переходные процессы являются сходящимися; а выбранных из диапазона от 0 до –1 – расходящимися.

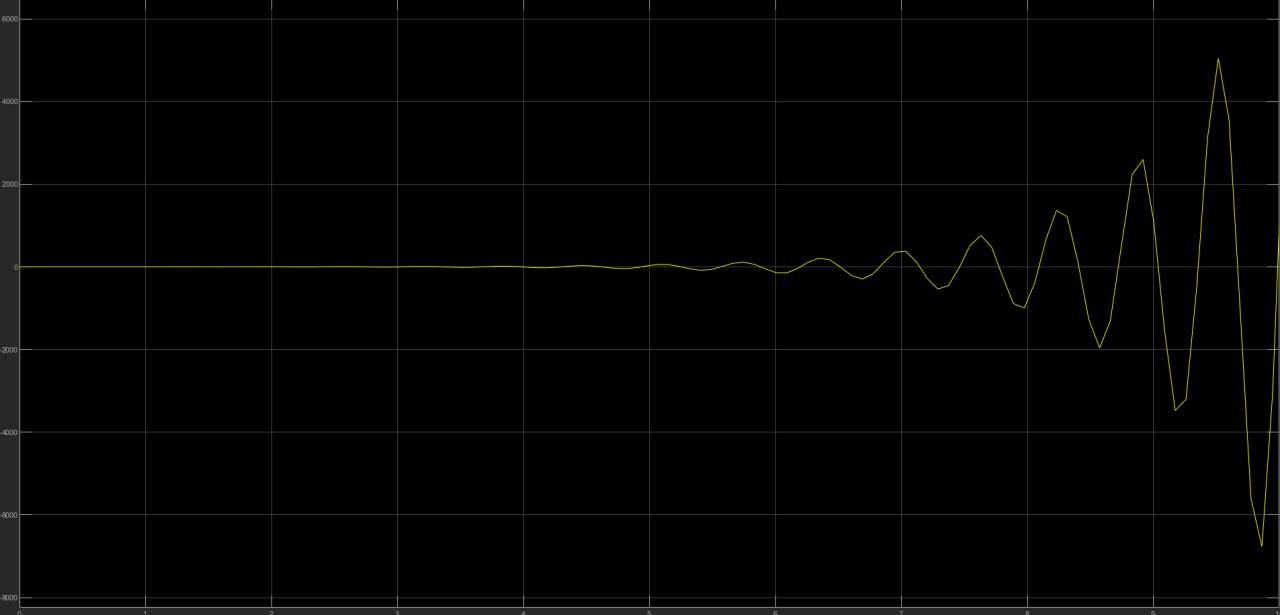
Рис. 4 Переходный процесс при а1<0

2.4 Зарисовать по одному графику переходного процесса для каждого диапазона 1 a , получить корни и определить характер переходного процесса, тип звена и его устойчивость.

При а1<0 колебательное звено, неустойчивое

При а1>0 колебательное звено, устойчивое

2.5. Провести исследование влияния коэффициента обратной связи 2 a на коэффициент передачи звена второго порядка K, изменяя a2 в диапазоне от 0 до 1 .

Рис.5 Переходная характеристика при а2=0

Рис. 6 Переходная характеристика при а2=0.02

Рис. 7 Переходная характеристика при а2=0,5

Рис. 8 Переходная характеристика при а2=1

2.6. Зарисовать графики переходного процесса для двух значений 2 a , определить корни характеристического уравнения и оценить влияние 2 a на корни характеристического уравнения и на коэффициент передачи звена K.

Для а1=0,01 а2=0,02

Рис. 9 Переходная характеристика при а2=0.02

s1=-0.005+0.14*i

s2=-0.005-0.14*i

Для а1=0,01 а2=0,5

Рис. 10 Переходная характеристика при а2=0,5

s1=-0.005 + 0,7*i

s2=-0.005 - 0,7*i

2.7. Используя выражение передаточной функции, доказать влияние a2 на коэффициент передачи звена K.

При изменении а2 коэффициент передачи не изменяется .