
3. ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ИИСТ
отчет
по лабораторной работе №3
по дисциплине «Метрология»
Тема: ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
Студент гр. |
|
|
Преподаватель |
|
Пыко С.М. |
Санкт-Петербург
2022
ЛАБОРАТОРНАЯ РАБОТА № 3
"ЦИФРОВЫЕ ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ"
Цель работы: изучение методов экспериментального определения метрологических характеристик цифровых приборов, а также их применения для измерения физических величин, и оценка погрешностей результатов измерений.
Спецификация средств измерений, применяемых в эксперименте:
Таблица 1 – Спецификация средств измерений.
Наименование средства измерений |
Диапазоны измерений, постоянные СИ |
Характеристики точности СИ, классы точности |
Рабочий диапазон частот |
Параметры входа (выхода) |
Вольтметр универсальный цифровой GDM-8135 |
200Ом - 2000кОм
2МОм
|
0,002Rизм + 1 ед.мл.разр. 0,005Rизм + 1 ед.мл.разр.
|
- |
IR < 1мА IR < 0,1мкА
|
Магазин сопротивлений P33 |
0,1...99999,9 Ом
|
0,2/6*106 |
- |
- |
Обработка результатов измерений
Статическая характеристика преобразования ЦИП.
1. При пределе измерения 20 кОм, шаг квантования равен
q = 20 кОм / 2000 = 0,01 кОм.
Результаты измерений представим в таблице:
Таблица 2 – Измерение статистической характеристики ЦИП
№ изм |
Rп, кОм |
R, кОм |
1 |
0,01 |
0,01149 |
2 |
0,02 |
0,0217 |
3 |
0,03 |
0,03124 |
4 |
0,04 |
0,0406 |
5 |
0,05 |
0,05052 |
6 |
0,05 |
0,0511 |
7 |
0,04 |
0,04143 |
8 |
0,03 |
0,03063 |
9 |
0,02 |
0,02054 |
10 |
0,01 |
0,01006 |
2. Найдём абсолютную основную погрешность прибора на примере 1 измерения в таблице 1 протокола:
ΔR = Rп - R = 0,01 кОм - 0,01149 кОм = -0,00149 кОм
3. Начальный участок графика статической характеристики преобразования прибора согласно показаниям:
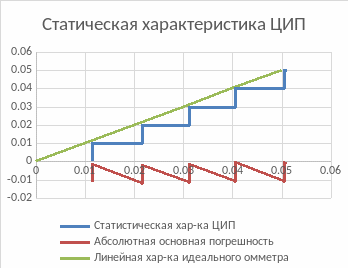
Рисунок 2 - Статическая характеристика ЦИП
Абсолютная инструментальная погрешность.
1. Найдём абсолютную инструментальную погрешность на примере 1 измерения в таблице 2 протокола:
Шаг квантования q = 20 кОм / 2000 = 0,01 кОм
ΔRпN = Rп - 0,5 * q - RN = 2 кОм - 0,005 кОм – 2,006 кОм = -0,011 кОм
2. Результаты измерений и расчетов представим в таблице:
Таблица 3 – Определение абсолютной инструментальной погрешности
№ изм |
RпN, кОм |
RN, кОм |
ΔRиN, кОм |
1 |
2 |
2,006 |
-0,011 |
2 |
4 |
4,01 |
-0,015 |
3 |
6 |
6,011 |
-0,016 |
4 |
8 |
8,07 |
-0,075 |
5 |
10 |
10,018 |
-0,023 |
6 |
12 |
12,023 |
-0,028 |
7 |
14 |
14,025 |
-0,03 |
8 |
16 |
16,031 |
-0,036 |
9 |
18 |
18,03 |
-0,035 |
10 |
20 |
20,039 |
-0,044 |
Определение аддитивной и мультипликативной составляющих погрешности.
1. Построим график абсолютной инструментальной погрешности и тенденции её изменения:

Рисунок 3 - Абсолютная инструментальная погрешность
2. Определим аддитивную и мультипликативную составляющие погрешности по графику (рис. 3):
a = -0,0012
b = -0,0177
Измерение сопротивлений.
1. Найдем погрешности результатов измерений сопротивлений ряда резисторов (по табл. 3 протокола) на примере 1-го измерения:
q1 = Rmax / Nmax = 200 Ом / 2000 = 0,1 Ом
ΔR1 = 0,002Rизм + 1 ед.мл.разр. = 0,002 * 0,1182 кОм + 0,0001 кОм= 0,0003364 ≈ 0,0003 кОм
δ1 = ΔR / Rп * 100% = 0,0003 / 0,1182 * 100% ≈ 0,28%
2. Занесём результаты в таблицу:
Таблица 4 – Измерение сопротивлений
№ |
Диапазон измерения, кОм |
Значение кванта q, Ом |
Rп, кОм |
ΔR, кОм |
δ, % |
Результат измерения, Rп ± ΔR, кОм |
1 |
0,2 |
0,1 |
0,1182 |
0,0003364 |
0,28 |
0,1182 ± 0,0003 |
1 |
2 |
1 |
0,117 |
0,001234 |
1,05 |
0,1170 ± 0,0012 |
1 |
20 |
10 |
0,11 |
0,01022 |
9,29 |
0,11 ± 0,01 |
1 |
200 |
100 |
0,1 |
0,1002 |
100,2 |
0,1 ± 0,1 |
1 |
2000 |
1000 |
- |
- |
- |
- |
1 |
200000 |
10000 |
- |
- |
- |
- |
3 |
0,2 |
0,0001 |
- |
- |
- |
- |
3 |
2 |
0,001 |
- |
- |
- |
- |
Продолжение таблицы 4
№ |
Диапазон измерения, кОм |
Значение кванта q, Ом |
Rп, кОм |
ΔR, кОм |
δ, % |
Результат измерения, Rп ± ΔR, кОм |
3 |
20 |
0,01 |
8,27 |
0,01655 |
0,20 |
8,27 ± 0,02 |
3 |
200 |
0,1 |
8,3 |
0,0167 |
0,20 |
8,30 ± 0,02 |
3 |
2000 |
1 |
8 |
0,017 |
0,21 |
8,00 ± 0,02 |
3 |
200000 |
10 |
- |
- |
- |
- |
Вывод
В данной лабораторной работе были изучены методы экспериментального определения метрологических характеристик цифровых приборов, а также их применения для измерения физических величин.
Исходя их полученных результатов можно сделать вывод о том, что погрешность растет при повышении диапазона измерения, поэтому при измерениях стоит сначала начинать с самых низких диапазонов и закончить таким, который сможет полностью проиллюстрировать значение величины.
