3. Теоретические основы оценки и выбора безопасных кузовных конструкций

Расчетная оценка пассивной безопасности конструкций проводится на основании результатов расчетов их несущей способности по условиям безопасности. В главе 2 были рассмотрены методы, критерии, условия оценки без объяснения содержания теоретических основ и применяемых математических особенностей каждого из методов. Основы теории и алгоритмы расчета являются составной частью рассмотренных в главе 2 методов расчета, применяемых для оценки пассивной безопасности.

3.1. Алгоритм расчета конструкций на пассивную безопасность в

упруго-пластической фазе методом последовательных приближений

Как отмечалось выше, метод базируется на алгоритме упругого анализа работоспособности конструкции в упруго-пластической фазе деформирования. Алгоритм метода включает в себя процедуру итерационного расчета производных силовых схем, получаемых из заданной (исходной) расчетной модели путем последовательного введения свободных шарниров в места возникновения зон пластичности, определяемые упругим расчетом. При этом учитывается переход сечений из упругого состояния в пластическое введением в относительно слабые места модели пластических шарниров. В этом методе реальная характеристика разрушения конструкции при действии аварийной нагрузки аппроксимируется кусочно-линейной, каждый участок которой получается на основе упругого статического расчета. Общая структурная схема метода и алгоритма расчета показана на рис. 3.1. Его основу составляют «упругий» расчет, который выполняется одним из известных методов [3], [50], [28], [4] расчета статически неопределимых систем. В последнее время наибольшее распространение получил метод конечных элементов [8], [12]. Алгоритм расчета методом последовательных приближений включает следующие этапы:

1. «Упругий» расчет заданной (исходной) модели выполняется в условиях действия единичной нагрузки Р, имитирующей характер нагружения в соответствовании с требованиями Правил ЕЭК ООН, ГОСТов, ОСТов или исходя из рассматриваемой аварийной ситуации.

а) определение внутренних усилий M_i в узлах, перемещений Z_i и деформации S_р модели (перемещения точки приложения нагрузки) в направлении действия единичной силы. Для стержневого элемента под M_i подразумеваются: нормальные усилия N, изгибающие моменты и , крутящий момент , поперечные силы V, W и , бимомент В, учитывающий стесненное кручение. Их выражения имеют следующий вид:

= – M_x –  (y_A – y_C); = – M_y –  (x_A – x_C);

= – M_к + V (x_A – x_E) – W (y_A – y_E), (3.1)

где x_A, x_C, y_A, y_C, x_E, y_E – координаты точек приложения поперечных усилий и центров изгиба;

б) определение максимальных напряжений в стержневых элементах и предельной по текучести нагрузки Р_т по наибольшим значениям из них с учетом косого изгиба из следующих выражений:

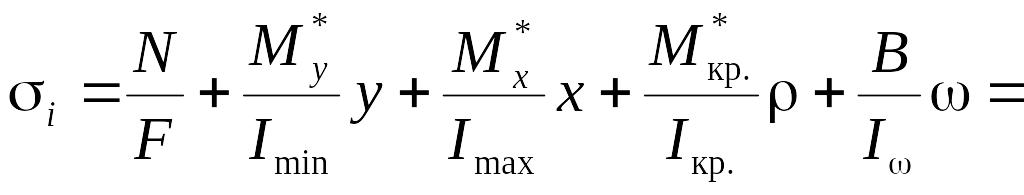
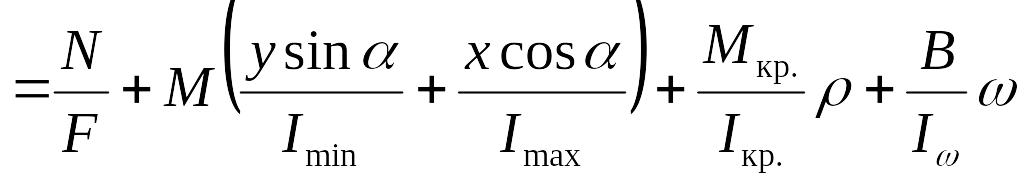, (3.2)

где I_min и I_max , I_кр, I_ – осевые, полярный и секториальный моменты инерции сечения;  – угол между главной осью сечения и плоскостью действия изгибающего момента;

. (3.3)

2. Определение условных пластических напряжений _1i в исходной схеме от единичной нагрузки

_1i = M_1i cos  / W_плi , (3.4)

где М_1i – изгибающий момент в i-ом элементе (узле) исходной схемы;  – угол между нейтральной осью сечения и плоскостью действия изгибающего момента; W_плi – пластический момент сопротивления в i-м сечении.

3. Нахождение предельной пластической нагрузки Р_плI , соответствующей появлению первого пластического шарнира

Р_плI = min Р_плi = _т / _1i = _т W_плi / М_1i cos  . (3.5)

3. Определение условных пластических напряжений _пл.I от Р_пл.I и запаса несущей способности _нс из следующих выражений:

_плI = _1i  _плI ; _нс = _т – _плI . (3.6)

3. Расчет производной схемы с одним свободным шарниром, имеющей степень статической неопределимости (n – 1), и определение характеристик, указанных в п. 1а.

4. Определение _2i по формуле (3.4) при подстановке в нее М_2i вместо М_1i , где М_2i – момент в i-м элементе производной схемы.

5. Нахождение Р_пл.II , соответствующей появлению второго пластического шарнира

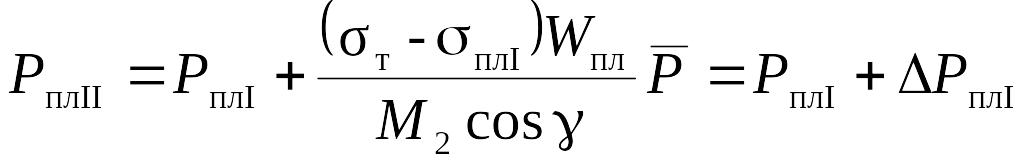. (3.7)

Второе слагаемое соответствует наименьшему значению приращения нагрузки Р_плI . Второй пластический шарнир появляется там, где возникают относительно наибольшие значения напряжений.

3. Определение условных пластических напряжений от силы Р_плII

_плII = _плI + _плI ; _плI = _2i  P_плI . (3.8)

3. Расчет схемы с двумя свободными шарнирами, имеющей степень неопределенности (n – 2), и далее итерационный расчет производных схем до превращения исходной схемы в пластический (кинематический) механизм с числом пластических шарниров, равным (n + 1).

4. Определение разрушающей нагрузки Р_р , энергоемкости Е_к , деформаций S модели по направлению действия Р_р, остаточного пространства L_ост . Первые два критерия определяются из выражения:

. (3.9)

Допускаемая деформация S_доп определяется по формуле (2.10). Деформация S_N соответствует моменту превращения модели в кинематический механизм и находится, как

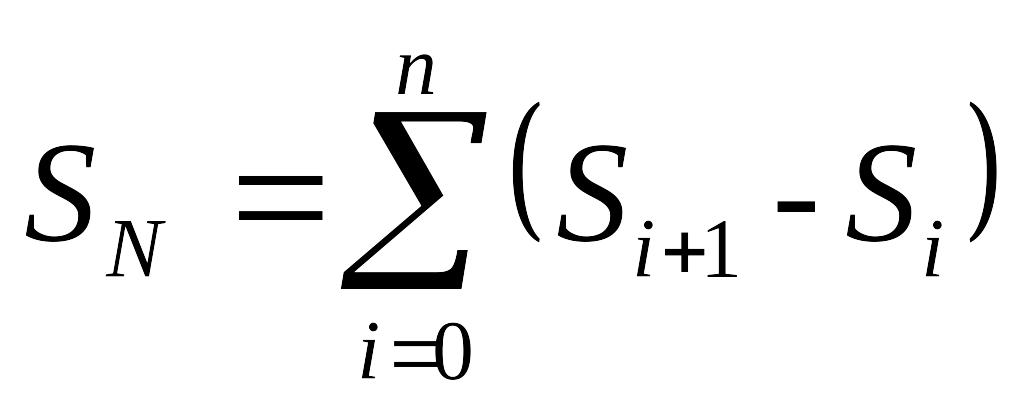. (3.10)

3. Оценка безопасности конструкции по первым пяти критериям условия (2.2).

Приведенные формулы и выражения соответствуют расчету стержневой модели. При выводе формул (3.4)...(3.8) приняты следующие допущения:

• учтено действие только изгибающих моментов;

• принята идеальная упруго-пластическая диаграмма Прандтля;

• сечения элементов считаются недеформируемыми в своей плоскости, а сами элементы не теряют устойчивость до момента разрушения конструкции.

Более подробно условия поведения конструкций и их сечений при пластическом разрушении рассмотрены ниже в подразд. 3.2.1.

3.2. Выбор безопасных силовых схем кабин и кузовов на основе

расчета их конструкций по предельному состоянию

Расчет статически неопределимых конструкций кузовов и кабин с учетом пластических деформаций элементов особое значение приобретает при оценке их работоспособности в условиях действия аварийных нагрузок.

Рассматриваемый инженерный метод расчета кузовных конструкций на безопасность [25], [30], [31], [33], [34] основан на применении кинематической теоремы теории предельного равновесия [23], [64]. При этом конструкция рассматривается в момент ее разрушения, превращения в пластический (кинематический) механизм, когда в ней образуется количество пластических зон (шарниров), в общем случае на единицу превышающее степень статической неопределимости. Пластический механизм (механизм разрушения) характеризуется известными внутреннеми усилиями М_плi в пластических шарнирах, возможностью его движения при постоянном неизменном значении разрушающей нагрузки Р_р . В момент возникновения пластического механизма система находится в состоянии равновесия. При этом внутренние усилия в системе не превосходят предельных значений и удовлетворяют условиям пластичности. Основным физическим свойством, используемым при расчетах по предельному состоянию, является пластичность металла, из которого состоят кузовные конструкции.

3.2.1. Основы теории. Методика расчета конструкций на безопасность

Несущая способность кузовов и кабин при действии аварийных нагрузок, в основном, определяется способностью силовых элементов в местах их соединения воспринимать пластические изгибающие моменты М_плi и оказывать сопротивление изгибу элементов, а в отдельных случаях и кручению. Основные узлы соединения силовых элементов конструкции, как правило, являются перегруженными и именно в них появляются при разрушении зоны пластичности. В расчетах влиянием распространения пластических зон вдоль элементов можно пренебречь. Теоретически считается, что эта зона сконцентрирована в концевом сечении элемента около узла. Это место называют пластическим шарниром. В нем текучесть охватывает все сечение. Пластический шарнир возникает при определенном пластическом моменте М_плi. В реальных условиях этому моменту соответствует большая кривизна элемента на малой длине элемента.

Основные допущения инженерного расчета:

1. Принимается диаграмма жестко-пластического течения (упрощенная диаграмма Прандтля) в пластическом шарнире и разрушения конструкции под действием разрушающей нагрузки.

2. Пренебрегается влиянием продольных сил и скручивающих моментов на образование пластических шарниров.

3. Пренебрегается работой внутренних усилий на упругих деформациях элементов.

4. Принимается статическая аппроксимация процесса аварийного нагружения.

5. Не учитывается потеря формы (депланация) сечения в пластическом шарнире.

Подобная идеализация не всегда соответствует реальной картине разрушения конструкции. Однако она существенно упрощает расчет и дает результаты весьма близкие к экспериментальным, особенно для каркасных конструкций кузовов [26], [66]. В общем виде задача предельного равновесия в упруго-идеальнопластической формулировке представляется функцией Лагранжа

L (p, Q, U, ) = р + U^T (H^TQ - рr) - ^T(Q) , (3.11)

где Q – обобщенные внутренние усилия;  – вектор положительных множителей Лагранжа (  0); Ф(Q) – вектор-функция потенциалов пластичности; U – матрица перемещений; Н – матрица кинематических связей; р – вектор проекции внешних сил на координатные оси.

Решение задачи позволяет выделить условия текучести и упругости

(Q) = 0 ; (Q) < 0 . (3.12)

При рассмотрении жестко-пластического течения процесса второе условие упругости не учитывается. Поэтому функция (3.11) приобретает вид

L = р + U^T (H^TQ - рr) . (3.13)

Для состояния предельного равновесия в кинематической формулировке рассеиваемая внутренними усилиями мощность должна быть минимальной на основании теоремы Куна-Таккера о седловой точке функционала Лагранжа. При этом кинематическая теорема теории предельного равновесия гласит, что для всех значений нагрузок Р, образующих кинематический пластический механизм, существует нижнее предельное значение Р_действ = min P_pi . Тогда основное уравнение метода – равенство работ внешних А и внутренних U усилий имеет вид

L

L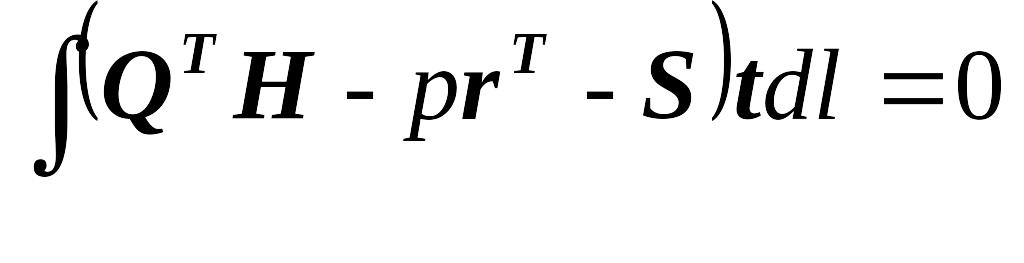

(3.14)

Уравнение записано с учетом того, что

L

L

L

L

L

L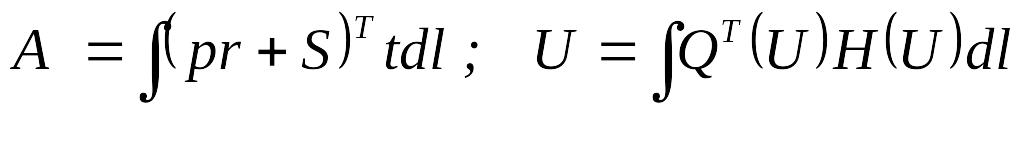

, (3.15)

где S – вектор проекции внешней нагрузки; t – вектор, касательный к траектории L; dL – положительная мера (дифференциал) длины траектории L; А_L и U_L – работы внешних и внутренних усилий.

При деформировании конструкции совершается конечная работа на конечных деформациях. Число внутренних деформаций конечно и равно Ш. Число внешних нагрузок также конечно и равно K. Вариации работ внешних и внутренних усилий на малых деформациях представляют собой линейные функции последних. Поэтому основное уравнение инженерного метода расчета конструкций по предельному состоянию можно записать в виде равенства работ внешних сил и внутренних усилий на возможных вариациях перемещений

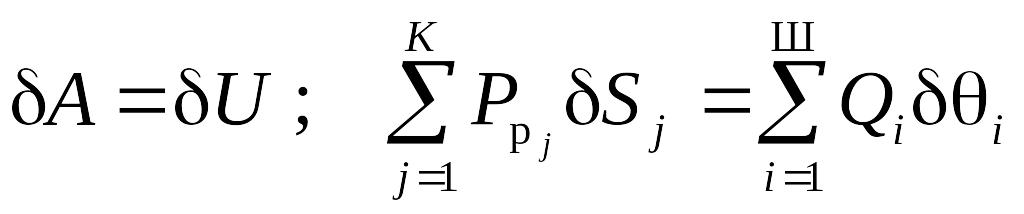, (3.16)

где S_j – деформация конструкции по направлению действия j-той внешней разрушающей силы ; _i – угол относительного поворота силовых элементов в i-том пластическом шарнире.

В общем случае под обобщенными внутренними усилиями Q_i , возникающими в пластических зонах (шарнирах), подразумевается действие пластических изгибающих и крутящих моментов, нормальных сил, вызывающих появление этих шарниров. При рассмотрении жестко-пластического характера разрушения конструкции, как уже отмечалось, влиянием упругих деформаций можно пренебречь. В расчетах кузовных конструкций на безопасность это допустимо, так как при их разрушении упругая составляющая деформаций не превышает 10% от общих значений [31], [32]. Поэтому в случае учета действия в пластических шарнирах только изгибающих моментов при воздействии одной аварийной нагрузки, уравнение (3.16) запишется в виде

, (3.17)

где n – степень статической неопределимости конструкции.

Предельный пластический момент М_пл вычисляется по формулам

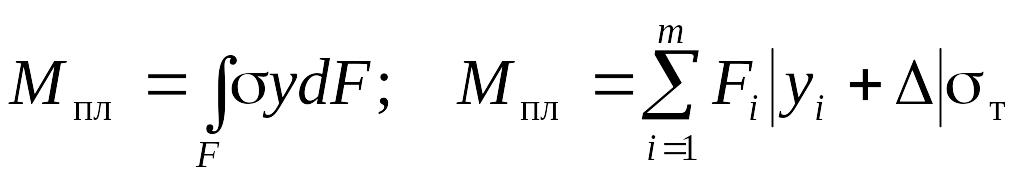, (3.18)

где F_i – элементарная площадка (стенка) тонкостенного сечения; y_i – расстояние от центра тяжести i-той площадки до нейтральной оси сечения;  – смещение линии равных площадей сечения относительно нейтральной оси.

Во второй формуле (3.18) первый сомножитель представляет собой пластический момент сопротивления W_плi сечения:

. (3.19)

Методика инженерного расчета конструкции на безопасность. При заранее известном пластическом механизме разрушения [24], [31] она включает следующие этапы: