
- •Метод распараллеливания по данным
- •Основывается на распределении данных по процессорам:
- •Условия применения метода
- •Основные задачи, которые надо решать при распараллеливании по данным
- •Метод распараллеливания по данным – некоторая формализация в простом случае
- •В задаче 1) - распределении данных необходимо
- •В этих предположениях, вид формул, используемых в методе распараллеливания по данным.
- •Задача 2) - распределение вычислений при известном распределении данных решается автоматически
- •Теневые грани – области памяти, необходимые для хранения удаленных данных в процессоре, в
- •Правило собственных вычислений: вычисляемые данные вычисляются в процессоре, в котором они распределены.
- •Задача 3) определение удаленных данных – решается в результате анализа информационных зависимостей между
- •Задача 4) - определение операторов обмена удаленными данными и места их расположения в
- •Задача 5): правила написания текста параллельной программы
- •C Фрагмент 1 параллельной программы – первый цикл
- •C Фрагмент 2 параллельной программы – второй цикл
- •C Фрагмент 3 параллельной программы – третий цикл и прием удаленных
- •C Фрагмент 4 параллельной программы – отправка удаленных
- •С Итоговая программа
- •C Второй цикл
- •Замечания к программе

Метод распараллеливания по данным

Основывается на распределении данных по процессорам:
Массив A
Процессоры |
P1 |
P2 |
P3 |
|
|||
|
Память |
Память |
Память |
Процессоры |
P1 |
P2 |
P3 |
|
|||
|
Часть |
Часть |
Часть |
|
массива |
массива |
массива |
|
А |
А |
А |

Условия применения метода
1.Наличие локальной памяти у процессоров – метод ориентирован на многопроцессорные системы с распределенной памятью
2.Распределение (разделение) многомерных массивов. Фактически – распределение (разделение) сетки, покрывающей пространство решаемой задачи. Предположение о примерно одинаковом времени счета в каждой точке пространства

Основные задачи, которые надо решать при распараллеливании по данным
1)распределение данных;
2)распределение вычислений;
3)определение удаленных данных;
4)определение операторов обмена удаленными данными и места их
расположения в программе;
5) правила написания текста параллельной программы (описания переменных, циклы, маски операторов); модификация текста последовательной программы в случае распараллеливания

Метод распараллеливания по данным – некоторая формализация в простом случае
Распределенная размерность массива X – размерность, по которой проводится распределение (разделение) данных.
В задаче 1) - распределении данных необходимо
для каждого массива X(n1 : m1 , … nk : mk) определить распределенные размерности.
а) массивов много – как это делать согласованно б) сколько размерностей в) какие размерности
В рассматриваемом простом случае будем считать, что эта задача решена
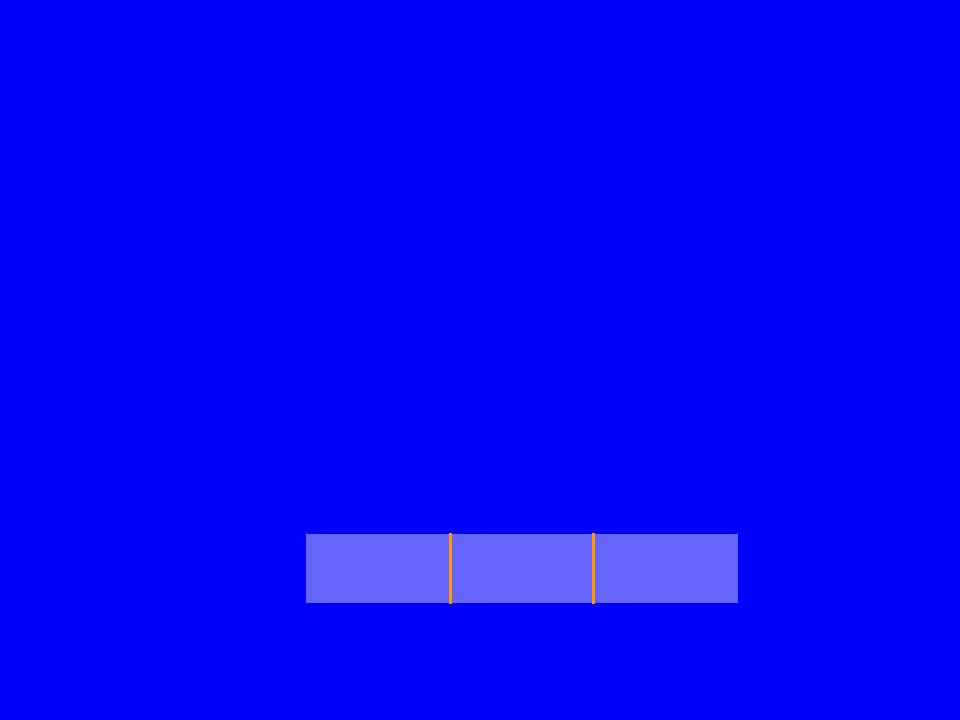
В задаче 1) - распределении данных необходимо
для каждой распределенной размерности r, X(… , nr : mr, …), определить функцию F, задающую для каждого значения индекса i,
nr <= i <= mr, номер процессора iproc, которому это значение принадлежит, то есть
iproc = F(X, r, i)
В рассматриваемом простом случае будем считать, что эта задача решена – используется блочное распределение (распределение одинаковыми подряд расположенными фрагментами).
Массив
A(1:L)

В этих предположениях, вид формул, используемых в методе распараллеливания по данным.
iproc - число процессоров (задается при нумерации от 1 до k,
в MPI нумерация от 0 до k-1 ).
Глобальный и локальный индексы.
1.Число точек ipoints в одном процессоре после равномерного блочного распределения n точек распределенной размерности на iproc процессоров.
ipoints=(n-1) / iproc +1, где n = mr – nr + 1
2.Номер процессора nproc, в котором находится точка с глобальным индексом iglobal:
nproc = iglobal / ipoints +1
3.Значение индекса iglobal, меняющегося от 1 до n, через соответствующее значение локального индекса ilocal в процессоре с номером myrank:
iglobal = ilocal + (myrank-1) * ipoints
4.Значение индекса ilocal через iglobal
ilocal = iglobal - (myrank-1) * ipoints

iglobal = 1, … ,L
Массив
A(1:L)
Процессоры |
P1 |
P2 |
P3 |
|
|||
|
Часть |
Часть |
Часть |
|
массива |
массива |
массива |
|
А |
А |
А |
ilocal = 1,…,ipoints ilocal = 1, … ,ipoints |
ilocal = 1, … ,L-2*ipoints |
||
Например, необходимо для вычислений вида :
последовательная программа |
параллельная программа |
|
do i = 1,n |
|
do i = in, ik |
x(i) = i +3*y(i) |
|
x(i) = iglobal +3*y(i) |
enddo |
|
|
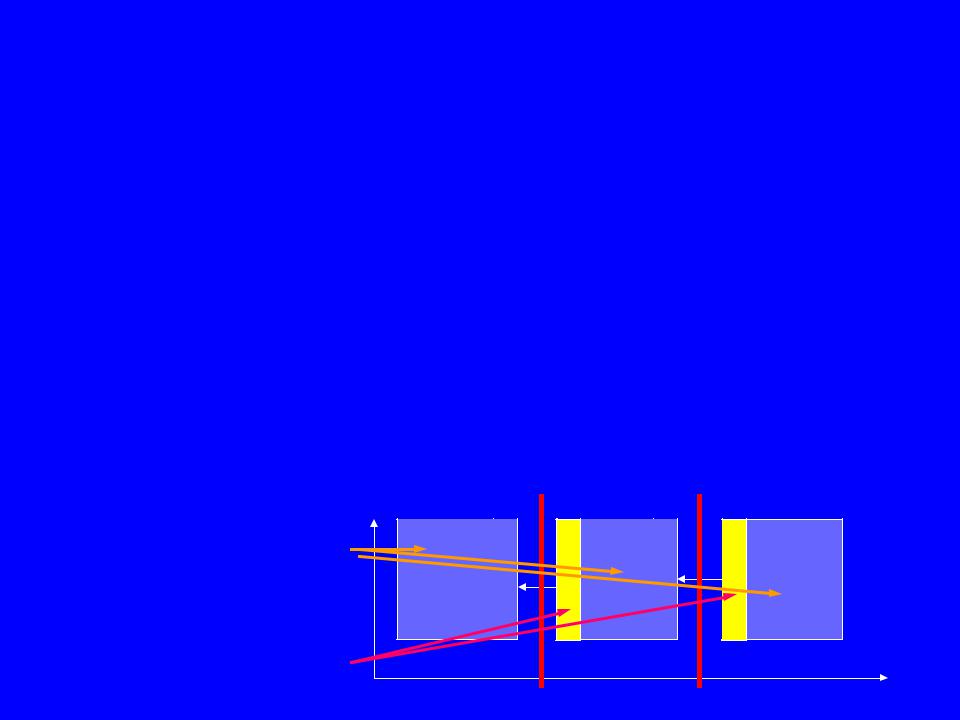
Задача 2) - распределение вычислений при известном распределении данных решается автоматически
Вычисляемые данные – переменные, в которые проводится запись значений (например, переменные с индексами в левых частях операторов присваиваний).
DO i=1,95
X(i)=1 ! X (i), i=1,95 – вычисляемые данные ENDDO
Требуемые данные – переменные, которые требуются для вычисления значений (например, переменные с индексами в правых частях операторов присваиваний или в условиях операторов IF ).
DO i=1,20
X(i) = Z(i+2) ! Z (i), i=3,22 – требуемые данные ENDDO
Требуемые данные могут быть собственными – находиться после распределения в том же процессоре, что и вычисляемые данные, для которых они требуются, либо удаленными – находиться в других процессорах.
Собственные элементы Z |
Z |
Z |
Z |
|
|
|
|
ipoints =10, iproc =3 |
|
|
|
Удаленные элементы Z |
P1 |
P2 |
P3 |
|
|
|
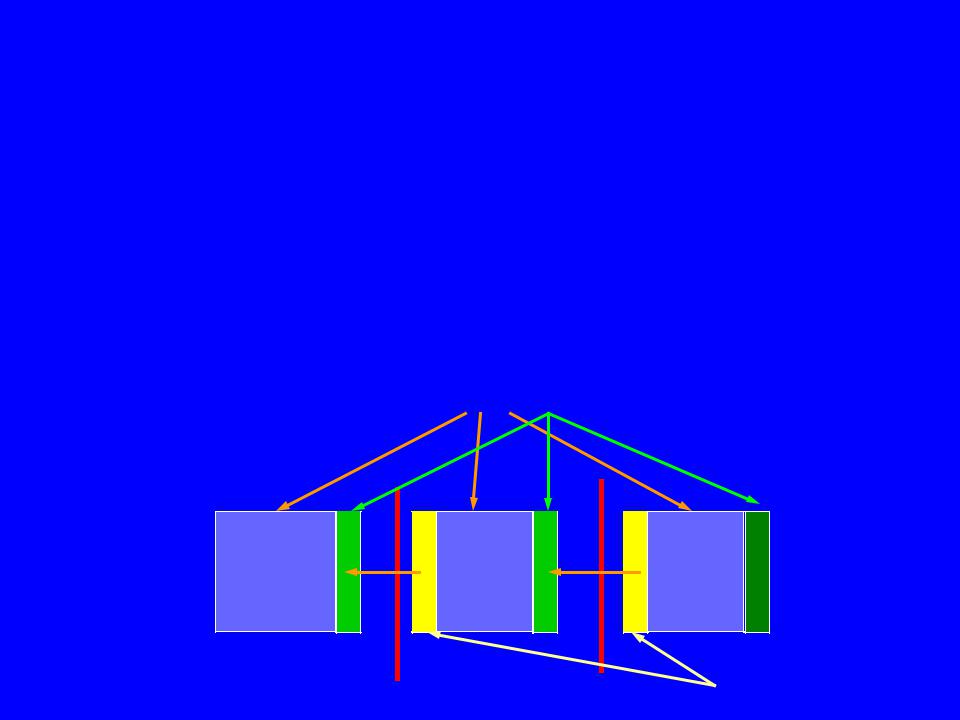
Теневые грани – области памяти, необходимые для хранения удаленных данных в процессоре, в котором они требуются.
Пример.
DO i=1,20
X(i) = Z(i+2) ! Z (i), i=3,22 – требуемые данные ENDDO
Описание распределенного массива Z
DIMENSION Z(1:ipoints + 2 )
Z |
ipoints =10, iproc =3
Z |
Z |
Удаленные данные Z(1:2)
