2 семестр Лекции Гришин / F-02-Lektsia_9

n

b

ТогдаVG lim VG

lim

S( k ) tk

S(x)dx .

0

0

k 1

a

Пример 1

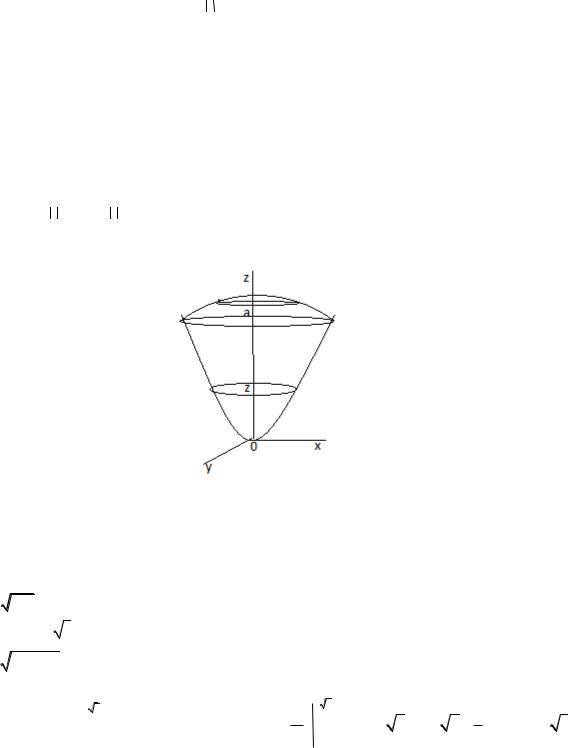
Найти объем общей части параболоида 2az x2 y2

и сферы x2 y2 z2 3a2 .

z a .

y

2az

z 0

x

2

2

2 z

2

2az 3a

2

0

2

y

2

3a

2

z

a

x

z

Для

t

0; a

площадь сечения тела плоскостью z t

равна площади круга радиуса

r

2at

, т.е. S(t) 2 at

a; a

t

Для t

3

сечение тела плоскостью z

представляет собой круг радиуса

r

3a2

t 2 , поэтому функция площади сечения на этом отрезке равна S(t) (3a2

t2 ) .

Тогда объем тела

a

a

3

t

3

a 3

1

a

3

6

3 5

V a

2tdt

(3a

2

t

2

)dt a

3

2

t

a

3

3a

3

3 3 3 3

3

3

0

a

t a

ФОРМУЛА объема тела вращения.

Если криволинейная трапеция, ограниченная осью ОХ, прямыми x a

и x b , графиком

функции f (x) 0

, вращается вокруг оси ОХ, то в пространстве образуется тело Grot ,

называемое телом вращения. Сечения тела

Grot плоскостями, перпендикулярными оси ОХ,

представляются кругами радиуса r f (x) . Поэтому S(x) f 2 (x) и

b

V

f 2

(x)dx .

rot

РЕШЕНИЕ. Криволинейная трапеция ограничена окружностью x

2

y

2

R

2

на

R

x

3

R

4 R

3

отрезке R; R , VR

R

dx

2

2

2

x

R

x

3

3

R

R

0; 2a

, y(t), t

0;

Сечение тела вращения плоскостью y

представляет собой

кольцо с внутренним радиусом r xA x(t) и внешним радиусом R xB 2 a x(t) .

Площадь сечения при фиксированном y равна S ( y) R

2

r

2

и объем тела вращения

2a

V

S ( y)dy (2 a x(t))2 x2 (t) y (t)dt 4 2a2 4 ax(t) y (t)dt

0

0

0

причем max Ak 1 Ak . Боковая поверхность пирамиды

Kn равна

k

1

n

1

1 n

S

Kn

h

A

A

L P

(h L) A A

, где P

- периметр вписанного

k

k 1

k

2

n

k

k 1 k

n

2 k 1

2 k 1

многоугольника, hk - высоты боковых граней.

Площадью боковой поверхности конуса называют число, равное Sбок

lim SK .

n

n

При n и 0 ,

Pn 2 R , hk L 0 , поэтому lim SKn

RL .

n

с образующей L1

r

rL

. Тогда Sбок. усеч. R(L1 L) rL1 RL (R r)L1

sin

R r

RL

(R r)rL

(R r)L .

R r

x x(t),

, t ; с непрерывно

Пусть кривая на плоскости задана через параметр

y y(t)

0

дифференцируемыми функциями x(t), y(t) . Каждому разбиению

t0 ,t1,...,tn ,tn 1

отрезка ; соответствует ломанная, вписанная в дугу

кривой, с отрезками, соединяющими точки Ak x(tk ); y(tk ) , k 1,2,...,n

n

2

2

n

2

2

S ,rot y(tk 1 ) y(tk )

xk

yk

2 y( k )

xk

yk

,

k 1

k 1

где xk x(tk ) x(tk 1 ) , yk y(tk ) y(tk 1 ) ,

2 y(

k

) y(t

k 1

) y(t

k

),

k

t

k 1

;t

k .

ОПР. Площадью поверхности вращения называют предел S

lim S

, если он

rot

0

,rot

По теореме о среднем Лагранжа существует набор

и

1, 2

,..., n

1 ,

2 ,..., n

и yk

точек на отрезках tk 1 ;tk , для которых xk x ( k ) tk

y ( k ) tk .

n

x (t) 2

y (t 2 непрерывна в

Тогда S ,rot 2 y( k ) x ( k ) 2 y ( k 2 tk

. Функция

k 1

каждой точке k отрезка ; , поэтому x ( k ) 2 y ( k 2

x ( k ) 2

y ( k 2

o(1) ,

где o(1) - бесконечно малая при 0 . Тогда

n

Первое слагаемое 2 y( k )

2

2

xk является интегральной суммой

(x ( k ))

( y ( k ))

k 1

2

2

на отрезке ; и она, согласно предположениям, имеет

функции 2 y(t) x (t)

y (t)

предел, равный интегралу, при

0

. Тогда тот же предел имеет площадь поверхности

конического тела.

Пример 4. Найти площадь поверхности вращения астроиды x a cos

3

t, y a sin

3

t вокруг

a

x

a

2x

a2

2x x a

a2

S 2 a ch2

dx a (1 ch

)dx a2

sh

2 sh2

a

a

2

a

x 0

2

0

0

Если кривая задана в полярной системе координат уравнением

r r( ), ;

, то его

x r( ) cos

x r cos r sin

x 2 y 2

r 2 r 2 .

можно перевести в параметр

y r( )sin

y r sin r cos

r

2

2a

2

cos 2 0

0;

4

2a

4

sin

2

2

4a

4

sin

2

2

4a

4

cos

2

2

4a

4

2r r 4a

2

sin 2 r

2

r

2

r

2

r

2

r

2

r

2

/ 4

1

0

/ 4

S / 2 4 a2

r sin

r

d 4 a2 cos

4 a2

1

2 / 2

S 4 a2

(2

2)

0