
2 семестр Лекции Гришин / F-02-Lektsia_8
.pdf
Ф-02-Лекция 8. |
Приложения определенного интеграла. Площадь, длина кривой. |
||||||||||||||||||||||||||
1. Площадь криволинейной трапеции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Аксиоматика площади. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Площадью называют функцию S(G) 0 , определенную на областях G |
плоскости |
||||||||||||||||||||||||||
называемых измеримыми, удовлетворяющую условиям: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
1) Площадь квадрата со стороной1 равна 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2) Площадь прямоугольника со сторонами a и b равна a b . |
|
|
|
|
|
|
|
||||||||||||||||||||
3) Если область G G1 |
G2 , где G1 и G2 измеримы и пересекаются только по границе, то |
||||||||||||||||||||||||||
G измерима и |
S |
|
G G |
|
S (G ) S (G ) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
2 |
1 |
2 |
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
2 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||
4) Если фигуры G |
и G измеримы и G |
G , то S |
G |
|
S |
G |
|
. |
|
|
|
|
|
||||||||||||||
Область Gin , являющаяся объединением конечного числа прямоугольников, |
|||||||||||||||||||||||||||
пересекающихся только по границе так, что Gin |
G |
, называется объемлемой областью G . |
|||||||||||||||||||||||||
Область Gon , являющаяся объединением конечного числа прямоугольников, |
|||||||||||||||||||||||||||
пересекающихся только по границе так, что G Gon |
, называется объемлющей для G . |
||||||||||||||||||||||||||
Верхней мерой области G |
|
||||||||||||||||||||||||||
, обозначение |
S |
G inf S (Gon ) , нижней мерой области G , |
|||||||||||||||||||||||||
обозначение |
S |
|
G |
|
sup S |
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
in |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Всякая ограниченная область G на плоскости имеет нижнюю меру |
S |
|
G |
и всякая область |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
G , имеющая внутреннюю точку, имеет верхнюю меру |
S |
|
G |
. |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
Область G измерима, если |
S |
|
G |
|
S |
|
|
|
|||
Точка M внутренняя для области G |
|||||
некоторым кругомU (M ) |
радиуса |
||||
,
G |
|
S |
|
G |
. |
|
|
|
если она принадлежит этой области вместе с с центром в точке M .
Точка N называется граничной для G , если 0в кругеU (N) есть внутренние точки
для G , а также точки не принадлежащие G . Объединение граничных точек называется границей области G , обозначение G .
Теорема. Для измеримости области G необходимо и достаточно, чтобы мера ее границы
была равна нулю. |
|
|
|
|
||
Док. |
|
|
|
|
|
|
G |
, G G G |
G |
0 ( G) G |
(G ) |
|
|
on |
in |
on |
in |
on |
in |
|
|
|
|
|
|
n |
n |
Если область G измеримая, то существует последовательность областей Gon |
и Gin , по |
|||||
которой lim |
n |
|
n |
. Тогда по лемме о полицейских, |
||
(Gon ) (Gin ) (G) (G) 0 |
||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
( G) 0 ( G) 0 |
|
|
|
|||
Обратно, пусть мера границы нулевая, а (G) не существует, т.е. (G) (G) |
||||||
|
|
|
|
|
|
|
Тогда 0 Gon ,Gin : (Gon ) (Gin ) , для которых (G) (G) (Gon ) (Gin )
Последнее бывает только при (G) (G) 0
Криволинейной трапецией называют фигуру на плоскости, ограниченную осью ОХ, прямыми с уравнениями x a и x b , кривой графика функции f (x) 0 , определенной на
отрезке a;b .
Пусть x0 , x1,..., xn разбиение отрезка a;b . В качестве объемлющей фигуры Gon ( ) для криволинейной трапеции выбираем также криволинейную трапецию, построенной для

кусочно-постоянной функции
|
k |
|
f (x) |
||
|
||
|
|
max |
|
f (x), x x |
k 1 |
; x |
k |
||
x x |
k 1 |
;x |
|
|
|
||
|
k |
|
|
|
|
|
|
|
|
k |
1,2,...,n |
|
|
|
|
,
. Аналогично,
объемлемой фигурой Gin ( ) для криволинейной трапеции будем считать криволинейную
трапецию, построенную для кусочно-постоянной функции |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
k |
|
min |
|
f (x), x x |
k 1 |
; x |
k |
, |
n |
|
|
n |
|||
|
|
|
|
|
|
|
|
|
x xk 1 ;xk |
|
|
|
. Тогда S Gon |
( ) k xk |
и S Gin ( ) k xk . |
||||||
f |
|
(x) |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
k 1,2,...,n |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
k 1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
S |
|
G |
( ) |
и |
S |
|
G ( ) |
|
являются интегральными суммами (верхняя и нижняя интегральные |
||||||||||||
|
|
on |
|
|
|
in |
|||||||||||||||
суммы Дарбу). Если разбиение , то сумма S Gon ( ) убывает, |
|
|
|||||||||||||||||||
а |
S |
G |
|
( ) |
|
|
- возрастает. |
|
|
|
|
|
|
|
|
||||||
|
|
in |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
Если функция f (x) |
интегрируема, то inf S Gon ( ) sup S Gin ( ) |
|
|
f (x)dx . |
|||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
Последнее является геометрическим смыслом интеграла Римана.
Если
f (x) 0
на отрезке
a;b
, то площадь криволинейной трапеции равна
S
- b f (x)dx .
|
|
a |
Если функция меняет знак на отрезке a;b , то на отрезках, где f (x) 0 интеграл |
||
со знаком +, а на отрезках, где f (x) 0 |
, интеграл берется со знаком минус. |
|
Элементарной областью |
Фx на плоскости называют фигуру, ограниченную |
|
прямыми с уравнениями |
x a и x b |
, графиками непрерывных функций y f ( |
y g(x) f (x) g(x), x a;b . |
|
|
берется
x) и
Элементарной областью Фy прямыми с уравнениями y c x ( y) , ( y) ( y), y c;d
на плоскости называют фигуру, ограниченную
и y d , графиками непрерывных функций x (
y) и
ФОРМУЛЫ вычисления площади элементарной фигур Фx иФy .
|
b |
d |
|
Sx |
( f (x) g(x))dx |
и S y ( ( y) ( y))dy . |
|
|
a |
c |
|
ДОК. Если Ф f |
и Фg - криволинейные трапеции, соответствующие функциям y |
||
y g(x) на отрезке a;b и f (x) g(x) 0, x a;b , то Ф f Фg |
Фx . |
||
f (x)
и
|
|
|
|
|
|
b |
b |
b |
Тогда SФ f |
SФg |
Sx |
S x |
SФ f |
SФg |
f (x)dx g(x)dx f (x) g(x) dx . |
||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
a |
a |
a |
Если f (x) g(x), x a;b , но g(x) 0 на некоторых промежутках, то существует число A 0 , для которого для функций f (x) f (x) A и g (x) g(x) A выполняется условие f (x) g (x) 0, x a;b . Площади элементарных фигур, построенных для функций
f (x), g(x) и f (x), g (x) на отрезке a;b равны, т.е.
S |
x |
|
S x
b f (x)
a
A g(x)
A dx
b f
a
(x)
g(x) dx
.
Формула для площади фигуры Фy |
доказывается аналогично. Площадь имеют фигуры, |
|
являющиеся конечным объединением элементарных областей типаФx |
и Фy . |
|
Пример 1 |
|
|
|
|
|
|
|
|
||
Найти площадь области, ограниченной осями координат и кривой x |
y a |
||||||
y |
a |
x 0 x 0; a |
|
|
|
||
Замена. t |
x |
|
0; |
a |
|
x t |
2 |
, dx 2tdt, |
y |
a t |
|
|
|||||||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
Вычисление площади криволинейной трапеции:
y a t 2
2t |
a |
.
a |
|
|
t |
4 |
|
2t |
3 |
|
|
t |
2 |
|
t |
a |
|
a |
2 |
|
2a |
2 |
|
a |
2 |
|
a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
S 2 t t |
|
2t |
|
|
|
a a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
a a dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
4 |
|
3 |
|
|
2 |
t 0 |
|
|
3 |
|
3 |
|
|
2 |
|
6 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
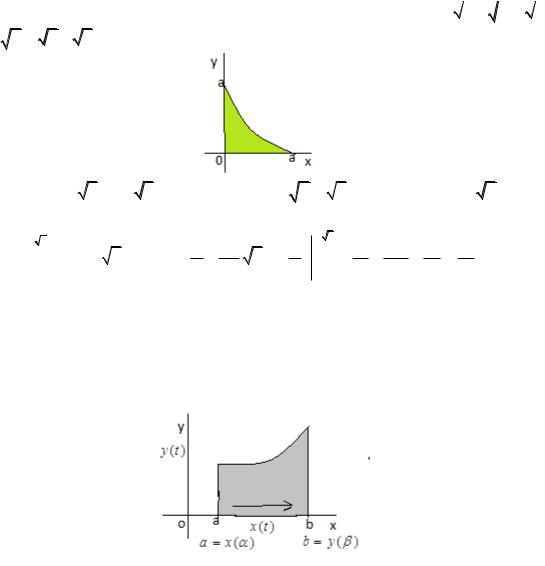
Если граница криволинейной трапеции задается через параметр |
x x(t) |
||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y y(t), |
||
x(t) возрастающая функция, |
|
y(t) 0 |
, |
x( ) a , |
x( ) b . Тогда |
|
|
|
|||||||||||||||||||
t
;
.
S
Действительно, по доказанному Sx
|
|
|
|
|
Если x (t) 0 |
, то Sx |
|
|
y(t)x (t)dt |
|
||||
|
|
|
|
|
x
y(t)x (t)
b y(x)dx
a
dt .
y(x(t))x (t)dt
y(t)x (t)dt
.
Площадь области ограниченной замкнутой кривой, заданной через параметр (направление обхода против часовой стрелки)

Площадь выделенной части
sk ,m
t |
k |
1 |
t |
m 1 |
|
|
|
|
|
||||
y(t)x (t)dt |
y(t)x (t)dt S sk ,m |
|||||
|
t |
k |
|
t |
m |
m,k |
|
|
|
||||
|
|
|
|
|
||
y(t)x (t)dt
.
Если область представляется как стандартная область по y , то ее площадь вычисляется по
формуле S x(t) y (t)dt . Иногда эти две формулы складывают и делят на 2 так, что
формула приобретает дифференциальную форму
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
xdy ydx |
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x |
2 |
|
y |
2 |
|
|
|
|
|
|
|
|
|
||
Пример 2 Найти площадь эллипса |
|
|
|
|
1. |
|
|
|
|
|
|
|||||
a |
2 |
b |
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
x a cos t |
t 0; |
2 |
|||||
Решение. Параметрическое уравнение эллипса |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
y b sin t, |
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
cos 2t |
|
|
ab |
|
|
||
S / 2 b sin t ( a sin t)dt ab |
dt |
|
S |
|||||||||||||
|
2 |
2 |
||||||||||||||
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вычисление площади в полярной системе координат. |
|
|
|
|
|
|||||||||||
ОПР. Элементарной областью Ф |
на плоскости называют фигуру, |
|||||||||||||||
1 и 2 , кривой r r( ), 1; 2 |
. |
|
|
|
|
|
|
|
||||||||
. Тогдаab
ограниченную лучами
ФОРМУЛА вычисления площади в полярной системе координат.
Если функция r r( ) непрерывна на отрезке 1; 2 , то площадь области по формуле
Ф
вычисляется
ДОК. Пусть 0 , 1,..., n
|
1 |
|
2 |
|
|
S |
|
r |
2 |
( ) |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
- разбиение отрезка
d
1
. |
|
|
|
; 2 . Пусть k |
|
min |
r( ) и |
|
|
k 1 ; k |
|

k |
|
max |
|
r( ) . Тогда объемлющей фигурой для Ф |
||
|
|
|
k 1 |
; |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
ограниченная кусочно-постоянной функцией |
r r ( ) |
является элементарная Ф область,
|
k |
, |
k 1 |
; |
k |
, |
и лучами |
|
|
|
|
||||
|
k 1,2,...,n |
|
|
||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
1 и 2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
, имеющая площадь S |
2 |
k k |
. Объемлемой фигурой дляФ |
является |
||||||||||||||
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
элементарная область Ф , ограниченная кусочно-постоянной функцией |
|
|
|
|
|
|
|
|||||||||||
|
, |
|
; |
|
, |
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
r r ( ) k |
|
k 1 |
|
k |
|
и лучами |
, |
|
, имеющая площадь S |
|
2 |
|
|
. |
||||
|
|
|
|
|
2 |
|
k |
|||||||||||
|
k 1,2,...,n |
|
|
|
|
1 |
|
|
|
|
k |
|
|
|||||
|
|
|
|
|
|
|
|
|
2 k 1 |
|
|
|
|
|
||||
|
|
являются интегральными суммами функции |
1 |
|
|||
Числа S |
и S |
2 |
|
|
|
|
(верхняя и нижняя интегральные суммы Дарбу, см. Пример
|
убывает, |
|
возрастает. |
||||
сумма S |
S |
||||||
Если функция |
1 |
r 2 |
( ) |
интегрируема на отрезке 1; 2 , то |
|||
2 |
|||||||
|
|
|
|
|
|
||
r |
2 |
( ) |
на отрезке 1; 2 |
||
|
|||||
1). Если разбиение |
|
|
|||
|
|||||
, то
inf S |
sup S S |
|
|
1 |
||
|
|
|||||
Ф |
|
Ф |
|
|
2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Пример 3. Найти площадь одного лепестка кривой
|
|
|
|
2 |
|
|
|
|
r |
2 |
( )d . |
|
|||
|
|
||
|
|
|
|
1 |
|
|
|
r asin m |
|||
(
m
– лепестковая роза).
РЕШЕНИЕ. |
|
|
|
|
|
|
|
|
|
|
|
|
||
0, |
|
. S |
1 |
/ m a2 sin 2 m d |
a2 |
sin 2 d |
a2 |
. |
|
|
||||
2 |
|
|
|
|
|
|||||||||
1 |
m |
2 |
|
|
|
|
2m |
|
4m |
|
|
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
||
ДЛИНА дуги кривой. |
|
|
|
|
|
|
|
|
|
|
||||
ОПР. Дуга кривой |
разбивается точками Ak |
, k 1,2,...,n на n сегментов, концы которых |
||||||||||||
соединены отрезками |
A |
; A |
, образующими ломанную линию |
. Ее длина L |
зависит от |
|||||||||
|
|
|
|
|
k |
k 1 |
|
|
|
|
|
|
|
|
дуги кривой и разбиения кривой точками Ak , k 1,2,...,n |
|
|
||||||||||||
Длиной кривой называют число, равное L lim L , если оно существует. |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||

Рассмотрим дугу графика функции y f (x) на отрезке a;b . Каждому разбиению
x0 , x1 ,..., xn 1 |
отрезка a;b соответствует ломаная , состоящая из объединения |
отрезков с началом в точках |
Ak (xk ; f (xk )) и концом в точке Ak 1(xk 1; f (xk 1)) , k 0,1, 2,..., n |
||||||
|
n |
|
|
|
|
|
|
Длина L ломанной равна L |
|
2 |
xk |
|
2 |
fk , где fk f (xk ) f (xk 1 ) , xk xk xk 1. |
|
|
|
||||||
|
k 0 |
|
|
|
|
|
|
Если функция y f (x) имеет непрерывную производную на отрезке a;b , то по теореме |
|||||||
Лагранжа существует набор |
1 , |
2 ,..., n точек k xk 1; xk , для которых |
|||||
|
|
|
|
|
|
|
|
fk f ( k ) xk . Тогда длина ломанной |
|
|
|
|
|||
L |
|
n |
x |
|
f ( |
|
) |
x |
|
|
|
n |
1 f ( |
|
) |
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
|
|
2 |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
k |
|
k |
|
|
k |
|
|
|
k |
|
|
|
k |
|
||
|
|
k 1 |
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
является интегральной суммой непрерывной функции (x) |
1 f |
|
2 |
||||||||||||||||
|
(x) |
||||||||||||||||||
и поэтому
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L lim L |
|
1 f |
|
2 |
dx (*) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
0 = |
(x) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ФОРМУЛА вычисления длины кривой, заданной через параметр. |
|
|
|
|
|
|
|||||||||||||||||||||
Если дуга кривой задана параметрическими уравнениями |
|
x x(t), |
t ; |
|
, x (t) 0 |
|
|||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y y(t) |
|
|
|
|
|
|
|
в которых функции x(t), |
y(t) имеют непрерывные производные, то |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
2 |
|
|
|
|
2 |
dt . |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x (t) y (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для ее доказательства сделаем в интеграле (*) замену |
x x(t), t ; |
. Тогда |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
y (t) |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
y (t) |
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
f (x) |
2 |
|
|
|
|
|
|
|
x (t) |
2 |
y (t) |
2 |
|
||||||||||
f (x) |
, dx x (t)dt |
|
|
|
|
|
|
|
|
|
|
x (t)dt |
|
|
|||||||||||||
|
и 1 |
|
dx |
|
1 |
|
|
|
|
|
|
|
|
dt |
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
x (t) |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
x (t) |
|
|
|
|
|
|
|
|
|
||
ФОРМУЛА вычисления длины кривой, заданной в полярной системе.
Если r r( ) , 1; 2 - уравнение кривой в полярной системе координат, то
x r cos r( ) cos , |
|
|
|
|
|
|
|||||
. Тогда x r ( ) cos r( )sin |
и y r ( )sin r( ) cos |
||||
y r sin r( )sin . |
|
|
|
|
|
Вычислим x ( ) 2 y ( ) 2 r( ) 2 r ( ) 2 и получим искомую формулу
2
L 
 r( ) 2 r ( ) 2 d .
r( ) 2 r ( ) 2 d .
1
.

Пример 4. (длина цепной линии)
Вычислить длину дуги, заданной уравнением
y chx,
x
0;
b
.
РЕШЕНИЕ

 1 y 2
1 y 2
|
1 sh |
2 |
x chx |
|
b |
|
L chxdx shx |
b |
0 |
|
0 |
|
shb
.
УПРАЖНЕНИЕ. Область ограничена графиком непрерывно дифференцируемой функции y f (x), x a,a h и прямой, проходящей через точки A(a; f (a)) и B(a h; f (a h))
(сегмент криволинейной трапеции). Доказать, что ее площадь S (h) o(h2 ) .
РЕШЕНИЕ
f (x) f (a)
|
, |
2 |
a; a |
1 |
|
|
f h
(a h) f (a) |
(x a) |
|
h |
||
|
||
. Тогда |
|
f ( 1 )(x a)
f ( |
2 |
)(x a) ( f ( ) |
|
1 |
f
( |
2 |
))(x a) |
|
|
, где
S(h) |
a h |
f ( ) f ( ) (x a)dx |
|
(h) |
(x a)2 |
x a h |
|
|
(h) |
h2 |
o(h2 ) , где (h) - |
|||
a |
f |
|
|
f |
|
|||||||||
|
1 |
|
2 |
|
2 |
|
|
2 |
f |
|||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
x a |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функция колебания для производной |
f |
|
|
|
|
|
|
|
||||||
(x) на отрезке a,a h . Из предположения о |
||||||||||||||
непрерывности f |
|
|
|
|
|
|
|
|
|
|
|
|
||
(x) следует, что f (h) o(1) . |
|
|
|
|
|
|
||||||||
ВОПРОСЫ К ЭКЗАМЕНУ.
1.Доказательство формулы для вычисления площади криволинейной трапеции.
2.Доказательство формулы для вычисления площади фигуры, ограниченной кривой, заданной через параметр. Вычисление площади фигуры, граница которой задана уравнением в полярной системе координат.
3.Длина дуги кривой заданной графиком функции, параметрическими уравнениями,
уравнением кривой в полярной системе.
