4.Розрахункова частина. Розробка асу тп та структурної схеми системи управління

4.1 Ідентифікація об'єкта

Метою ідентифікації є отримання математичного опису об'єкта. Ідентифікація може бути проведена аналітичними або експериментальними методами. В аналітичних методах фізичні закони аналізуються і застосовуються при аналізі процесів, що відбуваються в об'єкті. В експериментальних методах необхідні дані, наприклад криві прискорення, отримують безпосередньо з об'єкта. Для перевірки достовірності аналітично отриманих моделей використовуються експериментальні методи.

Аналітичне визначення математичної моделі - контроль температури теплообмінника, який охолоджує дріжджі, є важливим аспектом виробництва пекарських дріжджів. Є кілька причин, чому це необхідно:

1. контроль активності дріжджів: температура має значний вплив на активність дріжджів. Підтримання оптимальної температури під час охолодження дріжджів забезпечує належну реакційну здатність і здатність до бродіння. Невідповідний температурний режим призводить до зниження якості та продуктивності дріжджів.

2. зупинка процесу розмноження. Охолодження дріжджів в теплообміннику знижує температуру після активного розмноження і бродіння. Це зупиняє процес бродіння і зберігає бажані властивості дріжджів для використання у виробництві.

3. контроль якості продукту. Правильна температура охолодження дріжджів важлива для забезпечення якості кінцевого продукту. Недостатнє охолодження може призвести до розростання дріжджів під час зберігання, що може вплинути на структуру та смак хлібного виробу.

4. енергоефективність: контроль температури теплообмінника, який охолоджує дріжджі, також важливий для енергоефективності виробничого процесу. Оптимізація температурного режиму дозволяє знизити енерговитрати і забезпечити ефективну роботу системи охолодження.

Розглянемо теплообмінник, схематично зображений на рис.4.1.

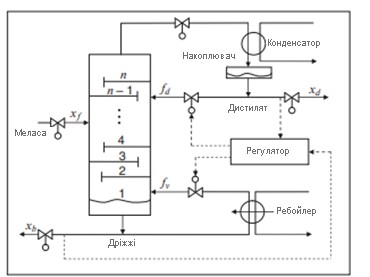
Рисунок 4.1 - Принципова схема теплообміннику

Алгоритм визначення передаточної функції:

1. визначаємо час нормованої кривої розгону, який відповідає значенню h = 0,7 й позначаємо його t7. По кривій даний час дорівнює 483 секунди.

2. Інтервал ділимо на 3 частини. Опустимо перпендикуляр до кривої розгону й визначаємо величину hH4. Відповідно до кривої hH4 = 0,33.

3. Маємо зв'язок між точками кривої розгону й параметрами моделі, а саме t 7 = 1,2 (T 1+T 2).

4. Щоб знайти постійні часу об'єкта управління застосовується допоміжна величина Z2, із номограми.

Рисунок 4.2 – Графік кривої розгону

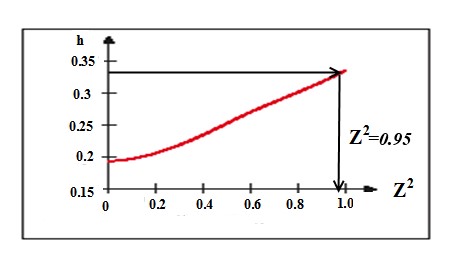
Рисунок 4.3 - Номограма для отримання величини Z²

5. Визначаємо постійних часу об'єкта управління T1 і T2:

Т1=t⁷ (1+ z)

T₂ = t⁷ (1− z)

𝑇₁ = (1 + 0.975) = 448.5 с

𝑇₂ = (1 − 0.975) = 5.67 с

Т.к. T₁ >>T ₂, переходимо до моделі першого порядку: ^1+Tp

Передаточна функція буде мати вигляд:

𝑊(𝑝) =

Отримані криві розгону перевіримо на адекватність. Для цього використаємо метод Фішера [8]. Ділимо весь інтервал часу на 10 частин й визначимо Y_{i зад} і Y_iмод. Дані значення наведені в таб.4.1

Таблиця 4.1– Отримані значення

зад Y	0.103	0.199	0.282	0.357	0.427	0.486	0.542	0.59	0.632	0.672
мод Y	0.102	0.2	0.28	0.353	0.425	0.484	0.54	0.584	0.631	0.67
t	50	100	150	200	250	300	350	400	450	500

Усер.мод=0,427 Усер.зад=0,429

Для розрахунків використаємо математичний пакет MathCad.

Рисунок 4.4 - MathCad розрахунки.

По таблиці для f1 = 10, f2 = 10 визначаємо критерій Фішера. Для даних значень він дорівнює 2,98. Так як по таблиці Фішера даний критерій менше ніж критерій по таблиці (1,008 <2.98), то припустимо, що ця модель адекватна.

4.2 Алгоритм роботи системи

Вибір типу регулятора і його настроювальних параметрів Для цього застосовуємо математичний пакет MATLAB. Вигляд зібраної схеми регулювання наведений на рис. 4.5.

Рисунок 4.5 - Модель в математичному пакеті MATLAB

Під час вибору регулятора для системи управління ми будемо розглядати промислові П, ПІ й ПІД - регулятори. Головними критеріями при виборі будуть час регулювання й перегулювання. Для зручності, нижче наведена таблиця із параметрами усіх регуляторів. Підбір параметрів регулятора виконується методом переміщення відповідного повзунка. Результати всіх дослідів зведено до таб. 4.2.

Таблиця 4.2 – Результати регулювання

Регулятор	P	I	D	Час регулювання, с	Перерегулювання,%
Безперервний паралельний ПІ – регулятор	14	0,07	0	72,5	5
Безперервний ідеальний ПІ – регулятор	16,93	0,004	0	65,3	3
Безперервний ідеальний П- регулятор	178,1	0	0	7,84	0
Дискретний ідеальний ПІ – регулятор	18,18	0,005	0	57,7	4
Дискретний паралельний ПІ – регулятор	17,41	0,07	0	64,2	3
Безперервний ідеальний ПІД – регулятор	12,11	0,007	6,93	275	8
Дискретний ідеальний ПІД – регулятор	16,17	0,01	6,91	226	9
Безперервний паралельний ПІД – регулятор	15,76	0,15	110,08	220	9
Дискретний паралельний ПІД – регулятор	16,17	0,16	111,89	212	8

При виборі базового регулятора звертали увагу на показники часу регулювання та перерегулювання. З усіх розглянутих варіантів найкращим вибором з точки зору цих показників буде П-регулятор. Проте моделювання із зазначеними параметрами робить це теоретично можливим, але технічно неможливим для реалізації.

При використанні ПІ-регулятора були отримані такі результати: середній час налаштування 65 с, перерегулювання 4%. ПІД-регулятори мають недоліки, зокрема необхідність налаштування трьох параметрів (що ускладнює процес), чутливість до перешкод так само, як і ПІ-регулятор.

Дивлячись на таблицю 4.2, було обрано дискретний ідеальний ПІ-регулятор. Це пов'язано з тим, що він має найкращі показники в порівнянні з іншими варіантами, наведеними в таблиці 4.2.