
- •В.Г. НОВИКОВ
- •ВВЕДЕНИЕ .................................................................
- •ТЕМА 5. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В
- •ВВЕДЕНИЕ
- •1.1. Введение
- •MatLab\ TOOLBOX\ CONTROL.
- •1.2. Ввод и преобразование моделей
- •sysd=c2d(sys, Ts, method).
- •2.1. Введение
- •h= freqs (b,a,w).
- •4.2. Моделирования процессов в линейных нестационарных и нелинейных динамических системах с использованием подсистемы MatLab SIMULINK
- •СПРАВКА
- •5. 1. Введение
- •5. 2. Пример имитационного моделирования процессов с использованием подсистемы MatLab SIMULINK
- •СПРАВКА
- •Использованные источники
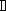
45
к циклу (7) и из “малого”, и из “большого”, то его называют устойчивым. Частные случаи устойчивых и неустойчивых циклов представлены на рисунке 4.
В случае устойчивого цикла фазовые траектории «навиваются» на эллипс, а в случае неустойчивого - уходят от него в ноль или в бесконечность.
4.2. Моделирования процессов в линейных нестационарных и нелинейных динамических системах с использованием подсистемы MatLab SIMULINK
4.2.1. Приведениелинейногодифференциальногоуравнениякканоническойформе
Исследованию нестационарных процессов предшествует предварительное преобразованиесистемы дифференциальных уравненийк стандартномувиду – к форме Коши.
Покажем один из способов такого преобразования. В результате такого преобразования система уравнений приводится к канонической форме, удобной для представления в виде эквивалентной структурной схемы, привычной при исследовании систем автоматического управления.
Пусть дифференциальное уравнение порядка n в операторной форме, описывающее процессы
1 |
+ b m −1 |
1 |
|
|
1 |
+ b 0 |
1 |
|
в системе, |
||
y( t ) = ( bm |
|
|
1+ |
... + b |
|
|
|
)z( t ), |
представл |
||
p n − m |
p n −m +1 |
p n −1 |
p n |
||||||||
ено в
виде:
(20)
где p = d/dt – символ дифференцирования; x(t), y(t) – вход и выход системы;
ai , bj– коэффициенты полиномов, в общем случае функции времени; i = [1 – n]; j = [1 – m]; m ≤ n.
Правую часть выражения (20) умножим и поделим на pn (pn / pn) и получим:
|
|
y( t ) = ( b |
1 |
|
+ |
b |
|
− |
|
1 |
+ ...+ b |
|
1 |
+ b |
1 |
|
)z( t ), |
(21) |
|||||||||
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
m |
|
pn −m |
|
1 |
pn |
−m +1 |
1 |
|
pn −1 |
0 |
|
pn |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z( t ) = |
pn x( t ) |
|
|
|
, (22) или |
z(t )= x(t )−(a |
|
1 +...+a |
1 |
|
+a 1 )z(t ). |
(23) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n−1 p |
|
1 pn−1 |
0 pn |
|
||||||||||
|
pn + an−1 |
pn−1 + ...+a p + ao |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полученныезависимости (21)- (23)являются представлением исходного уравнения
(20) в канонической форме.
Используя эти зависимости, а именно - (21) и (23) – легко может быть получена эквивалентная структурная схема, моделирующая данную систему, которая представлена на рисунке 5.
46
y(t)
 . . .
. . .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bm |
|
1 |
|
|
|
|
|
b1 |
|
|
b0 |
|||
x(t) |
z(t) |
|
|
|
|
|
|
|
|
. . . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. . . |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
|
|
a0 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. . . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рисунок 5 – Эквивалентная структурная схема системы, соответствующая дифференциальному уравнению (20)
Приведем примеры использования описанногометода представления дифференциальных уравнений.
Пример 1.
Интегро - дифференцирующее динамическое звено описывается следующим операторным уравнением (первого порядка):
|
|
|
|
|
|
|
|
y ( t ) = |
T 1 |
p + 1 |
x ( t ). |
(24) |
||
|
|
|
|
|
|
|
|
T 2 |
p + 1 |
|||||
|
Приведем его к стандартной форме (20) |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
y ( t ) = |
b 1 |
p + b 0 |
x ( t ), |
(25) |
||
|
|
|
|
|
|
|
|
p + a 0 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
b 1 |
= |
T 1 |
, b 0 = |
1 |
, |
a 0 |
= |
1 |
. |
|
|
|
|
|
T 2 |
T 2 |
T 2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
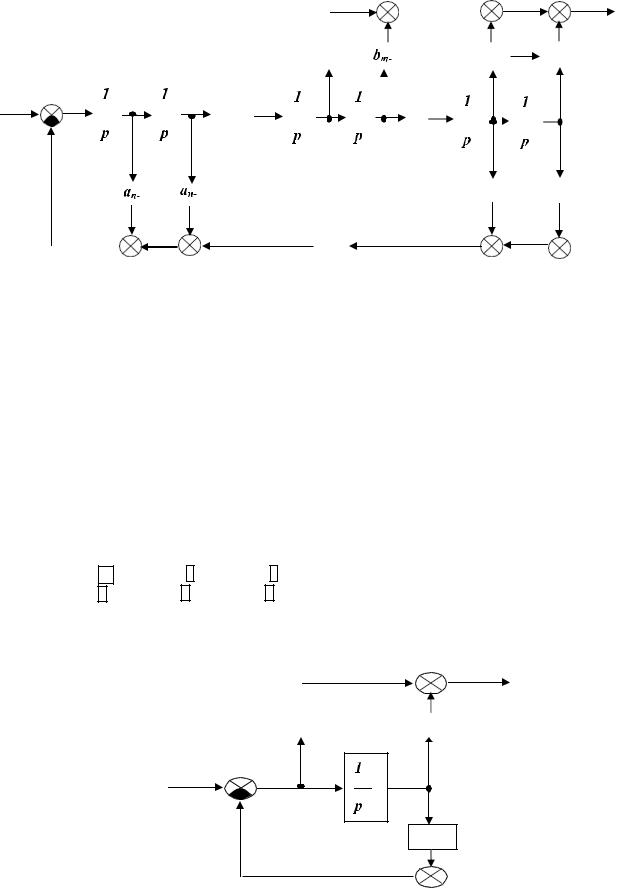
Соответствующая структурная схема, реализующая данное уравнение и получаемая из схемы для общего случая (см. рисунок 5), имеет вид:
y(t)
b1 |
|
b0 |
|
|
|
x(t) z(t)
a0
Рисунок 6 – Структурная схема, реализующая дифференциальные уравненияинтегро-дифференцирующегозвенапервого
Пример 2.
Дано операторное уравнение второго порядка:
47
|
y ( |
t ) = |
|
T |
2 p 2 |
|
+ 2 T ξ p + 1 |
|
|
x ( |
t |
). |
|
(26) |
|||||||||||
|
1 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
T |
|
2 p 2 |
+ 2 T ξ p + 1 |
|
|
|
|
|
|
|
|
|
|
|||||||
Этим уравнением моделируются динамические характеристики инерционного и |
|||||||||||||||||||||||||
форсирующего звеньев второго порядка. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Преобразуя, приведем его к стандартной форме и получим |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
y ( t |
) = |
|
b 2 |
p |
2 |
+ |
b 1 |
p |
+ |
b o |
|
|
x ( |
t |
), |
|
(27) |
|||||
|
|
|
|
|
p |
2 |
+ |
a |
p |
+ |
a |
o |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
2 T |
ς |
|
|
|
1 |
|
|
|
|
2 T ς |
|
|
|
|
1 |
|
|||||
|
T 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
b = |
1 |
, |
b = |
1 |
1 |
, |
|
b = |
|
, |
a |
= |
|
|
|
|
|
, |
a = |
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2 |
T 2 |
1 |
|
T 2 |
|
0 |
|
T 2 |
|
|
1 |
|
|
T 2 |
|
|
|
0 |
T 2 |
||||||
Соответствующая структурная схема, получаемая из схемы для общего случая (см. рисунок 5), имеет вид, представленный на рисунке 7.
y(t)
b2 |
|
b1 |
|
b0 |
x(t) z(t)
|
a1 |
|
a0 |
|
|
|
|
|
|
Рисунок 7 – Структурная схема, реализующая дифференциальные уравнения инерционного и форсирующего звеньев второго
4.2.2. Примерисследованиянестационарныхи нелинейныхпроцессов
4.2.2.1. Постановказадачи
Провести исследование нестационарной системы, замкнутая структурная схема которой представлена на рисунке 8.
При этом:
•оценить переходные процессы при задании на вход контура слежения
скачкообразного, а также синусоидальногосигналов;
• построить фазовыетраектории ошибки . |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
U1 |
|
|
U2 |
|
U3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
K0(t) |
|
|
|
W1(s) |
|
|
|
|
W2(s) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 8 – Структурная схема исследуемой модели |
|||||||||
W |
|
= |
T1 ( t )s +1 |
; W = |
K1 ( t ) , T2 = 0.05 c. |
|
|
|
|
|||||
1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
48
T2 s +1 |
2 |
s |
|
|
Таблица 1. Исходные данные
49
t, c |
0 |
5 |
10 |
20 |
35 |
50 |
Ko |
10 |
9 |
7 |
5 |
5 |
5 |
T1, c |
1.0 |
0.8 |
0.6 |
0.5 |
0.5 |
0.5 |
K1,1/c |
1 |
0. 9 |
0.7 |
0. 5 |
0.4 |
0.4 |
Как следует из рассмотрения приведенных данных, большинство параметров системы является функцией времени. Кроме того, в системе присутствует нелинейность.
Синусоидальный входной сигнал имеет вид: x=A sin (2π f t + ϕ0), A = 0.3, f=0.5 Гц, а скачкообразный сигнал – единичную ступеньку.
4.2.3. Методика формирования модели в системе MatLab (подробную методику
моделирования в среде SIMULINK Matlab см. ниже после Табл. 3).
1). В командном окне MatLab (Command Window) зададим все исходные данные модели, представленные выше, как переменные во времени (из таблицы), так и постоянные:
>> t=[0 3 10 20 35 50] >> K0=[10 9 7 5 5 5 ]
>> T1=[1 0.8 0.6 0.5 0.5 0.5]
>> K1=[1 0.9 0.7 0.5 0.4 0.4] >> T2=2.5
2). Используя подсистему SIMULINK системы MatLab, “наберем” каждое звено исходной структурной схемы.
• Усилительноезвено с переменным передаточным коэффициентом K0 (t)
Дляэтого понадобятсяследующие блоки библиотеки:
- из раздела блоков Look-Up Table (блоки задания таблиц):
- блок Look-Up Table |
- для задания одномерной таблицы (в виде |
функции одной переменной); |
|
- из раздела блоков M a t h |
Op e ra t i on s (блоки элементов, определяющих |
математические операции):
- блок GAIN, Matrix Gain – усилитель (выполняет умножение входного сигнала на постоянный коэффициент)
 ;
;
- блок Product - блок умножения и деления (выполняет вычисление произведения текущих значений сигналов)
 ;
;
– блок Sum – сумматор (выполняет вычисление сумы текущих значений)
 ;
;
- из раздела S ou r ce s (блоки источников сигналов):
- Clock - источник времени (формирует сигнал, величина которого на каждом шаге равна текущему времени моделирования)
 .
.
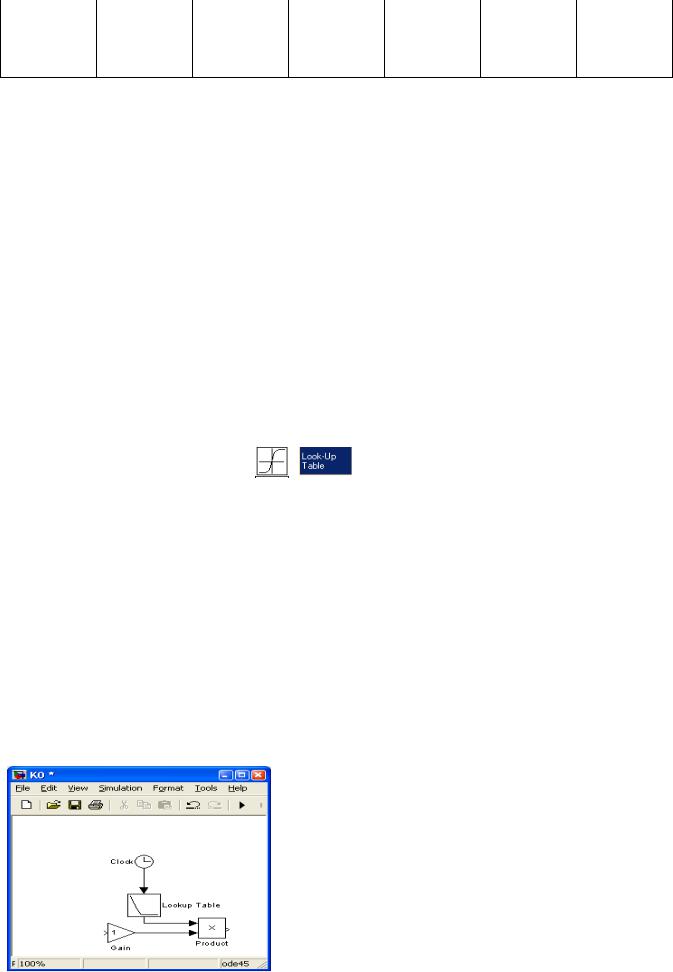
Схема имеет вид, представленный на рисунке 9.
Примечание. Для обеспечения удобства чтения схем при размещении блоков в структурной схеме использован поворот отдельных блоков относительно
Рисунок9 – Структурнаясхема, реализующая переменный коэффициент передачи
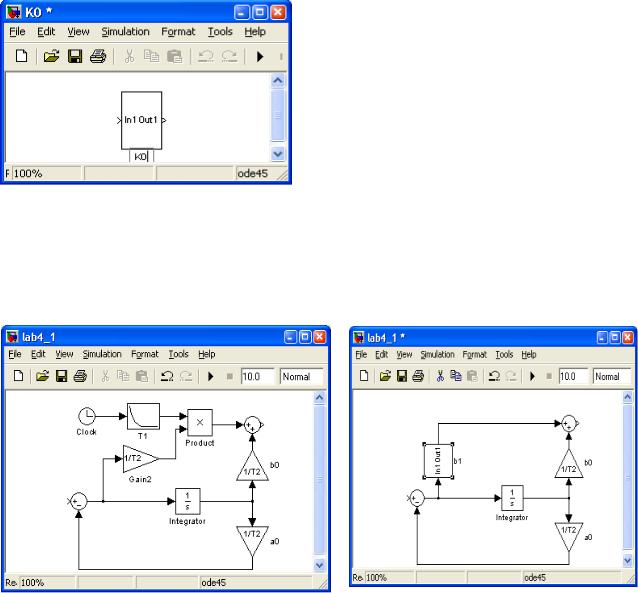
50
исходного направления. По умолчанию SIMULINK задает направление вход – выход слева направо. (На рисунке изменено направление размещения блока Clock – источник времени и блока Look-Up Table - задание одномерной таблицы).
Данная операция выполняется следующим образом.
выделяется блок (левой кнопкой мыши) щелчком правой кнопки вызывается контекстное
меню в подменю Format активизируется опция Rotate Block (поворот блока на 900), для изменения направления размещения (поворота на 1800) можно использовать опцию Flip Block.
Для уменьшения количества одновременно отображаемых на экране блоков, представленную схемуможносвести к одномуотдельномублоку– к подсистеме. Проделаем данную операцию с полученной схемой для формирования коэффициента K0.
С этой целью:
левой кнопкой мыши, не отпуская, выделяются все блоки (см. рисунок 9) правой кнопкой вызывается контекстное меню из этого меню выбирается опция Create Subsys-
|
tem по этой опции все блоки выделяются в |
|||
|
одну подситем для удобства можно |
|||
|
изменить название подсистемы. |
|
||
|
Результат |
такого |
объединения |
|
|
представлен на рисунке 10. |
|
|
|
|
Примечание. |
Состав подсистемы можно |
||
|
восстановить двумя щелчками левой кнопки мыши |
|||
|
•Интегро-дифференцирующее звено |
W1 |
||
Рисунок10 – Подсистема, объединяющая |
с переменной постоянной времени T1(t) |
|
||
Приведенное |
на схеме |
(см. рисунок |
8) |
|
блоки формирования коэффициента K0 |
операторное выражение W1 представим в виде |
|||
|
||||
структурной схемы, которая будет |
аналогична представленной на |
рисунке 6.Схема, |
||
реализующая указанное звено, примет вид, представленный на рисунке 11. |
|
|
||
Для удобства группублоков на рисунке 11, формирующих переменный коэффициент b1 можно объединить в один и присвоить имя b1.
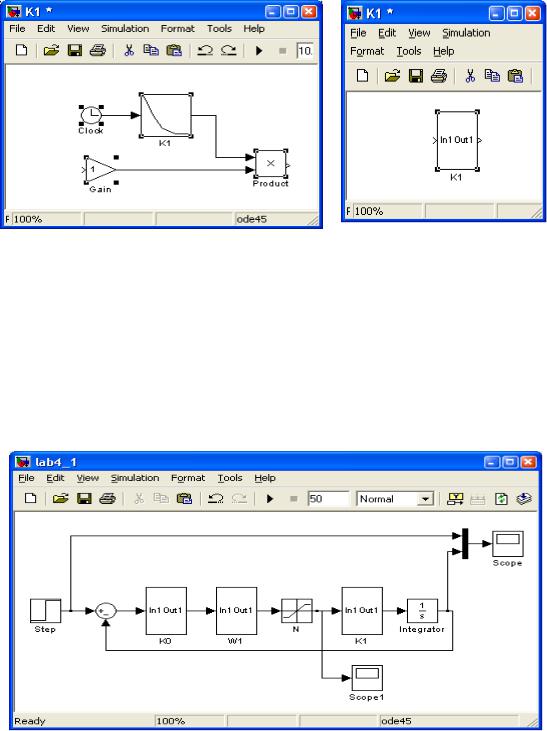
Рисунок 11 – Схема звена W1 |
Рисунок 12 – Схема звена W1 c объединенными |
блоками |
Результат представлен нарисунке 12.
• Усилительноезвено с переменным передаточным коэффициентом K1 (t)
Звено “набирается” таким же образом, как и звено K0 (t). Результирующая схема представлена на рисунке 13.
51
Рисунок13 – Схема набора коэффициента |
Рисунок 14 –Коэффициент |
||
передачи K1 |
(t) в одном блоке |
||
передачи K1 (t) |
|||
|
|
||
После последующего объединения блоков схемы в один блок получим соответствующую подсистему, приведенную на рисунке 14.
3). Соединениевсех звеньев в соответствии с исходной структурной схемой.
Помимо набранных выше звеньев с переменными коэффициентами дополним модель
нелинейностью N (типа“насыщение”  ), интегратором
), интегратором 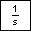 , а также сумматором
, а также сумматором  . Итоговая схема для моделирования в нашем случае может выглядеть так, как это
. Итоговая схема для моделирования в нашем случае может выглядеть так, как это
представлено на рисунке 15.
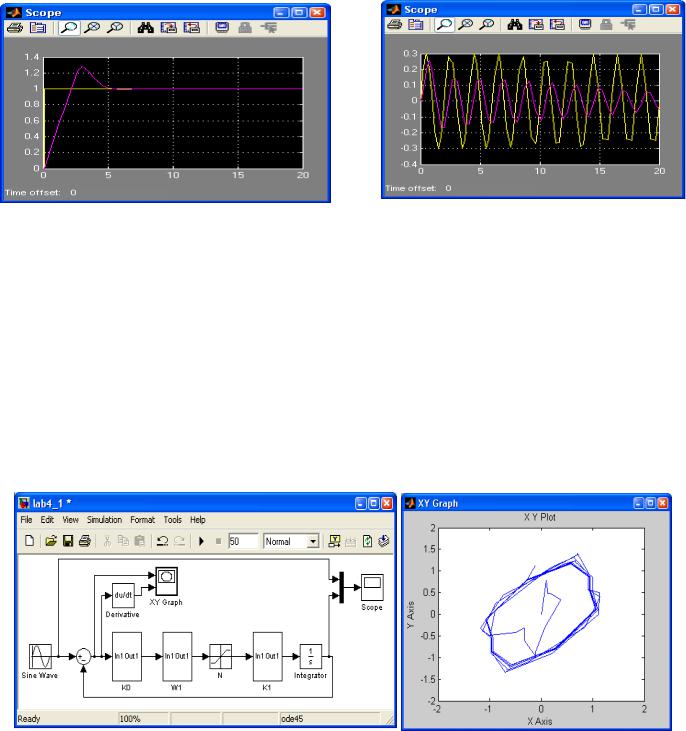
Рисунок 15 – Итоговая схема для исследования
4). Исследование системы.
Для исследования процессов можно использовать любой из способов представления графиков:
-либо осциллографа Scope;
-либографопостроитель XY Graf;
-блок записи в рабочую область MatLab To Workspase исследуемых переменных на
выходе нужного блока с последующим построением графиков с использованием оператора plot.
52
4.2.2.3. Пример результатовисследования Оценим отработкусистемой входных сигналов:
-единичная ступенька;
-синусоидальный сигналсзаданными параметрами.
Уровень ограничения заданной нелинейности типа “насыщение” для определенности ограничим уровнем 0.5.
Результаты моделирования в виде переходных процессов на выходе приведены на рисунках 16 и 17.
Рисунок 16 – Процессы на выходе |
Рисунок 17 – Процессы на выходе системы при |
системы приступенчатом скачке на входе |
синусоидальном сигнале на входе |
Как следует из рассмотрения рисунка 17, амплитуда выходного сигнала уменьшается с течением времени, что вызвано переменностью коэффициента передачи K0, K1 во времени.
Получим фазовую |
траекторию ошибки |
при задании на |
входе синусоидального |
сигнала A sin(ω*t) при A=1 и ω=1/рад/c. |
|
|
|
Для этого, как сказано выше, необходимо иметь помимо ошибки скорость dΔ/dt. Ее |
|||
легко получить, если |
воспользоваться блоком вычисления |
производной Derivative |
|
 из группы блоков Continuous.
из группы блоков Continuous.
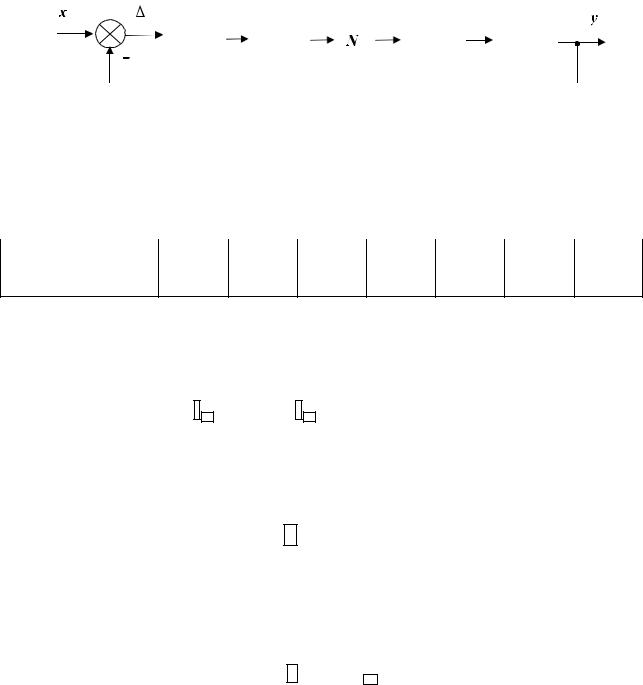
На рисунке 18 приведена схема (аналогичная представленной на рисунке 15), снабженная блоком вычисления производной. А на рисунке 19 – фазовая траектория ошибки dΔ/dt=f(Δ).
Рисунок 18 – Схема для получения фазовой траектории |
Рисунок 19 – Пример фазовой траектории |
53
4.3.Заданиенасамостоятельнуюработу
4.3.1.Исходнаясистема
Дана нестационарная и нелинейная система, структурная схема которой представленная на рисунке 20.
|
|
|
Uвх |
|
Uупр |
|
||
|
|
|
|
|
|
|
|
|
Wкф(s) |
|
Kус(t) |
|
|
|
WОУ(s) |
|
Wкз(s) |
Рисунок 20 – Структурная схема исследуемой модели
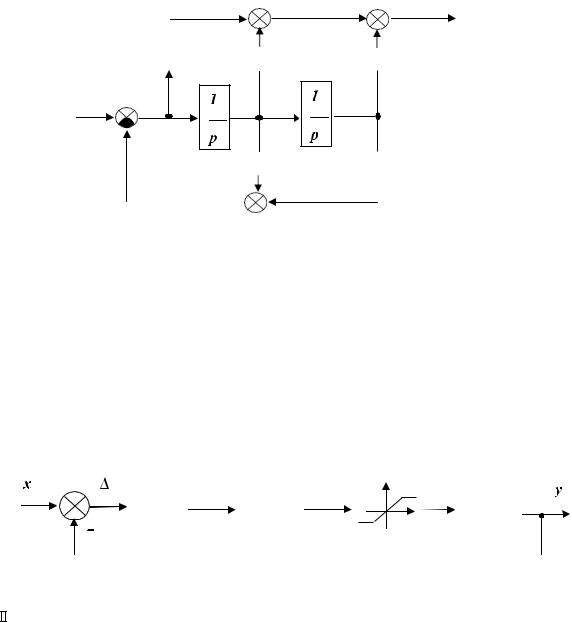
где x, y – вход и выход системы; Wi (s) – операторные выражения передаточных функций системы; – ошибка регулирования; N – нелинейное звено.
Исходные параметры системы для различных вариантов заданы в таблицах 2 и 3.
4.3.2. Требования к работе
4.3.2.1. “Набрать ” модель с использованием пакета SIMULINK. Таблица2. Характеристики объекта управления
t, c |
0 |
2 |
5 |
8 |
10 |
14 |
20 |
KОУ, м/с |
10 |
60 |
80 |
50 |
40 |
20 |
14 |
fОУ,Гц |
1.0 |
4.2 |
5.0 |
4.0 |
2.7 |
2.3 |
1.8 |
Характеристикидинамическихзвеньевопределяютсяследующимивыражениями:
•Корректирующее звено:
Wкф ( s ) = |
T1 s +1 |
|
, |
(28) |
||
(T2 s + 1 )(T2 s + 1 ) |
||||||
|
|
|
|
|||
где T1 ( t ) = [ 0.0123 f |
ОУ3 − 0.1339 f ОУ2 + 0.2328 |
f ОУ |
+ 1.2177 ] , |
|||
(29) |
|
|
|
|
|
|
а fОУ (t) – из таблицы 2, T2 и T3 - из таблицы 3. |
|
|
|||
• Переменноеусилительноезвено: |
+1.429 f |
|
− |
||
K ( t ) = 5 |
{ 0.0407 f 3 |
+0.2931 f 2 |
|
||
ОУ |
ОУ |
|
ОУ |
|
|
|
|
|
|||
УС |
KОУ ( t ) |
|
где KОУ(t), fОУ (t) – известные зависимости из таблицы 2.
•“Нестационарный” объект управления:
W ( s ) = |
KОУ ( t ) |
2.165} , (30)
, |
(31) |
|
|
|
|
ОУ |
T 2 |
s 2 |
+ 2T |
О |
ξ |
s + 1 |
|
|
|
|
|
ОУ |
|
|
ОУ |
|
|
где TОУ |
( t ) = |
|
1 |
, |
|
|
|
|
|
(32) |
2π |
fОУ ( t ) |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
а KОУ(t) – из таблицы 2, ξОУ – из таблицы 3.
• Кинематическое звено |
1 . |
|
W ( s ) = |
(33) |
где
54
к |
|
|
|
|
|
|
|
|
|
ый зависимостью |
|
|
|
|
s |
Uвых = kн F( Uвх ) , |
(34) |
||
2 |
||||
• Н |
|
|
|
|
F( Uвх ) - нелинейность типа насыщение с порогами ограничения на уровне ±1; |
|
|||
е
л
и
н
е
й
н
о
е
з
в
е
н
о
N
–
о
д
н
и
м
и
з
д
в
у
х
в
и
д
о
в
-
п
е
р
в
ы
й
,
о
п
р
е
д
е
л
я
е
м
|
55 |
|
kн – коэффициент передачи до ограничения сигнала, kн = 0.20; |
|
|
- второй, определяемый зависимостью |
|
|
Uвых |
= F sin( 0.0625 π Uвх ) , |
(35) |
где F - нелинейность типа |
”насыщение” с порогами ограничения на уровне |
±8, |
ограничивающий входной сигналUвх.
Рекомендация: При формировании нелинейности второго типа воспользуйтесь блоком
Trigonometric Function  из раздела блоков M a t h O p e r at i on s .
из раздела блоков M a t h O p e r at i on s .
4.3.2.2.Провести исследование системы при задании на вход:
•скачкообразного и
•гармонического сигнала x=Aвх sin (2π fвх t) при двух значениях частоты: fвх=0.5 Гц и fвх=1 Гц с заданной амплитудой Aвх.
При этом провести анализ качества процессов на выходе системы:
-перерегулирование;
-время переходногопроцесса;
-построить фазовыетраектории.
4.3.2.3.Результаты представить в виде графиков.
4.3.3.Отчетность
4.3.3.1.Результаты исследований сохранять в личной папке в соответствующем M-
файле.
4.3.3.2.По работе оформить отчет в виде Пояснительной записки в текстовом
процессоре MS Word:
-на электронном носителе;
-на бумажном носителе.
56
Таблица 3. Варианты исходных параметров системы
№ |
Входной |
Фильтр Wкф(s) |
Kус(t) |
N, |
Объект управления |
|
||||
вариа |
сигнал |
|
|
|
|
в |
|
WОУ(s) |
|
|
|
|
|
|
|
|
соответст |
|
|
|
|
нта |
Aвх |
T1, с, |
T2, с |
T3, с |
|
вии с |
KОУ(t) |
TОУ, с, |
|
ξОУ |
|
|
|
|
|
|
выражени |
|
|
|
|
1 |
0.30 |
|
0.04 |
0.005 |
|
(3ем4) |
|
|
|
0.4 |
2 |
0.45 |
|
0.05 |
0.005 |
|
(35) |
|
|
|
0.3 |
3 |
0.55 |
|
0.06 |
0.005 |
|
(34) |
|
|
|
0.2 |
4 |
0.30 |
2 |
0.07 |
0.005 |
2 |
(35) |
|
2 |
|
0.6 |
5 |
0.45 |
0.08 |
0.005 |
(34) |
|
|
0.6 |
|||
таблицей |
таблицей |
|
таблицей |
|
||||||
6 |
0.55 |
0.09 |
0.005 |
|
(2) |
|
|
|||
|
|
(35) |
|
|
|
0.5 |
||||
7 |
0.65 |
|
0.10 |
0.005 |
|
(34) |
|
|
|
0.4 |
8 |
0.75 |
(29)выражениемссоответствииви |
0.04 |
0.005 |
(30)выражениемссоответствииви |
(35) |
|
(32)выражениемссоответствииви |
|
0.3 |
9 |
0.85 |
0.05 |
0.004 |
(34) |
таблицейссоответствииВ |
|
0.2 |
|||
21 |
0.85 |
0.10 |
0.004 |
(34) |
|
0.3 |
||||
10 |
0.90 |
|
0.06 |
0.003 |
|
(35) |
|
|
|
0.1 |
11 |
1.00 |
|
0.07 |
0.004 |
|
(34) |
|
|
|
0.4 |
12 |
1.20 |
|
0.08 |
0.007 |
|
(35) |
|
|
|
0.3 |
13 |
0.30 |
|
0.09 |
0.009 |
|
(34) |
|
|
|
0.2 |
14 |
0.45 |
|
0.10 |
0.010 |
|
(35) |
|
|
|
0.6 |
15 |
0.55 |
|
0.04 |
0.004 |
|
(34) |
|
|
|
0.6 |
16 |
0.30 |
|
0.05 |
0.003 |
|
(35) |
|
|
|
0.5 |
17 |
0.45 |
|
0.06 |
0.004 |
|
(34) |
|
|
|
0.4 |
18 |
0.55 |
|
0.07 |
0.007 |
|
(35) |
|
|
|
0.3 |
19 |
0.65 |
|
0.08 |
0.009 |
|
(34) |
|
|
|
0.2 |
20 |
0.75 |
|
0.09 |
0.010 |
|
(35) |
|
|
|
0.1 |
|
|
|
|
|
|
|
|
|
|
|
22 |
0.90 |
|
0.04 |
0.003 |
|
(35) |
|
|
|
0.2 |
23 |
1.00 |
|
0.05 |
0.004 |
|
(34) |
|
|
|
0.1 |
24 |
1.20 |
|
0.06 |
0.007 |
|
(35) |
|
|
|
0.2 |
25 |
1.00 |
|
0.07 |
0.005 |
|
(34) |
|
|
|
0.1 |
