
- •В.Г. НОВИКОВ
- •ВВЕДЕНИЕ .................................................................
- •ТЕМА 5. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В
- •ВВЕДЕНИЕ
- •1.1. Введение
- •MatLab\ TOOLBOX\ CONTROL.
- •1.2. Ввод и преобразование моделей
- •sysd=c2d(sys, Ts, method).
- •2.1. Введение
- •h= freqs (b,a,w).
- •4.2. Моделирования процессов в линейных нестационарных и нелинейных динамических системах с использованием подсистемы MatLab SIMULINK
- •СПРАВКА
- •5. 1. Введение
- •5. 2. Пример имитационного моделирования процессов с использованием подсистемы MatLab SIMULINK
- •СПРАВКА
- •Использованные источники
18
ТЕМА 2. ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ ПРИ ИССЛЕДОВАНИИ СИСТЕМ с помощью пакета MatLab “Signal Processing Toolbox”
2.1. Введение
Цифровая обработка сигналов включает в себя создание средств численного преобразования массива заданного (измеренного в дискретные моменты времени) процесса изменения некоторой непрерывной физической величины с целью извлечения из него полезной информации о другой физической величине, содержащейся в измеренном сигнале.
Общая схема образования измеряемого сигнала и процесса его преобразования в целях получения информации о величине, которая должна быть измерена, представлена на рисунке.
Полезный сигнал
Первичныйпреобразователь
Измеряемая величина |
Шум |
Измеритель |
|
Измереннаявеличина |
Шум измерителя |
Дискретныйпреобразователь
(экстраполятор + АЦП)
Массив измерений Шум дискретизации
Фильтр
Обработанная информация
Фильтр на рисунке служит для преобразования входного дискретного во времени сигнала в выходной с минимизацией искажений, вызванных шумами.
Пакет MatLab Signal Processing Toolbox позволяет:
-рассчитывать конкретные числовые характеристики цифровых и аналоговых фильтровпотребуемым АФЧХ;
-формировать последовательности типовых временных сигналов;
-обрабатывать их припомощи спроектированных фильтров.
2.2.Общиесредствафильтрации.Формированиеслучайныхпроцессов
2.2.1.Общиеосновы линейной фильтрации
Фильтрация – этопреобразование заданного сигнала с помощью линейного фильтра. Рассмотрим основы линейной фильтрации на примере линейного стационарного
фильтра второго порядка, передаточная функция которого имеет вид:
|
|
|
|
|
|
|
19 |
|
y( s ) |
= |
|
|
A |
, |
(1) |
W ( s ) = |
x( s ) |
|
|
|
|||
s |
2 |
+ 2ςω0 s +ω02 |
|||||
|
|
|
|
|
|
где x -заданный процесс;
y – получаемый на выходе фильтра процесс; ω0 – частота собственных колебаний фильтра;
ξ – относительный коэффициент затухания этого фильтра.
Для контроля и графического представления передаточной функции любого динамического звена удобно использовать процедуру freqs.
В общем случае обращение к ней имеет вид:
h= freqs (b,a,w).
При этом процедура создает вектор h комплексных значений частотной характеристики W(jω) по передаточной функции W(s), заданной векторами коэффициентов ее числителя (b) и знаменателя (a), а также по заданному векторуw частоты ω. Если аргумент w не задан, то выбирается 200 отсчетов частоты, для которых вычисляется частотная характеристика.
Пример.
A=1; ξ=0.05; T0 = 2π / ω0=1.
Вычислим значения коэффициентов числителя и знаменателя и выведем графики АЧХ и ФЧХ:
>>T0=1;dz=0.05;
>>om0=2*pi/T0;a=1
>>A=1;
>>a1(1)=1;a1(2)=2*dz*om0;a1(3)=om0^2;b1(1)=A;
>>freqs(b1,a1)
Magnitud
Phase(degrees)
100 |
|
|
10-2 |
|
|
10-4 |
101 |
102 |
100 |
||
|
Frequency (rad/s) |
|
0 |
|
|
-50 |
|
|
-100 |
|
|
-150 |
|
|
-200 |
101 |
102 |
100 |
Frequency (rad/s)
Дискретная передаточная |
функция, |
соответствующая непрерывному фильтру (1) |
||||
(которая может быть полученапутемZ - преобразованияразностного уравнениядискретного |
||||||
аналога дифференциального уравнения), имеет вид: |
||||||
G( z ) = y( z ) = |
ATs2 |
, |
(2) |
|||
|
x( z ) |
|
a0 + a1 z −1 + a2 z −2 |
|
|
|
где a0 =1+2 ξ (ω0 Ts)+ (ω0 Ts)2; |
|
|
|
|||
a1 = -2 (1+ξ (ω0 Ts)); |
|
|
|
|||
a2 =1.
Вобщем случае дискретная передаточная функцияимеет вид: |
||||||||
|
y( z ) |
|
b |
+b z −1 |
+ ...+b |
z −m |
||
G( z ) = |
|
|
= |
0 |
1 |
m |
|
(3) |
|
|
|
|
|
||||
|
x( z ) |
|
a0 |
+ a1 z −1 |
+ ...+a nz −n |
|||

20
В системе MatLab фильтрация сигнала, описываемого дискретной передаточной функцией вида осуществляется процедурой filter следующим образом:
y= filter(b, a, x)
где x – заданный вектор значений входного сигнала;
y – вектор значений выходного сигнала фильтра, получаемого вследствие фильтрации; b – вектор коэффициентов числителя дискретной передаточной функции (1);
a – вектор коэффициентов знаменателя дискретной этой функции.
Пример
Полезный сигнал имеет синусоидальную форму с известным периодом T1 =1 c и амплитудой A1 = 0.75. сформируем этот сигнал как вектор его значений в дискретные моменты времени с дискретом Ts=0.001 c:
>>Ts=0.001;
>>t=0:Ts:20;
>>A1=0.75; T1=1;
>>Yp=A1*sin(2*pi*t/T1);
>>plot(t,Yp),grid;
>>title('P-signal');
>>xlabel('t, c');
>>ylabel('Yp')
Y
P-signal
0.8 |
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-0.2 |
|
|
|
|
|
|
|
|
|
|
-0.4 |
|
|
|
|
|
|
|
|
|
|
-0.6 |
|
|
|
|
|
|
|
|
|
|
-0.8 0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
|
|
|
t, c |
|
|
|
|
|
Пусть вследствие прохождения через преобразователь и в результате измерения к полезному сигналу добавились шумы:
-более высокочастотная синусоида с периодом T2 =0.2 c и амплитудой A2=10;
-белый гауссовский шум измерителя с интенсивностью Aш=5.
Врезультате создается такой измеренный сигнал x(t):
>>T2=0.2;A2=10; eps=pi/4;
>>Ash=5;
>>x=A1*sin(2*pi*t/T1)+A2*sin(2*pi*t/T2+eps)+Ash*randn(1,length(t));
>>plot(t,x), grid
>>title('input')
>>xlabel('t, c')
>>ylabel('x(t)')

21
x(t)
input
30
20
10
0
-10
-20
-300 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
|
|
|
t, c |
|
|
|
|
|
Требуется так обработать измеренные данные x, чтобы восстановить по ним полезный процесс как можно точнее.
Т.к. частота полезного сигнала заранее известна, восстановление его можно выполнить при помощи резонансного фильтра вида (2). При этом необходимо создать такой фильтр,чтобыпериодегособственныхколебанийTфбылравенпериодуколебанийполезного сигнала (Tф= T1).
Чтобы после прохождения через такой фильтр амплитуда восстановленного сигнала совпадала с амплитудой полезного сигнала, нужно входной сигнал фильтра домножить на постоянную величину 2ξω0 2 (поскольку при резонансе амплитуда выходного сигнала уменьшается именно во столько раз по сравнению с амплитудой входного сигнала).
Сформируемфильтр,описанный выше:
>>T1=1; Tf=T1;dz=0.05;
>>om0=2*pi/Tf;A=1;oms=om0*Ts;
>>a(1)=1+2*dz*oms+oms^2;
>>a(2)= - 2*(1+dz*oms);
>>a(3)=1;
>>b(1)=A*Ts*Ts*(2*dz*om0^2);
Пропустимсформированныйпроцессчерез него:
>>y=filter(b,a,x);
>>plot(t(10002:end),y(10002:end),t(10002:end),Yp(10002:end)),grid
>>title('procesOut(Tf=1,dz=0.05)');
>>xlabel('t, c');
>>ylabel('Y(t)')
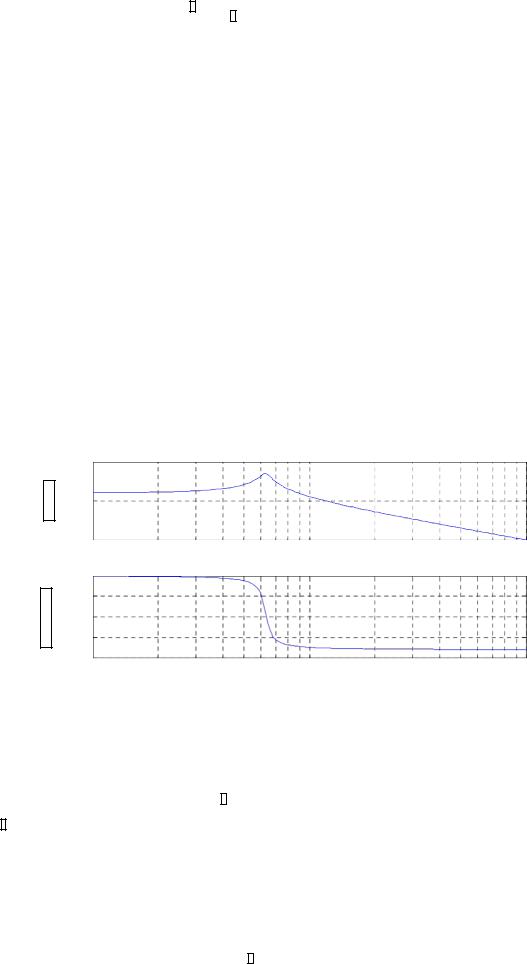
Врезультате получим процесс, приведенный на рисунке.
Y(t)
procesOut(Tf=1,dz=0.05)
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
|
|
|
t, c |
|
|
|
|
|
Из рисунка можно заметить два недостатка:
22
-восстановленный процесс устанавливается на выходе фильтра только спустя некоторое время вследствие нулевых начальных условий самого фильтра как динамического звена;
-в установившемся режиме наблюдается значительный сдвиг фаз (π/2) между восстанавливаемым и восстановленным процессами.
Дляизбежанияфазовыхискаженийполезногосигналаприеговосстановленииможно воспользоваться процедурой двойной фильтрации – filtfilt , которая осуществляет обработку вектора в два приема: сначала в прямом, а затем в обратном направлении.
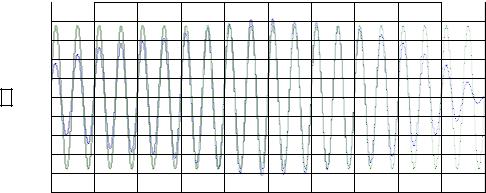
Результатпредставлен ниже.
>>y=filtfilt(b,a,x);
>>plot(t,y,t,Yp),grid;
>>title('procedure FILTFILT (Tf=1,dz=0.05)');
>>xlabel('t, c');
>>ylabel('Y(t)')
Y(t)
procedure FILTFILT (Tf=1,dz=0.05)
1
0.8 |
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-0.2 |
|
|
|
|
|
|
|
|
|
|
-0.4 |
|
|
|
|
|
|
|
|
|
|
-0.6 |
|
|
|
|
|
|
|
|
|
|
-0.8 |
|
|
|
|
|
|
|
|
|
|
-10 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
|
|
|
t, c |
|
|
|
|
|
2.2.2. Формированиеслучайныхпроцессов
Сформировать случайный процесс с заданной корреляционной функцией можно,
если:
-сначала сформировать случайный процесс, являющийся нормально распределеннымбелымшумом,
-а затем “пропустить его через некоторое динамическое звено (формирующий
фильтр)”.
На выходе такого звена получается нормально распределенный случайный процесс с корреляционной функцией, вид которой определяется типом формирующего фильтра.
Белый гауссовый шум в MatLab образуется при помощи процедуры randn.
Для этого достаточно задать дискрет времени Ts, образовать с этим шагом массив (вектор) t моментов времени в нужном диапазоне, а затем сформировать по указанной процедуре вектор-столбец длиной, равной длине вектора t.
Например
>>Ts=0.01;
>>t=0:Ts:20;
>>x1=randn(1,length(t));
>>plot(t,x1),grid;
>>title('Gaus(T=0.01c)');
>>xlabel('t, c');
>>ylabel('X1(t)')
Соответствующийпроцессимеет вид:
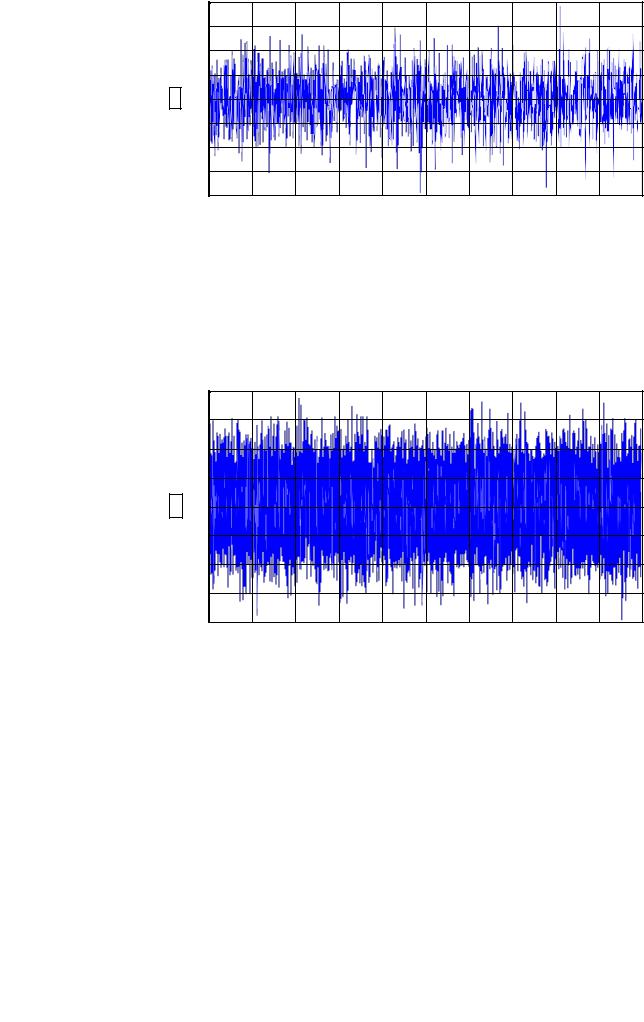
23
X1(t)
Gaus
4 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
-3 |
|
|
|
|
|
|
|
|
|
|
-40 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
|
|
|
t, c |
|
|
|
|
|
Для другого дискрета Ts=0.001с имеем
>>Ts=0.001;
>>t=0:Ts:20;
>>x2=randn(1,length(t));
>>plot(t,x2),grid;
>>title('Gaus Ts=0.001 c');
>>xlabel('t, c');
>>ylabel('X2(t)')
X2(t)
Gaus Ts=0.001 c
4
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
|
-3 |
|
|
|
|
|
|
|
|
|
|
-40 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
|
|
|
t, c |
|
|
|
|
|
Создадим дискретный формирующий фильтр второго порядка с частотой собственных колебаний ω0 = 2π рад\с =1 Гц и относительным коэффициентом колебаний затухания ξ=0.05 по выражениям (2) коэффициентов:
>>om0=2*pi;dz=0.05;A=1;oms=om0*Ts;
>>a(1)=1+2*dz*oms+oms^2;
>>a(2)=-2*(1+dz*oms;
>>a(3)=1;
>>b(1)=A*2*dz*oms^2;
Пропустимобразованный процессx1 через созданный формирующийфильтр:
>> y1=filter(b,a,x1);
Построим соответствующий график:
24
Y1(t)
procedure (T0=1;dz=0.05;Ts=0.01)
0.04
0.03 |
|
|
|
|
|
|
|
|
|
|
0.02 |
|
|
|
|
|
|
|
|
|
|
0.01 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-0.01 |
|
|
|
|
|
|
|
|
|
|
-0.02 |
|
|
|
|
|
|
|
|
|
|
-0.03 |
|
|
|
|
|
|
|
|
|
|
-0.04 |
|
|
|
|
|
|
|
|
|
|
-0.050 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
|
|
|
t, c |
|
|
|
|
|
Аналогичныеоперациипроизведем спроцессомx2(t)
>>x2=randn(1,length(t));
>>Ts=0.001;
>>om0=2*pi;dz=0.05;A=1;oms=om0*Ts;
>>a(1)=1+2*dz*oms+oms^2;
>>a(2)=-2*(1+dz*oms);
>>a(3)=1;
>>b(1)=A*2*dz*oms^2;
>>y2=filter(b,a,x2);t=0:Ts:20;
>>plot(t,y2),grid;
>>title('procedure (T0=1;dz=0.05;Ts=0.001)');
>>xlabel('t, c');
>>ylabel('Y1(t)')
Y1(t)
procedure (T0=1;dz=0.05;Ts=0.001)
0.08
0.06 |
|
|
|
|
|
|
|
|
|
|
0.04 |
|
|
|
|
|
|
|
|
|
|
0.02 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-0.02 |
|
|
|
|
|
|
|
|
|
|
-0.04 |
|
|
|
|
|
|
|
|
|
|
-0.060 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
|
|
|
t, c |
|
|
|
|
|
Как видим, на выходе формирующего фильтра действительно образуется случайный колебательный процесс с преобладающей частотой 1 Гц.
2.3.Спектральныйистатистическийанализ
2.3.1.Основныепонятия
Основная задача спектрального анализа сигналов – выявление гармонического спектра этих сигналов, т.е. определение частот гармонических составляющих сигнала (выявление частотного спектра), амплитуд этих гармонических составляющих
(амплитудного спектра) и их начальных фаз (фазового спектра).
В основе спектрального анализа лежит теория Фурье о возможности разложения
любого периодическогопроцессанасчетную суммуотдельных гармоническихсоставляющих.

25
Процедуры fft и ifft осуществляют преобразования заданного вектора,
соответствующие дискретному прямому(fft – Fast Fourier Transformation) и обратному (ifft
– Invers Fast Fourier Transformation) преобразованиям Фурье.
Обращение к этим функциям y=fft(x,n);x=ifft(y,n)
приводит к формированию вектора y в первом случае, и вектора x - во втором, по формулам:
y( k ) = ∑n x( m )e − j 2π( m −1 )( k −1 ) / n
m1=1 n
j 2π( m −1 )( k −1 ) / n
x( m ) = |
∑y( k )e |
(4) |
|
n k =1 |
|
где n – число элементов заданного вектора x; j – мнимая единица.
2.3.2. Примерыспектральногоанализа
Входной сигнал представим в виде вектора, элементы которого равны значениям функции, являющейся суммой двух синусоид с частотами 5 и 12 Гц. Найти Фурьеизображение этого сигнала и вывести графики входного процесса и модуля его Фурьеизображения:
>>t=0:0.001:2;
>>x=sin(2*pi*5*t)+cos(2*pi*12*t);
>>plot(t,x),grid;
>>title('input');
>>xlabel('t, c');
>>ylabel('X(t)')
X(t)
input
2 |
|
|
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-0.5 |
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
-1.5 |
|
|
|
|
|
|
|
|
|
|
-20 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
1.2 |
1.4 |
1.6 |
1.8 |
2 |
|
|
|
|
|
t, c |
|
|
|
|
|
>>y=fft(x);
>>a=abs(y);
>>plot(a);grid;
>>title('fourier');
>>xlabel('number');
>>ylabel('absF(X(t))')
26
fourier
1200
1000
800
absF(X(t)
600
400
200
0 0 |
500 |
1000 |
1500 |
2000 |
2500 |
|
|
|
number |
|
|
Теперь осуществимобратноепреобразованиес помощью функции ifft:
>>z=ifft(y);
>>plot(t,z), grid;
>>title('inverse');xlabel('number');
>>xlabel('t, c');
>>ylabel('Z(t))')
Z(t)
inverse
2 |
|
|
|
|
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-0.5 |
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
-1.5 |
|
|
|
|
|
|
|
|
|
|
-20 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
1.2 |
1.4 |
1.6 |
1.8 |
2 |
|
|
|
|
|
t, c |
|
|
|
|
|
Как следует из последнего рисунка, воспроизведенный процесс в точности совпадает с исходным.
Из выражений (4) можно заметить:
- номер m соответствует моменту времени tm , в который измерен входной сигнал
x(m);
-номер k – это индекс значения частоты fk, которому соответствует найденный элемент y(k) дискретногопреобразованияФурье;
-для перехода от индексов к временной и частотной областям, необходимо знать значение шага h дискрета времени, через который измерен входной сигнал x(t), и промежуток T времени, на протяжении которого он измерен; тогда дискрет по частоте в изображении Фурье определяется выражением
Df=1/T,
а диапазон изменения частоты – выражением
F=1/h.
Так в нашем примере Df=0.5, F= 1000.
-Фурье - изображение определяется функцией fft только для положительных частот
вдиапазоне от 0 до F, что неудобно для построения графиков Фурье – изображения от частоты; более удобным является переход к вектору Фурье – изображения, определенному в диапазоне частот [-F/2 - F/2].
Сформируем для данного примера массив частот и выведем график с аргументом
частотой
>> f=0:0.5:1000; >> plot(f,a)'grid;
>> plot(f,a);grid;
27
>>title('F(x)');xlabel('friquency, Hz');
>>ylabel('abs(F(X))')
abs(F(X)
F(x)
1200
1000
800
600
400
200
0 0 100 200 300 400 500 600 700 800 900 1000 friquency, Hz
На рисунке трудно различить частоты (5 и 12 Гц), с которыми колеблется входной
сигнал.
Для установления истинного спектра входного сигнала необходимо вначале преобразовать полученный вектор y Фурье – изображения с помощью процедуры fftshift. Она предназначена для формирования нового вектора z из заданного у путем перестановки второй половины вектора у в первую половину вектора z
>>f1=-500:0.5:500;
>>v=fftshift(y);
>>a=abs(v);
>>plot(f1(970:1030),a(970:1030));grid;
>>title('F/N');
>>xlabel('friquency,Hz');
>>ylabel('abs(F(X))/N')
1200 |
|
|
|
F/N |
|
|
|
|
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
|
800 |
|
|
|
|
|
|
|
sab(F(X)/N |
|
|
|
|
|
|
|
600 |
|
|
|
|
|
|
|
400 |
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
0 |
-15 |
-10 |
-5 |
0 |
5 |
10 |
15 |
-20 |
|||||||
|
|
|
friquency, Hz |
|
|
|
|
Из графика видно, что в спектре входного сигнала есть две гармоники- 5 и 12 Гц. Неудобным является то, что по графику невозможно определить амплитуду этих
гармоник. Чтобы сделать это, необходимо весь вектор y разделить на число его элементов N:
>>N=length(y);
>>a=abs(v)/N;
>>plot(f1(970:1030),a(970:1030));grid;
>>title('F/N');
>>xlabel('friquency,Hz');
>>ylabel('abs(F(X))/N')

28
abs(F(X)/N
F/N
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0 |
-15 |
-10 |
-5 |
0 |
5 |
10 |
15 |
-20 |
friquency, Hz
2.4.Заданиенасамостоятельнуюработу
2.4.1Цифроваяобработка сигналов
Провести цифровую обработкусигналовсистемы.
На выходе системы измеряемый сигнал x(t) представляет собой сумму трех сигналов:
x(t) = x0(t) + x1(t) + xш(t),
где x0(t)=A0 sin[(2π/T0) t] - измеряемый (полезный) сигнал; x1(t) = A1 sin[(2π/T1) t] – регулярный шум преобразователя; xш(t) – шум измерений, с интенсивностью Aш.
Подобрать дискретный фильтр второго порядка вида (2) с параметрами Aф, ξф при условии, что период его собственных колебаний равен периодуколебаний полезного сигнала, а выделяемый сигнал максимально воспроизводит полезный сигнал.
Представитьвсесоответствующиеграфики.
2.4.2. Формированиеслучайного процесса из белого шума
Сформировать случайный процесс из белого шума, используя формирующий фильтр второго порядка вида (2) с частотой собственных колебаний fфф и относительным коэффициентом колебаний затухания ξфф.
Представитьвсесоответствующиеграфики.
2.4.3. Формированиепроцесса как сумма гармоник
Сформировать процесснавыходесистемыследующего вида:
x(t) = x2(t) + x3(t) + x4(t),
где x2(t)=A2 sin[(2π*f2* t]; x3(t)=A3 sin[(2π*f3* t]; x4(t)=A4 sin[(2π*f4*t];
Выполнить спектральный анализ сигнала на выходе системы.
2.4.4. Исходныеданные
Исходные параметры для исследований для каждого варианта заданы в таблице.
2.4.5. Отчетностьполабораторнойработе
Результатыисследований для отчетаоформить втекстовомпроцессореWord.
29
|
|
|
|
|
|
|
|
|
|
Формирование |
|
|
|
|
|
|
|
|
№ |
Ts |
|
|
|
Фильтрация |
|
|
случайного |
|
Спектральный анализ |
|
Примечание |
||||||
варианта |
|
|
|
|
|
|
|
|
процесса |
|
|
|
|
|
|
|||
|
|
A0 |
T0,с |
A1 |
|
T1 с |
Aш |
Aф |
ξф |
fфф,Гц |
ξфф |
A2 |
A3 |
A4 |
f2,Гц |
f3,Гц |
f4,Гц |
|
1 |
2 |
3 |
4 |
5 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
1 |
0.01 |
1 |
2 |
10 |
|
1 |
5 |
1 |
0.05 |
5 |
0.05 |
1 |
2 |
3 |
1 |
3 |
4 |
|
2 |
0.01 |
1 |
2 |
10 |
|
1 |
5 |
1 |
0.05 |
5 |
0.05 |
1 |
2 |
3 |
1 |
4 |
5 |
|
3 |
0.01 |
1 |
3 |
10 |
|
1 |
5 |
1 |
0.05 |
5 |
0.05 |
1 |
3 |
5 |
1 |
5 |
4 |
|
4 |
0.01 |
2 |
1 |
5 |
|
2 |
6 |
1 |
0.05 |
5 |
0.05 |
1 |
2 |
3 |
1 |
4 |
3 |
|
5 |
0.001 |
2 |
0.5 |
5 |
|
2 |
7 |
1 |
0.02 |
2 |
0.02 |
1 |
2 |
3 |
1 |
3 |
6 |
|
6 |
0.001 |
2 |
0.5 |
5 |
|
2 |
8 |
1 |
0.02 |
2 |
0.02 |
1 |
3 |
5 |
1 |
2 |
5 |
|
7 |
0.001 |
3 |
1 |
15 |
|
1 |
5 |
2 |
0.02 |
2 |
0.02 |
2 |
4 |
7 |
2 |
1 |
4 |
|
8 |
0.001 |
3 |
0.5 |
15 |
|
1 |
5 |
2 |
0.02 |
5 |
0.02 |
2 |
4 |
8 |
2 |
0.5 |
3 |
|
9 |
0.001 |
3 |
0.5 |
15 |
|
1 |
5 |
2 |
0.01 |
5 |
0.01 |
2 |
5 |
9 |
2 |
3 |
2 |
|
10 |
0.001 |
0.9 |
1 |
10 |
|
2 |
5 |
1 |
0.01 |
5 |
0.01 |
1 |
2 |
3 |
1 |
4 |
4 |
|
11 |
0.002 |
0.9 |
2 |
10 |
|
2 |
6 |
1 |
0.05 |
5 |
0.05 |
1 |
2 |
3 |
1 |
5 |
5 |
|
12 |
0.002 |
0.9 |
2 |
10 |
|
2 |
7 |
1 |
0.05 |
2 |
0.05 |
1 |
3 |
5 |
1 |
4 |
4 |
|
13 |
0.002 |
0.75 |
3 |
5 |
|
1 |
8 |
1 |
0.05 |
2 |
0.05 |
1 |
2 |
3 |
1 |
3 |
3 |
|
14 |
0.002 |
0.75 |
1 |
5 |
|
1 |
5 |
1 |
0.05 |
2 |
0.05 |
1 |
2 |
3 |
1 |
2 |
6 |
|
15 |
0.002 |
0.75 |
0.5 |
5 |
|
1 |
5 |
1 |
0.02 |
6 |
0.02 |
1 |
3 |
5 |
1 |
1 |
5 |
|
16 |
0.005 |
0.8 |
0.5 |
15 |
|
1 |
5 |
2 |
0.02 |
7 |
0.02 |
2 |
4 |
7 |
2 |
0.5 |
4 |
|
17 |
0.005 |
0.8 |
1 |
15 |
|
1 |
5 |
2 |
0.02 |
8 |
0.02 |
2 |
4 |
8 |
2 |
1 |
3 |
|
18 |
0.005 |
0.8 |
0.5 |
15 |
|
1 |
6 |
2 |
0.02 |
2 |
0.02 |
2 |
5 |
9 |
3 |
2 |
2 |
|
19 |
0.005 |
0.8 |
0.5 |
7.5 |
|
2 |
7 |
1 |
0.01 |
2 |
0.01 |
1 |
1 |
2 |
3 |
3 |
4 |
|
20 |
0.005 |
1 |
1 |
7.5 |
|
2 |
8 |
1 |
0.01 |
2 |
0.01 |
1 |
1 |
3 |
1 |
2 |
5 |
|
21 |
0.005 |
1 |
2 |
7.5 |
|
2 |
5 |
1 |
0.05 |
6 |
0.05 |
1 |
1 |
4 |
1 |
1 |
4 |
|
22 |
0.005 |
1 |
2 |
7.5 |
|
1 |
5 |
1 |
0.05 |
7 |
0.05 |
1 |
1 |
4 |
2 |
0.5 |
3 |
|
30
ТЕМА 3. МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ ПРОЦЕССОВ с помощью пакета MatLab “SIMULINK”
3.1. Краткие сведенияо подсистеме MatLab SIMULINK
SIMULINK входит всоставсемейства программных продуктовсистемыMatLab. Подсистема SIMULINK служит для моделирования динамических процессов. Для
пользователя это - конструктор, с помощью которого блоки, соответствующие отдельным элементам динамической системы, объединяются в единое целое и проводится исследование поведения элементов и/или системы в целом во времени.
3.1.1. ЗапускподсистемыSIMULINK
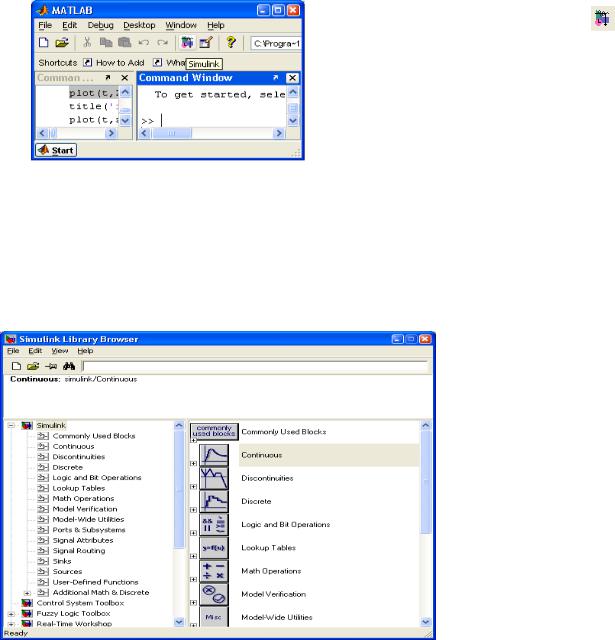
Осуществляется после предварительного запуска системы MatLab одним из трех
|
способов: |
|
|
|
- нажатием кнопки SIMULINK |
на |
|
|
панели инструментов |
системы MatLab |
|
|
(рисунок 1); |
|
|
|
- в строке командного окна MatLab |
||
|
набрать SIMULINK и нажать ENTER; |
|
|
|
- выполнить опцию OPEN в меню FILE |
||
|
и открыть файл модели ( |
mdl-файл) |
– при |
Рисунок 1 |
запуске уже готовой и отлаженной модели. |
||
При применении |
первых |
двух |
|
способовоткрываетсяокнообозревателябиблиотеки блоков(рисунок 2).
БиблиотекаблоковSIMULINK – этонаборвизуальных объектов,припомощи которых можно, соединяя модули линиями функциональной связи, составлять блок-схему любого устройства.
Библиотекаразбита на ряд разделов, основные из них перечислены ниже (по алфавиту):
•Continuous – блоки аналоговых элементов;
Ри
су
но к 2
31
• Discontinuities –
блоки нелинейных
элементов;
• Discrete - блоки дискретных элементов;
• |
Math |
Operations– |
блоки |
|
|
элементов, определяющих математические операции; |
|
• |
Signal & Routing – |
блоки |
|
32
маршрутизации сигналов;
•Sinks – блоки приема и отображения сигналов;
•Sources – блоки источников сигналов.
Блоки, входящие в раздел Sources (Источники) предназначены для формирования сигналов. Все блоки - источники имеют по одному выходу и не имеют входов.
Блоки, входящие в раздел Sinks (Приемники) предназначены для приема сигналов,
они имеют только входы и не имеют выходов.
В разделе Discrete (Дискретные элементы) содержатся блоки, с помощью которых может быть описано поведение дискретных систем.
При выборе соответствующего раздела библиотеки его содержимое отображается в правой части окна (рисунок 3).
3.1.2. Созданиемодели
Для создания модели в среде SIMULINK необходимо выполнить последовательно ряд действий.
|
1. |
|
Создать новый файл |
||
|
модели |
с |
помощью |
команды |
|
|
File/New/Model или соответству- |
||||
|
ющей кнопки на панели инстру- |
||||
|
ментов |
. |
Вновь созданное окно |
||
|
имеет вид, представленный на ри- |
||||
|
сунке 4. |
|
|
|
|
Рисунок 4 |
2. Расположить блоки в окне |
||||
модели. Для этого открыть соот- |
|||||
|
|||||
|
ветствующий раздел |
библиотеки |
|||
|
блоков и “перетащить“ нужный |
||||
|
блок при |
помощи левой клавиши |
|||
|
мыши. На рисунке 5 показано ок- |
||||
|
но модели, содержащее блоки. |
||||
3. Далее, если требуется, изменить параметры блока, установленные по умолчанию. Для
этого, указав на изображеРниисеунболко5ка, дважды щелкнуть левой клавишей мыши: откроется окнопараметров данного блока.
Пример для блока передаточной функции Transfer Fcn приведен на рисунке 6.
4. После установки на схеме всех блоков требуется их соединение.
4.1 Первый способ: - указать на “выход” блока; - нажать левую клавишу,
и, не отпуская, провести линию ко “входу” другого блока; - отпустить клавишу.
Рисунок 6
33
Примечание. Если соединение не создано, то линия связи будет пунктирной и иметь красный цвет. В случае правильного соединения линия связи будет сплошной.
4.2Второй (альтернативный)способсоединения:
-выделить блок-источник;
-затем нажать клавишуCtrl;
-выделить блок-приемник.
Для созданияточки разветвленияв соединительной линии:
-подвести курсор к предполагаемому узлу;
-и, нажав правую клавишу, протянуть линию.
5. После составления расчетной схемы необходимо сохранить по команде File / Save
As.
При этом имя файла:
-можетиметь произвольную длину;
-но должно начинаться с буквы;
-и содержать только алфавитно-цифровые символы латиницы и знаки
подчеркивания
3.1.3. Некоторыеосновныеприемы подготовки иредактированиямодели
3.1.3.1. Добавлениетекстовыхнадписей
Для повышения наглядности модели удобно использовать текстовые надписи. Для этого:
-указать мышью место надписи;
-дваждыщелкнуть левой клавишей мыши.
Также можно изменить и подписи к блокам.
Для этого установить курсор в область надписи и щелкнуть левой клавишей мыши – в подписи появится курсор ввода.
3.1.3.2. Выделение объектов
Длявыделенияодногообъекта:
Установить курсор на объекте Щелкнуть левой клавишей мыши Появятся маркеры по углам объекта.
Для выделения нескольких объектов:
Установить курсор вблизи объектов Нажать левую клавишу Удерживая ее,
перемещать мышь Появится пунктирная рамка Все охваченные рамкой объекты становятся выделенными.
3.1.3.3. Перемещение блоков и вставка блоков в соединение
Перемещение – обычным путем перетаскивания мышью. При этом соединение не разрывается, а просто сокращается или увеличивается по длине. В длинное соединение можно вставить новый блок. Такая вставка возможна лишь для блоков, имеющих один вход и один выход.
3.1.3.4. Форматирование объектов Используется для:
-управленияотображениемнадписей и видомблоков;
-установки цвета линий и цвета фона блоков, а также всего окна;
34
-форматирования надписей;
-и др.
Осуществляется при помощи опций, вызываемым:
-либо при помощи контекстногоменю(вызываемого нажатием правой клавиши);
-либо при помощи меню Format.
3.1.4. Установка параметровмоделированияи его выполнение
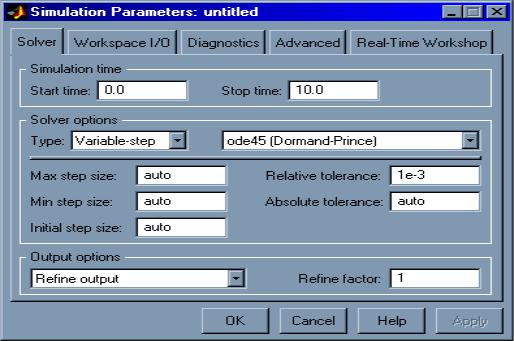
Перед выполнением моделирования необходимо предварительно задать параметры. Задание параметров выполняется в панели управления меню Simulation / Simulation
Parameters.
Вид панели управления приведен на рисунке 7.
Рисунок 7
Окно настройкипараметров моделирования имеет 4 вкладки:
•Solver (Решатель) – для установки параметров моделирования.
•Workspase I/O (Ввод/вывод данных в рабочую область) – для установки параметров обмена данными с рабочей областью MatLab.
•Dianostics (Диагностика)– для выбора параметров диагностики.
•Advanced (Дополнительно)– для установки дополнительных параметров.
•Real-Time Workshop – для задания параметров “Мастерская реального
времени”.
3.5.1. Установкапараметровмоделирования
Установка параметров моделирования выполняется с помощью элементов управления, размещенных на вкладке Solver, и они разделены на 3 группы.
Simulation time (интервал моделирования): задаются начальное (Start time) и конечное (Stop time) значения времени
Simulation options (параметры решателя): указывается метод интегрирования (Type), либо с фиксированным (Fixed-step), либо с переменным (Variable-step) шагом.

35
Можно выбрать один из следующих методов:
•ode45 – одношаговые явные методы Рунге-Кутты 4-го и 5-го порядка;
•ode23 – одношаговые явные методы Рунге-Кутты 2-го и 3-го порядка;
•ode113 – многошаговый метод Адамса - Башворта – Мултона переменного порядка;
•ode23t - метод трапеций с интерполяцией;
•и др.
Величина шага интегрирования по умолчанию устанавливается системой автоматически (auto).
При выборе Fixed-step задать режим расчета (Mode): MultiTasking (многозадачный), SinglTasking (однозадачный), Auto (автоматический выбор режима).
При выборе Variable-step задать три параметра: Max step size – максимальный шаг интегрирования, Min step size – минимальный шаг интегрирования, Initial step size – начальное значение шага интегрирования.
Output options (параметрывывода).
Для данного параметра возможен выбор одного из трех вариантов:
•Refine output (Скорректированный вывод) – позволяет изменять шаг регистрации модельного времени и тех сигналов, которые сохраняются в рабочей области MatLab с помощью блока To Workspase. При этом установка дискретности шага вывода выполняется в строке редактирования Refine factor. По умолчанию Refine factor = 1, т.е. регистрация производится для каждого значения модельного времени. При задании Refine factor = k будет регистрироваться каждое k-ое значение сигналов.
•Produce additional output (Дополнительный вывод) – обеспечивает дополнительную регистрацию параметров модели в заданные моменты времени.
•Produce specified output only (Формировать только заданный вывод) – устанавливает вывод параметров модели только в заданные моменты времени, которые
указываются в поле Output times.
3.5.2. Выполнениемоделирования
Запуск моделирования выполняется с помощью пункта меню Simulation/Start или
соответствующей кнопки |
на панели инструментов. |
|
Процесс моделирования можно завершить досрочно, выбрав пункт меню Simula- |
||
tion/Stop или соответствующей кнопки |
на панели инструментов. |
|
Моделирование также можно остановить (Simulation/Pause) и затем продолжить
(Simulation/Continue).
3.5.3. Завершение работы
Для завершения работы необходимо сохранить модель в файле, закрыть окно модели, окно обозревателя библиотеки блоков, а также командное окно системы MatLab.
3.2.Пример созданиямодели системы и выбор ее характеристик
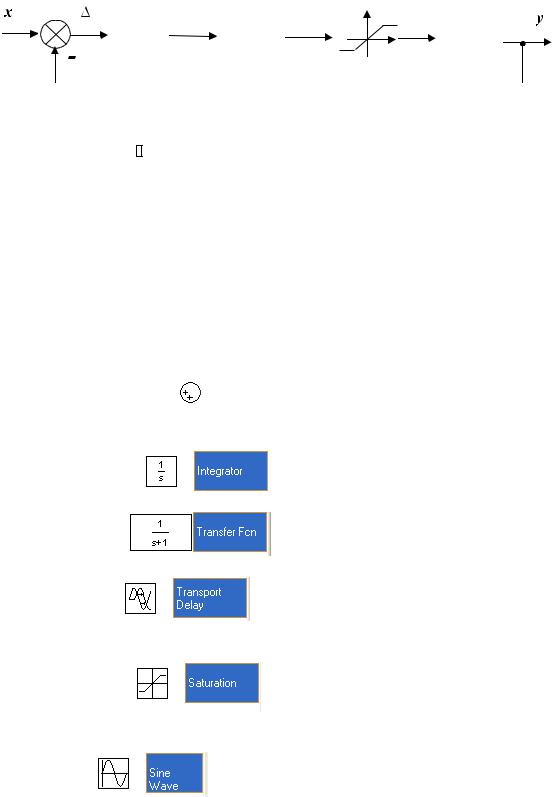
3.2.1.Постановка задачи
Создать модель следящей системы, представленной на рисунке 8 ниже, и провести ее исследование. При этом оценить переходные процессы при задании на вход контура слежения синусоидального сигнала.
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
U1 |
|
|
|
|
U2 |
|
U3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
W1(s) |
|
|
|
W2(s) |
|
|
|
|
W3(s) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 8 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
W = K exp(−sτ ) ; |
W = T1s +1 |
; |
W = |
1 |
. K1 = 3 1/c; τ= 0.2 c; T1=0.6 c; T2=0.06 c. |
|||||||||
|
||||||||||||||
1 |
1 |
|
2 |
T2s +1 |
|
3 |
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Нелинейность – типа ”насыщение”.
Синусоидальный входной сигнал имеет вид: x=A sin (2πf t + ϕ0), A = 0.3, f=0.5 Гц,
3.2.2. Методикарешения
3.2.2.1. Основныеисходныеданные
Создадим структурную схему для исследования системы. Для этого в нашем случае понадобятся следующие блоки:
- из раздела блоков M a th Op e ra t i ons (блоки элементов, определяющих математические операции):
|
– блок Sum |
; |
|
- израздела Con tinu ou s (блоки аналоговых элементов): |
|
|
- блок Integrator |
|
|
- блок Transfer Fcn – передаточная функция |
|
|
|
; |
|
- блок Transport Delay (блок фиксированной задержки сигнала) |
|
|
|
; |
- |
израздела Di s con tinui ti es (блоки нелинейных элементов): |
|
- |
Saturation - нелинейность типа “насыщение” |
|
|
|
; |
- |
из раздела Sou rc es (блоки источников сигналов): |
|
- |
Sin Wave - источник синусоидального сигнала |
|
|
|
; |
- |
Step - генератор ступенчатого сигнала |
|
 ;
;
-Clock - источник времени (формирует сигнал, величина которого на каждом шаге равна текущему времени моделирования)
 ;
;
- из раздела Sink s (блоки приема и отображения сигналов):
37
- Scope - осциллограф (построение графиков в функции времени, позволяет наблюдать за
изменением сигналов в процессе моделирования)
 ;
;
-XY Graf - графопостроитель (для построения графика значений одного сигнала в функции другого, верхний вход – для аргумента Х, нижний – для функции Y)
;
-To Workspase - блок записи в рабочую область MatLab (служит для записи данных, поступающих на вход блока в рабочую областьсистемы
MatLab)
;
- израздела Sig nal & Rou ti ng (блоки маршрутизации сигналов):
- Mux - мультиплексор (служит для объединения входных сигналов в
вектор)
 .
.
3.2.2.2. Результат составлениямодели
Созданная расчетная модель исследуемой следящей системы имеет вид, представленный на рисунке 9.
Рисунок 9
38
Как следует из рассмотрения рисунка, для анализа сигналов в процессе моделирования выходы ряда элементов снабжены блокам - приемниками Scope (осциллографами). При этом длясравнениясигналовнавходеивыходеэлементовпредварительноэтисигналыобъединены в вектор при помощи мультиплексора.
3.2.3. Результатымоделирования
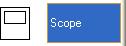
Нижепредставленысигналырегистрируемыенаосциллографах Scope: - на входе системы x и ошибки ∆ слежения (рисунок 10)
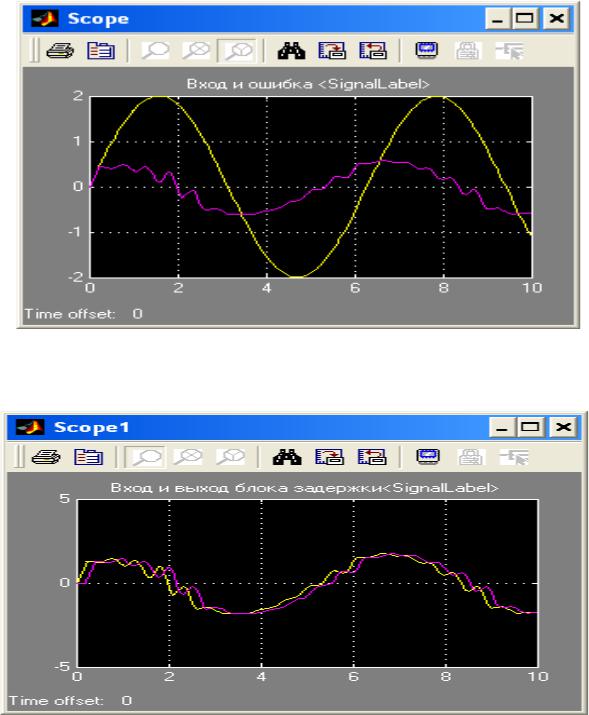
Рисунок 10 - на входе и выходе блока задержки (рисунок 11)
Рисунок 11
-на входе и выходе блока нелинейности (рисунок 12)
39
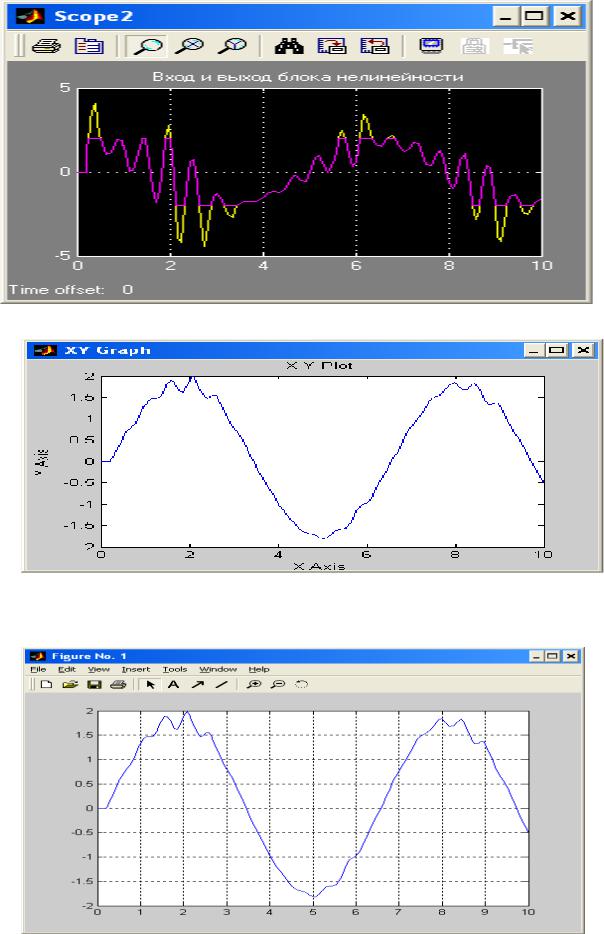
Рисунок 13 демонстрирует использованиеграфопостроителя.
Рисунок 13
На рисунке 14 представлен тот же график (с рисунка 13), но построенный по данным из рабочей области MatLab, которые записаны туда с использованием блока To Workspase
Рисунок 14

40
3.3.Заданиенасамостоятельнуюработу
3.3.1.Исходнаядинамическаясистема
Дана динамическая система, структурная схема которой представленная на рисунке
15.
|
U1 |
|
U1 |
|
|
U2 |
|
U3 |
|
W1(s) |
|
W2(s) |
W3(s) |
|
|
W4(s) |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 15
где x, y – вход и выход системы; Wi – передаточные функции звеньев; ∆ - ошибка регулирования; N – нелинейное звено.
Исходные параметры системы для различных вариантов заданы в таблице 1.
3.3.2. Требования к работе
3.3.2.1. Создание модели
Создать модель следящей системы сиспользованием аппаратаSIMULINK. 3.3.2.2. Исследование системы
Провести исследование системы. При этом:
-оценить качество переходных процессовпри заданиинавход единичногоскачкадля заданных параметров системы (величина перерегулирования, время переходного процесса); в случае неудовлетворительного качества переходных процессов подобрать
параметры корректирующего фильтра W2(s) (коэффициент усиления, постоянные времени фильтра), а также параметры нелинейного звена N (при необходимости);
-для выбранного фильтра W2(s) и нелинейного звена N выполнить исследование системы при задании на вход контура слежения синусоидального сигнала; для различных частот из заданного диапазона оценить:
-запаздываниевыходного сигнала относительно входного;
-степень усиления (ослабления) системой входного сигнала.
3.3.2.3.Отчетность
-Результатыисследований сохранять вличнойпапкевсоответствующемM-файле.
-По работе оформить отчет в виде Пояснительной записки в текстовом процессоре
MS Word:
-на электронном носителе;
-на бумажном носителе.

40
Таблица 1 Исходные параметры системы
|
W1 = K1 exp(-s τ) |
W2 = K2(T1+1)/(T2+1) |
W3 |
Нелинейность |
|
W4 |
|||
№ |
N |
|
|||||||
вариант |
K1 |
τ, c |
K2 |
T1, c |
T2, c |
|
тип |
пиктогра |
|
а |
|
мма |
|
||||||
|
|
|
|
|
|
|
|
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
10 |
0.10 |
1 |
0.2 |
0.02 |
|
Ограничитель |
|
|
2 |
5 |
0.15 |
2 |
0.3 |
0.03 |
|
Зона нечувствительности |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
0.20 |
3 |
0.4 |
0.04 |
0.1 |
Реле |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
5 |
0.25 |
2 |
0.5 |
0.05 |
Квантователь |
|
|
|
ξ = |
|
|
|||||||
5 |
10 |
0.30 |
1 |
0.6 |
0.06 |
Сухое и вязкое трение |
|
|
|
|
|
|
|
|
|
c, |
|
|
|
6 |
3 |
0.10 |
3 |
0.7 |
0.07 |
Люфт |
|
|
|
0.005 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
7 |
2.5 |
0.15 |
4 |
0.8 |
0.08 |
Ограничитель |
|
|
|
|
|
|
|||||||
8 |
2 |
0.20 |
5 |
0.9 |
0.09 |
= |
Зона нечувствительности |
|
|
|
|
|
|
|
|
3 |
|
|
|
9 |
5 |
0.25 |
2 |
1.0 |
0.10 |
Реле |
|
|
|
T |
|
1/s |
|||||||
|
|
|
|
|
|
|
|
||
10 |
4 |
0.30 |
3 |
0.2 |
0.010 |
+1); |
Квантователь |
|
|
|
|
|
|
|
|
|
|
= |
|
11 |
10 |
0.10 |
1 |
0.3 |
0.015 |
Сухое и вязкое трение |
|
||
|
4 |
||||||||
|
|
|
|
|
|
ξs |
|
|
W |
12 |
2.5 |
0.15 |
4 |
0.4 |
0.020 |
Люфт |
|
||
3 |
|
||||||||
|
|
|
|
|
|
2 T |
|
|
|
13 |
10 |
0.20 |
1 |
0.5 |
0.025 |
Ограничитель |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
14 |
5 |
0.25 |
2 |
0.6 |
0.030 |
Зона нечувствительности |
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
2 3 |
|
|
|
15 |
4 |
0.30 |
3 |
0.7 |
0.035 |
Реле |
|
|
|
1/(T |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
16 |
5 |
0.10 |
2 |
0.8 |
0.040 |
Квантователь |
|
|
|
|
|
|
|
|
|
= |
|
|
|
17 |
10 |
0.15 |
1 |
0.9 |
0.045 |
Сухое и вязкое трение |
|
|
|
3 |
|
|
|||||||
|
|
|
|
|
|
W |
|
|
|
18 |
3 |
0.20 |
3 |
1.0 |
0.050 |
Люфт |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
19 |
3 |
0.25 |
4 |
0.10 |
0.010 |
|
Ограничитель |
|
|
|
|
|
|
|
|
|
|
|
|
20 |
5 |
0.30 |
2 |
0.10 |
0.005 |
|
Зона нечувствительности |
|
|
|
|
|
|
|
|
|
|
|
|
41
ТЕМА 4. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ ДИНАМИЧЕСКИХ СИСТЕМАХ с использованием подсистемы MatLab “SIMULINK”
4.1. Краткие сведения из теории линейных нестационарных и нелинейных систем автоматического управления
Линейные стационарные системы занимают важное место в теории автоматического управления. Однако, “... образно говоря, линейные стационарные системы – (лишь) маленький островок в безграничном о к е ан е н ели не йны х и н е ст аци онар ных систем” [академик Цыпкин Я.З. -- известный советский ученый].
На практике чаще встречаются САУ, которые имеют математические модели, описываемые:
- линейными дифференциальными уравнениями с переменными коэффициентами
или
- нелинейнымидифференциальными уравнениями.
4.1.1. Особенности процессоввлинейныхнестационарныхсистемах
Линейная САУ называется нестационарной, если её параметры (коэффициенты, постоянные времени и т.п.) меняются во времени. Это обстоятельство приводит к изменению коэффициентов соответствующего дифференциального уравнения. Оно также служит признаком нестационарности системы.
Так как коэффициенты дифференциального уравнения стационарной САУ зависят от времени, то логично предположить, что от этого же времени будут зависеть все её свойства, в том числе: устойчивость, качество переходных процессов, характеристики установившегося состояния при любых типах входных воздействий.
В отличие от линейных стационарных систем, обладающих характеристическим уравнением с постоянными коэффициентами, линейные нестационарные САУ имеют характеристическое уравнение в виде нелинейного дифференциального уравнения.
Найти его корни и по ним оценить устойчивость нестационарной САУ практически невозможно даже в системе второго порядка.
Поэтомуиногда пытаются судить о свойствах нестационарной САУ по корням так называемого формального характеристического уравнения, получаемого обычным формальным путем (заменой знака дифференцирования оператором p=d/dt) из соответствующего дифференциального уравнения.
Например,длядифференциального уравнения |
|
|
2x + 4tx + 2 t 2 x + 3x = |
4 t 3 y + 6 y |
(1) |
формальноехарактеристическоеуравнениеимеетвид |
+ 3 = 0 . |
(2) |
2 p 3 + 4 t p 2 + 2 t 2 p |
Уравнение (2) позволяет в первом приближении судить о свойствах нестационарной САУ, если его коэффициенты сравнительно медленно меняются во времени. Для этого используется метод “замороженных” коэффициентов.
Данный метод используется в двух вариантах:
•“замораживание”спостояннымипараметрами;

42
•“замораживание”спеременнымипараметрами.
Впервом варианте, чтобы получить постоянные параметры, поступают, следующим образом:
- берут дифференциальное уравнениевида (1);
- задаются некоторым временем t = t0 , вблизи которого хотят узнать о свойствах
САУ;
- вычисляют коэффициенты уравнения типа (1) при t = t |
, вследствие чего приходят к |
|
0 |
дифференциальномууравнению спостоянными коэффициентами.
Далее, по этомудифференциальному уравнению судят о всех свойствах нестационарной САУ вблизи точки t = t0 .Эти суждения тем ближе к истине, чем
медленнееменяются вовремени коэффициенты уравнения(1).
Во втором варианте (“замораживание” с переменными параметрами) за
характеристическое уравнение нестационарной САУ берут уравнение вида (2). Его корни будут уже функциями времени. Если они медленно меняются во времени, то информация о поведении САУ во времени более достоверна, чем при полном замораживании коэффициентов. Однако при сильном изменении параметров оба метода могут приводить к принципиальным ошибкам.
Таким образом, выявляется еще одна особенность нестационарных САУ: в них нельзя говорить об устойчивости в целом, а можно говорить лишь об устойчивости отдельных компонент вектора состояния или вектора выхода.
4.1.2. Особенности процессоввнелинейныхСАУ
Система автоматического управления называется нелинейной, если в ней содержится хотя бы один нелинейный элемент. Это приводит в общем случае или к системе нелинейных дифференциальных и алгебраических уравнений, или к единому нелинейному
дифференциальному уравнению САУ. |
|
|
|
На структурных схемах |
нелинейные элементы |
|
u = F (x ) изображаются в виде, как это представлено на |
|
Рисунок 1 - Схема |
рисунке 1, где x - входной, а u - выходной сигналы. |
|
нелинейного элемента |
Из-заналичия нелинейных элементов в нелинейных САУ |
|
|
||
проявляются свойства, которых нет в системах линейных.
Главное из них заключается в особой чувствительности нелинейных САУ к начальным условиям и внешним возмущениям. Проявляется это в наличии устойчивых периодических режимов - автоколебаний, а также во влиянии внешних возмущений на устойчивость нелинейной системы. Эти явления в линейных САУ отсутствуют как таковые.
Из-за особенностей нелинейных систем для их исследования было введено понятие так называемогофазового пространства. Обычно это пространство, координатами (фазами) которого являются регулируемая
величина x и ее производные до n − 1 -го порядка, где n - порядок САУ.
Чаще всего для исследования нелинейных систем используют частный случай фазового пространства - так называемую фазовую плоскость. Она представлена на рисунке 2, где в качестве оси абсцисс выступает регулируемая
величина x,авкачествеосиординатиспользуетсяеепроизводная x .
Если нелинейная САУ устойчива (неустойчива) вблизи начала координат фазового пространства, то говорят, что она устойчива (неустойчива) в “малом”. Если нелинейная САУ устойчива (неустойчива) вдали от начала координат, то говорят, что такая система устойчива (неустойчива) в “большом”. Оба эти состояния - и “большое”, и “малое” - разделяет
43
граничная поверхность,которая может характеризовать или границуобласти устойчивости по возмущениям, или автоколебательный процесс.
Поведение нелинейной САУ в фазовом пространстве отображается так называемой фазовой траекторией. Под ней понимают графическое изображение пути из любого начальногосостоянияСАУвлюбоееёконечноесостояние.Совокупностьфазовыхтраекторий
часто называют фазовым портретом. На рисунке 2 представлен фазовый |
|
|
|
портрет устойчивой в “малом” (из M |
1 - в ноль) и неустойчивой в “большом” (из M |
2 |
- в |
бесконечность)нелинейнойсистемы. |
|
|
|
4.1.3. Метод фазового пространства
Основу метода фазового пространства составляют все способы, позволяющие изобразить траекторию движения САУ из одного состояния в другое в соответствующем фазовом пространстве. Особенно наглядно представляется движение САУ на фазовой плоскости, если известны аналитические формулы для некоторых видов процессов.
Пусть САУ переходит из одного состояния в другое по экспоненте
Следовательно,
Рисунок 3 - Фазовые траектории
x |
= |
c e λ t , c = c o n s t , λ = c o n s t . |
(3) |
||||
x = |
c λ e λ t , e λ t |
= |
x |
, |
x = λ x . |
(4) |
|
|
|||||||
|
|
|
|
c |
|
|
|
|
На |
фазовой |
плоскости |
выражение |
x = λx |
||
представляет собой уравнение прямой, проходящей через начало координат. При отрицательной величине параметра
λ процесс (3) затухает со временем. Следовательно, стрелка на прямой направлена к началу координат
комплексной плоскости (см. рисунок 3). При |
|
||||
положительной величине λ |
прямая |
x |
= λ |
x |
уходит в |
|
|
||||
бесконечность, а стрелка направлена от начала координат
комплексной плоскости. На рис.3 представлены соответствующие траектории движения системы (3). При этом x 0 = λx 0 .
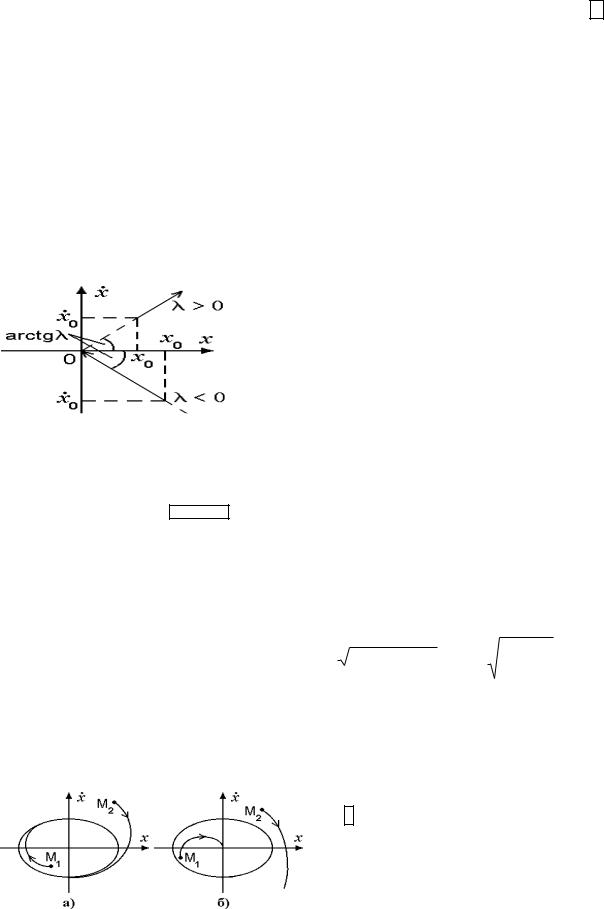
Найдём теперь траекторию движения характеристической точки на фазовой плоскости, если процесс имеет форму синусоиды
x = a sin ωt ,a = const ,ω = const . |
|
|
|
|
(5) |
||||||||
При этом для скорости процесса справедливо соотношение |
|
|
2 . |
|
(6) |
||||||||
x = a ω c o s ωt = a ω 1 − s in 2 ωt = a ω 1 − |
x |
|
|||||||||||
|
|
|
|
||||||||||
a 2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
После возведения в квадрат выражений (5),(6) и несложных преобразований (с учётом |
|||||||||||||
тождества sin 2 ωt + cos2 ωt = 1 ) можно получить выражение |
|
|
|
|
|
|
|||||||
|
x 2 |
+ |
|
x 2 = |
. |
|
|
|
|
|
(7) |
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
a 2 ω 2 |
|
a 2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Это |
уравнение |
эллипса с |
полуосями |
|||||
|
|
L1 |
= a ω |
и L2 = a . Как |
следствие, |
при |
|||||||
|
|
представлении синусоиды (5) на фазовой |
|||||||||||
|
|
плоскости |
будет |
наблюдаться |
движение |
||||||||
|
|
характеристической |
точки |
M {x ,x} |
по |
||||||||
Рисунок 4 - Варианты циклов: а) устойчивый; б) неустойчивый
44
эллипсу(7). Его же часто называют циклом. Циклы могут быть устойчивые и
неустойчивые. Если характеристическая точка
стремится удалиться от цикла (7), то его называют неустойчивым. Если эта точка стремится
