
- •В.Г. НОВИКОВ
- •ВВЕДЕНИЕ .................................................................
- •ТЕМА 5. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В
- •ВВЕДЕНИЕ
- •1.1. Введение
- •MatLab\ TOOLBOX\ CONTROL.
- •1.2. Ввод и преобразование моделей
- •sysd=c2d(sys, Ts, method).
- •2.1. Введение
- •h= freqs (b,a,w).
- •4.2. Моделирования процессов в линейных нестационарных и нелинейных динамических системах с использованием подсистемы MatLab SIMULINK
- •СПРАВКА
- •5. 1. Введение
- •5. 2. Пример имитационного моделирования процессов с использованием подсистемы MatLab SIMULINK
- •СПРАВКА
- •Использованные источники
7
Для многомерной системы (с несколькими входами и выходами) – массив ячеек из векторов-строк размером nY на nU.
Variable – Имя (тип)переменной.
Специфическиеатрибуты ZPK – объектов: z – Нули
Дляодномерной системы- вектор-строка;
Для многомерной системы – массив ячеек из векторов-строк размером nY на nU. p – Полюсы
Дляодномерной системы- вектор-строка;
Для многомерной системы – массив ячеек из векторов-строк размером nY на nU. k – Коэффициент передачи
Для одномерной системы - число;
Для многомерной системы – матрица размером nY на nU.
СпецифическиеатрибутыSS – объектов (моделейпространства состояний):
a, b, c, d – A, B, C, D – матрицы, в соответствии с уравнениями в переменных состояния:
x = Ax + Bu,
y = Cx + Du.
e - E – матрица для систем Descriptor’а (описателя). По умолчанию E= eye (size(A)). StateName – имя переменной состояния (не обязательное). Массив ячеек nX на 1из
строк.
Атрибуты, общиедлявсехLTI-моделей: Ts – Дискрет по времени (в секундах).
Ts = -1 для дискретных систем; Ts = 0 для непрерывных систем.
Td – Задержка входов (в секундах).
InputName – Имена входов.
Строка - для систем с одним входом.
Массив ячеек nX на 1из строк – для системы с несколькими входами.
OutpuName – Имена выходов.
Строка - для систем с одним входом.
Массив ячеек nX на 1из строк – для системы с несколькими входами.
Notes – Заметки.
Userdata – Дополнительнаяинформацияили данные.
1.2.Ввод и преобразование моделей
1.2.1.Основныеположения
Ввод модели линейной стационарной системы (ЛСС) в среду пакета CONTROL возможен в трех формах:
-в форме матриц пространства состояний;
-в виде коэффициентовчислителя и знаменателей передаточной функции;
-в форме задания нулей, полюсов и коэффициента передачи системы.
Кпроцедурам создания LTIмоделей относятся:
ss Создает модель пространства состояния по заданным матрицам A, B, C, D уравнений состояния системы.
8
dss Создает аналогичную модель по описанию пространства состояния более общего вида, когда уравнения переменных состояния не разрешены относительно производных.
tf Создает модель позаданным передаточным функциям системы.
zpk Создает модель по заданным нулям, полюсам и коэффициентам передачи системы.
filt Создает модель по дискретным передаточным функциям системы, записанным в форме полинома от z-1.
set Присваивает значения некоторым другим полям (атрибутам) LTIобъекта (названиям входов и выходов, названиям системы и т.п.).
get Выдает значения атрибутов объекта.
Указанные процедуры позволяют создавать как непрерывные модели, так и дискретные.
В последнем случае к числу входных параметров процедуры следует добавить в конце значения параметра Ts – шага дискретизации, а вводимые значения коэффициентов уже должны задавать параметры дискретных передаточных функций (для tf и zpk), либо матрицы конечно-разностных уравнений пространства состояний (при использовании процедур ss и dss).
При использовании процедуры filt должны задаваться векторы коэффициентов числителя и знаменателя дискретной передаточной функции, представленной в виде отношения полиномов от z-1.
Процедуры ss, dss, tf и zpk применяются также для преобразования моделей из одной из указанных форм в другую.
Модель, заданную как непрерывная, можно преобразовать в дискретную форму, воспользовавшись процедурой c2d в соответствии со схемой:
sysd=c2d(sys, Ts, method).
Здесь sys – исходная непрерывная заданная модель;
sysd – получаемый в результате работы процедуры дискретный аналог исходной системы;
Ts – задаваемое значение шага дискретизации;
method – параметр, определяющий методдискретизации.Например:
‘zoh’ – соответствует применению экстрополятора нулевого порядка: внутри интервала дискретизации сигналы аппроксимируются постоянной величиной, равной значению сигнала в начале интервала дискретизации;
‘foh’ - соответствует применению экстрополятора первого порядка: внутри интервала дискретизации сигналы аппроксимируются отрезками прямых, проходящих через концы кривой сигнала в интервале дискретизации.
Процедура d2c осуществляет обратную операцию – переводит дискретную систему в непрерывную.
Процедура d2d позволяет переопределить дискретную систему, меняя шаг дискретизации:
sys1=d2d(sys, Ts).
Для создания модели нужно предварительно либо перевести уравнения всей системы
кформе уравнений пространства состояния, либо найти передаточные функции системы.
Вобщем случае это довольно сложно.
9
Вто жевремя реальныеСАУ состоят из соединенных междусобой отдельныхблоков (динамических звеньев), уравнения которых достаточно просты.
Поэтому в практике проектирования САУ принято использовать структурные методы, когда САУ задается как определенная схема соединения отдельных элементарных динамических звеньев, и фактически проектируется одно или несколько из этих звеньев таким образом, чтобы обеспечить заданное качество всей системы.
В соответствии с этим в MatLab предусмотрена возможность “набирать” программно схему САУ путем:
-предварительноговводамоделей звеньев,составляющих САУ,и
-последующего “соединения”этих звеньеввединую структуру.
Кпроцедурам, осуществляющим расчет характеристик соединений отдельных звеньев, относятся:
plus (minus)– выполняет параллельное соединении указанных звеньев;
parallel - выполняет ту же процедуру, параллельного соединения звеньев; отличие
– может использоваться для многомерных систем и для осуществления параллельного соединения лишь по некоторым входам и выходам
mtimes (или знак “*” между именами звеньев) – выполняет последовательное соединении указанных звеньев; применяется для одномерных систем;
series - выполняет последовательное частичное соединении многомерных систем; feedback - выполняет такое соединении двух звеньев, когда второе указанное звено
составляет цепь отрицательной обратной связи для первого звена;
append - выполняет формальное объединение не связанных между собой систем (добавление выходов и входов второй системы к выходам и входам первой);
connect – установление соединений входов и выходов многомерной системы, созданной формальным объединением процедурой append;
inv – рассчитывает САУ, обратную указанной, т.е. такую, у которой выходы и входы поменяли местами.
1.2.2. Примерсозданиямодели
Создать модель движения системы (торпеды) в горизонтальном канале, состоящую из подмодели углового движения вокруг вертикальной оси и из подмодели цепи управления.
При этом подмодель углового движения может быть представлена в виде двух последовательно соединенных звеньев:
- апериодического
W1 = |
25 |
и |
||
100s +50 |
||||
|
|
|||
- интегрирующего |
||||
W = |
1 . |
|
||
2 |
s |
|
|
|
|
|
|||
В свою очередь подмодель цепи управления может быть представлена в виде двух параллельно соединенных частей:
– части, управляемой гироскопом направления и представляющей собой обычное
усилительное звено K; |
|
- части, управляемой гиротахометром, которую можно представить |
как |
дифференцирующе-колебательное звено W3. |
|
Соответствующая структурная схемаимеет вид,представленный нарисунке, |
|

|
|
|
10 |
|
|
Mв |
|
|
|
|
ψ |
– |
W1 |
|
W2 |
||
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Mу
W3
где M – момент внешних сил относительно вертикали; ω - угловая скорость торпеды;
ψ – угол поворота торпеды вокруг вертикали (угол рыскания).
Mу– момент управляющих сил, создаваемый при помощи рулей управления.
Решение.
Подмодель угловогодвижения:
>> W1=tf(25,[100 50]) Transfer function:
25
100 s + 50
>> W2=tf(1, [1 0]) Transfer function: 1
---.
s
Последовательноесоединениеэтих звеньевможноосуществить двумя способами:
– применениемпроцедурыseries:
>> W0=series(W1, W2) Transfer function:
25
;
100 s^2 + 50 s
- либо просто операцией “перемножения” моделей:
>> W01=W1*W2 Transfer function:
25
.
100 s^2 + 50 s
Теперь сформируем цепь управления, входом которой является угол рыскания торпеды ψ, а выходом – момент Mу, накладываемый на торпеду со стороны ее рулей направления.
Усилительное звено:
>> K=tf(2,1) Transfer function: 2
Дифференцирующе-колебательное звено W3:
>> W3=tf([100 0], [1 10 100]) Transfer function:
100 s
.
s^2 + 10 s + 100

11
Параллельное соединение этих двух звеньев управления можно осуществить тоже двумя способами:
- либо используя процедуруparallel
>> U1=parallel(K,W3) Transfer function:
2 s^2 + 120 s + 200
s^2 + 10 s + 100
- либо применяя операцию “сложения” моделей
>> U=K+W3 Transfer function: 2 s^2 + 120 s + 200
.
s^2 + 10 s + 100
Теперь найдем модель всей САУ угловым движением торпеды, рассматривая цепь управления как цепь отрицательной обратной связи для торпеды, пользуясь для объединения прямой и обратной цепи процедурой feedback:
>> sys=feedback(W01,U) Transfer function:
25 s^2 + 250 s + 2500
.
100 s^4 + 1050 s^3 + 10550 s^2 + 8000 s + 5000
После того, как система сформирована, можно ввести при помощи процедуры set некоторые ее символьные описания. В частности присвоить названия входам и выходам системы, а также дать краткий комментарий к самой системе.
>>set(sys,'InputName','Моментсил','OutputName','Уголрыскания')
>>set(sys,'Notes','Угловое движениеторпеды')
>>get(sys)
num: {[0 0 25 250 2.5e+003]}
den: {[100 1.05e+003 1.06e+004 8e+003 5e+003]} Variable: 's'
Ts: 0 ioDelay: 0 InputDelay: 0 OutputDelay: 0
InputName: {'Момент сил'}
OutputName: {'Угол рыскания'}
InputGroup: [1x1 struct] OutputGroup: [1x1 struct]
Notes: {'Угловое движениеторпеды'}
UserData: []
1.3.Анализсистемы
1.3.1.Общиеположения
Пакет CONTROL предоставляет пакет процедур для осуществления анализа САУ, прежде всего, для определения отклика системы на внешние воздействия как во временной, так и в частотной областях.
1.3.1.1. Примеры анализа во временной области
Для нахождения временных откликов системы на внешние воздействия некоторых видов предусмотрены функции:
impulse Нахождение отклика на импульсное входное воздействие.
step Нахождение реакции системы на единичный скачок входного воздействия.
12
initial Определение собственного движения системы при произвольных начальных условиях.
lsim Определение реакции системы на входное воздействие произвольной формы, задаваемое в виде вектора его значений во времени.
1.3.1.2. Примеры анализа в частотной области
Группа процедур для представления реакции системы на гармонические воздействия в частотной области:
bode Строит график АЧХ и ФЧХ (диаграммуБоде) указанной системы.
nyquist Строит в комплексной плоскости график АФХ разомкнутой системы в полярных декартовых координатах.
nichols Строит карту Николса системы, т.е. график АФХ разомкнутой системы в декартовых координатах.
sigma Строит график зависимости от частоты сингулярных значений системы; обычно совпадает с АЧХ системы.
margin Строит диаграммуБоде с указанием запасов по амплитуде и по фазе.
1.3.1.3. Процедуры, вычисляющие отдельные характеристики и графически показывающие расположение полюсов и нулей системы
pole Расчет полюсов системы.
zpkdata Расчет полюсов, нулей и коэффициента передачи системы.
pzmap Построение на комплексной плоскости карты расположения нулей и полюсов системы.
1.3.2. Примеры анализаво временной области
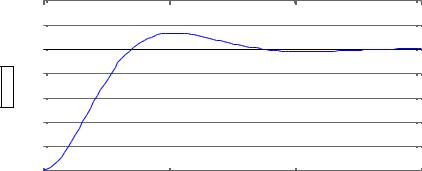
Применяя процедуруstep к созданной в п. 2.2модели,
>> step(sys)
можно получить график
Amplitude
Step Response
From: Момент сил To: Угол рыскания
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0 0 |
5 |
10 |
15 |
Time (sec)
Аналогично, использование процедуры impulse
>> impulse(sys)
приведет к появлению в графическом окне графика, приведенного ниже:
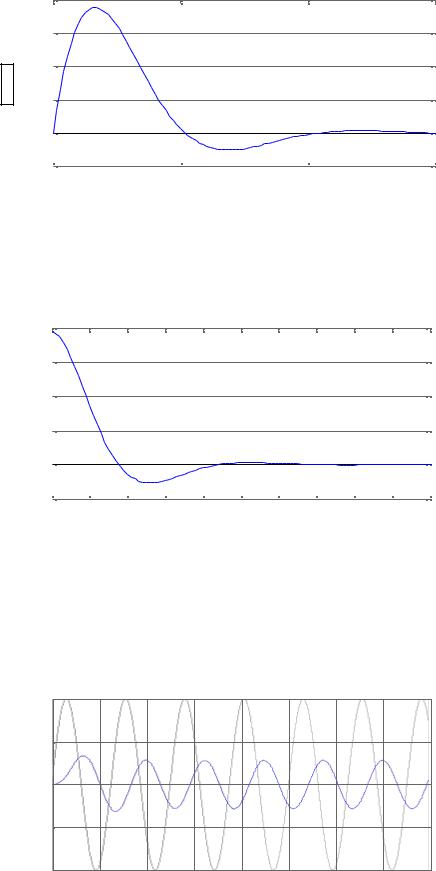
13
Amplitude
Impulse Response
From: Момент сил To: Угол рыскания
0.2
0.15
0.1
0.05
0 |
|
|
|
|
-0.05 |
0 |
5 |
10 |
15 |
Time (sec)
При применении процедуры initial необходимо в число входных параметров включить, во-первых, полный вектор всех начальных условий по переменным состояния, а, во-вторых, момент времени окончания процесса интегрирования.
>>sssys=ss(sys)
>>initial(sssys,[0 0 0 1],20)
Получим
Amplitude |
To:Уголрыскания |
Response to Initial Conditions
0.4
0.3
0.2
0.1
0 |
|
|
|
|
|
|
|
|
|
|
-0.10 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
|
|
|
|
Time (sec) |
|
|
|
|
|
Для применения процедуры lsim необходимо предварительно задать вектор t значений времени, в которых будут заданы значения входного воздействия, а затем задать вектор u значений входной величины в указанные моменты времени
>> t=0:0.01:40; u=sin(t); lsim(sssys,u,t);grid
Результат представлен на следующей фигуре:
Amplitude |
To: Уголрыскания |
Linear Simulation Results
1
0.5
0
-0.5
-10 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
|
|
|
|
Time (sec) |
|
|
|
|

14
1.3.3. Примеры анализавчастотной области
>> bode(sys)
Magnitude(dB)
Bode Diagram
From: Момент сил To: Угол рыскания
0
-20
-40
-60
-80
-100 0
Phase(deg) |
-90 |
|
|
|
|
|
-180 |
-2 |
|
10 |
|
>> nyquist(sys)
1 |
|
0.8 |
4 dB 2 dB |
|
0.66 dB
|
0.4 10 dB |
|
|
|
|
AyraingaImxsi |
0.2 |
20 dB |
|
||
|
|
|
|
0 |
|
|
-0.2 |
|
|
|
|
|
-0.4 |
|
|
-0.6 |
|
|
-0.8 |
|
|
-1 |
|
|
-1 |
|
>> nichols(sys)
|
0 |
|
-10 |
|
-20 |
apG-LneOpoin(dB) |
-30 |
|
|
|
-40 |
|
-50 |
|
-60 |
|
-70 |
|
-180 |
>> sigma(sys)
|
0 |
|
-10 |
|
-20 |
|
-30 |
eluarVlaugSins(dB) |
-40 |
|
|
|
-50 |
|
-60 |
|
-70 |
|
-80 |
|
-90 |
|
-100 |
|
10- 2 |
>> margin(sys);grid
10-1 |
100 |
101 |
102 |
|
Frequency (rad/sec) |
|
|
|
Nyquist Diagram |
|
|
From: Момент сил To: Угол рыскания |
|
|
|
0 dB |
-2 dB |
|
-4 dB |
|
|
|
-6 dB |
-10 dB -20 dB
-0.5 |
0 |
0.5 |
|
Real Axis |
|
Nichols Chart
From: Момент сил To: Угол рыскания
-135 |
-90 |
-45 |
0 |
|
Open-Loop Phase (deg) |
|
|
Singular Values
10- 1 |
100 |
101 |
102 |
|
Frequency (rad/sec) |
|
|

15
 Phase(deg) Magnitude(dB)
Phase(deg) Magnitude(dB)
Bode Diagram
Gm = Inf dB (at Inf rad/sec) , Pm = Inf
From: Момент сил To: Угол рыскания
0 -20 -40 -60 -80
-100 0
-45 -90 -135
-180 |
10- 1 |
100 |
101 |
102 |
10- 2 |
Frequency (rad/sec)
1.3.4. Примеры примененияпроцедур длявычисления полюсов и нулей системы
>> pole(sys) ans =
-4.8653 + 8.5924i -4.8653 - 8.5924i -0.3847 + 0.6040i -0.3847 - 0.6040i
>> sysz=zpk(sys)
Zero/pole/gain from input "Момент сил" to output "Угол рыскания": 0.25 (s^2 + 10s + 100)
(s^2 + 0.7693s + 0.5128) (s^2 + 9.731s + 97.5)
>> [z,p,k]=zpkdata(sysz,'v') z =
-5.0000 + 8.6603i -5.0000 - 8.6603i
p =
-4.8653 + 8.5924i -4.8653 - 8.5924i -0.3847 + 0.6040i -0.3847 - 0.6040i
k=
0.2500
>>pzmap(sys); grid
Результат представлен нарисункениже
ImaginaryAxis
10 |
|
|
|
Pole-Zero Map |
|
|
|
|
||
|
0.4 |
|
0.28 |
|
0.2 |
0.14 |
0.09 |
0.04 |
|
|
8 |
|
|
|
8 |
||||||
|
|
|
|
|
|
|
|
|
||
0.56 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
0.8 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
-4 |
0.8 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
-6 |
|
|
|
|
|
|
|
|
|
6 |
|
0.56 |
|
|
|
|
|
|
|
|
|
-8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
0.4 |
|
0.28 |
|
0.2 |
0.14 |
0.09 |
0.04 |
|
-10 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
-5 |
-4.5 |
-4 |
-3.5 |
-3 |
-2.5 |
-2 |
-1.5 |
-1 |
-0.5 |
0 |
|
|
|
|
Real Axis |
|
|
|
|
|
|
1.4.Заданиенасамостоятельнуюработу
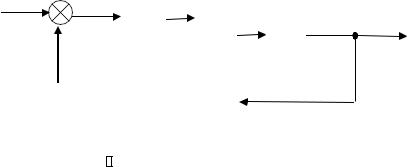
1.4.1.Структурнаясхемамодели
Создать модель системы слежения, представленнойнарисунке:
16
|
|
|
εвх |
|
|
|
|
|
|
|
U1 |
|
|
|
U2 |
|
|
|
εвых |
|||
|
|
|
|
|
|
|
|
W1 |
|
|
|
|
|
|
||||||||
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
W2 |
|
|
|
|
|
W3 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Kос |
|
|
|
|
|
|
|
На рисунке: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
W = |
K пр (T1 s +1 ) |
; |
W |
|
|
|
|
(T s + 1 ) |
; W |
= |
. |
|
||||||||||
|
|
|
|
2 |
= |
|
3 |
|
|
|
|
|
|
|||||||||
|
T2 s + 1 |
|
s(T4 s + 1 ) |
|
|
|
s |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.4.2. Требованияк исследованию модели
Провести исследованиесистемы, при этом:
-оценить временныеотклики системы;
-определить реакциюсистемына гармоническиевоздействия;
-определить полюса и нули системы.
Представитьсоответствующиеграфики.
Критерием при исследовании должны служить устойчивость системы и показатели качества.
В случае неудовлетворительного качества системы при исходных параметрах (см. таблицувариантов)выбрать требуемыепараметрыкорректирующего фильтраW1(s) T1, T2, Kпр.
1.4.3. Исходныепараметрымодели
Исходные параметры заданной системы для каждого варианта заданы в таблице:
№ |
T1, c |
T2, c |
T3, c |
T4, c |
Kпр |
Kос |
|
варианта |
|||||||
|
|
|
|
|
|
||
1 |
0.40 |
0.020 |
0.050 |
0.0045 |
15.0 |
1.0 |
|
2 |
0.10 |
0.030 |
0.050 |
0.0045 |
10.0 |
1.0 |
|
3 |
0.20 |
0.040 |
0.050 |
0.0045 |
9.0 |
1.0 |
|
4 |
0.30 |
0.050 |
0.050 |
0.0045 |
15.0 |
1.0 |
|
5 |
0.40 |
0.055 |
0.030 |
0.0050 |
10.0 |
1.0 |
|
6 |
0.50 |
0.065 |
0.050 |
0.0045 |
9.0 |
1.0 |
|
7 |
0.60 |
0.065 |
0.050 |
0.0045 |
12.0 |
1.0 |
|
8 |
0.70 |
0.065 |
0.050 |
0.0045 |
11.0 |
1.0 |
|
9 |
0.80 |
0.085 |
0.050 |
0.0045 |
10.0 |
2.0 |
|
10 |
0.90 |
0.095 |
0.030 |
0.0050 |
9.0 |
2.0 |
|
11 |
1.00 |
0.095 |
0.040 |
0.0020 |
8.0 |
2.0 |
|
12 |
1.11 |
0.095 |
0.040 |
0.0030 |
7.0 |
2.0 |
|
13 |
1.00 |
0.100 |
0.040 |
0.0020 |
6.0 |
2.0 |
|
14 |
0.90 |
0.100 |
0.040 |
0.0030 |
5.0 |
2.0 |
|
15 |
0.80 |
0.100 |
0.050 |
0.0025 |
5.0 |
2.0 |
|
16 |
0.80 |
0.100 |
0.050 |
0.0025 |
6.0 |
2.0 |
|
17 |
0.50 |
0.050 |
0.040 |
0.0050 |
6.0 |
2.0 |
|
18 |
0.60 |
0.060 |
0.060 |
0.0040 |
7.0 |
2.0 |
|
19 |
0.40 |
0.045 |
0.050 |
0.0045 |
8.0 |
1.5 |
|
20 |
0.70 |
0.065 |
0.050 |
0.0045 |
8.0 |
1.0 |
17
1.4.4. Отчетностьполабораторнойработе
Результаты исследований для отчета оформить в текстовом процессоре Word в соответствии с требованиями ГОСТ к оформлению научно-технической документации.
