ТЕХНОЛОГИИ

ПРОГРАММИРОВАНИЯ

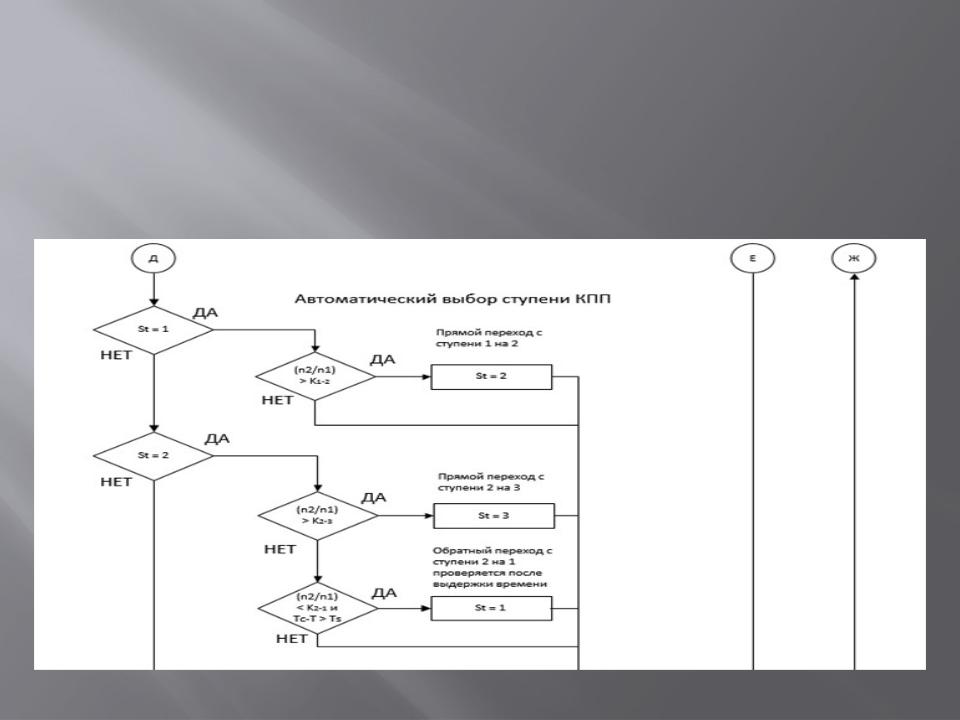
Управляющий граф

Блок схема автоматического переключения КПП

Типы вершин

Функциональнаявершина − имеет один вход и один выход

Предикатная вершина – имеет один вход и два выхода. Функция Р передаёт управление по одной из ветвей в зависимости от значения функции Р, которое может принимать значения true (истина) и false (ложь).

Объединяющая вершина (вершина «слияния») – обеспечивает передачу управления от одного из двух входов к выходу.

Метрика (мера сложности) Холстеда

NUOprtr (Number of Unique Operators) — число уникальных операторов программы, включая символы-разделители, имена процедур и знаки операций (словарь операторов);

NUOprnd (Number of Unique Operands) — число уникальных операндов программы (словарь операндов);

Noprtr (Number of Operators) — общее число операторов в программе;

Noprnd (Number of Operands) — общее число операндов в программе.

Метрики сложности потока управления программы

1 Цикломатическая сложность(метод Мак-Кейба)

V(G)=e — n + 2p, где e — количество дуг, n — количество вершин, p — число компонент связности

2 Цикломатическая сложность(метод Хансена) учет количества операторов

3 метрики Харрисона, Мейджела (учитывают сложность и протяженность)

Функциональная мера программы

Функциональная мера программы — это сумма приведенных сложностей всех вершин управляющего графа

Функциональным отношением называется отношение числа вершин в управляющем графе к его функциональной сложности, причем из числа вершин исключаются терминальные.

Метрика Пивоварского N(G) = v *(G) + СУММАPi

Мера Вудворда

Метрики сложности потока управления данными

Метрика Чепина: все множество переменных, составляющих список ввода-вывода, разбивается на 4 функциональные группы :

1.P — вводимые переменные для расчетов и для обеспечения вывода,

2.M — модифицируемые, или создаваемые внутри программы переменные,

3.C — переменные, участвующие в управлении работой программного модуля (управляющие переменные),

4.T — не используемые в программе («паразитные») переменные.

Числовое вычисление метрики

Q = a1*P + a2*M + a3*C + a4*T,

где a1, a2, a3, a4 — весовые коэффициенты

Объектно-ориентированные метрики

Метрика Мартина

1. Ca: Центростремительное сцепление. Количество классов вне этой категории, которые зависят от классов внутри этой категории.

2.Ce: Центробежное сцепление. Количество классов внутри этой категории, которые зависят от классов вне этой категории.

3.I: Нестабильность: I = Ce / (Ca+Ce). Эта метрика имеет диапазон значений [0,1].

I = 0 указывает максимально стабильную категорию.

I = 1 указывает максимально не стабильную категорию.

Можно определять метрику, которая измеряет абстрактность (если категория абстрактна, то она достаточно гибкая и может быть легко расширена) категории следующим образом:

A: Абстрактность: A = nA / nAll.

nA — количество_абстрактных_классов_в_категории. nAll — oбщее_количество_классов_в_категории. Значения этой метрики меняются в диапазоне [0,1]. 0 = категория полностью конкретна, 1 = категория полностью абстрактна.