TAU-Lekcii

уравнению (10.59), так и системы определения погрешности X по уравнению (10.60). Требуется, чтобы погрешность наблюдения X(t) быстро затухала во времени.

Существуют и другие схемы наблюдателей, каждый из которых обладает своими особенностями.

10.7. Прямой корневой метод синтеза систем управления

Качество процесса управления, как отмечалось в разделе 6.5, определяется расположением корней характеристического уравнения замкнутой системы. В связи с этим разработаны различные корневые методы расчета систем управления. Одним из них является прямой корневой метод синтеза, называемый модальным методом синтеза системы по заданному качеству процесса управления [2]. Вводится целевая функция, которая является функциональным выражением поставленной цели при синтезе системы. Обычно целевую функцию представляют как ограниченную скалярную действительную непрерывно дифференцируемую функцию F = F(q1, q2, ..., qn) искомых параметров qi (i = 1, 2, ..., n) регулятора системы.

При этом общую задачу рассматривают как выбор вектора параметров q = [q1, q2, ..., qn]T , оптимизирующего в допустимых пределах значение целевой функции на допустимом множестве Qn.

Однако часто при проектировании системы не проводят подобную оптимизацию, а исходят из удовлетворения заданным требованиям.

В этом случае задача синтеза состоит в том, чтобы, опираясь на ряд качественных показателей системы, найти соответствующее расположение корней характеристического уравнения замкнутой системы 1, 2, ..., n на комплексной плоскости, а затем найти параметры регулятора, обеспечивающие заданное расположение указанных корней. При этом исходными качественными показателями могут быть, например, вид переходного процесса, время регулирования, колеба-

191

тельность, интегральная квадратичная ошибка и так далее. Указанные требования на одновременное выполнение различных качественных показателей создаваемой системы приводят к задаче выделения на комплексной плоскости соответствующих областей допустимого расположения корней характеристического уравнения замкнутой системы.

Характеристическое уравнение системы D( ) = 0 (10.26) переписывается в виде

Каждый коэффициент ai (i = 1, 2, ..., n) является функцией от параметров объекта управления и регулятора, то есть

где q = [q1, q2, ..., qn]T - искомый параметрический вектор.

Для решения задачи модального синтеза ставится в соответствии с (10.61) и (10.62) желаемый характеристический многочлен

D*( ) = ( 1* ) ( 2* ) ... ( n* );

после раскрытия скобок получаем

где i* - желаемые значения корней характеристического полинома, лежащие в заданных пределах:

Приравнивая соответствующие коэффициенты (10.62) и (10.64),

192

получаем

Таким образом, имеем систему n уравнений с n неизвестными, решая которую непосредственно или численными методами, можно определить все n значений параметров вектора q = [q1, q2, ..., qn]T.

Очевидно, что независимое назначение всех коэффициентов характеристического уравнения ai (i = 1, 2, ..., n) возможно лишь при числе корректирующих параметров не менее n. Это обстоятельство делает возможным предписанное назначение желаемых корней i (i = 1, 2, ..., n).

В настоящее время для синтеза систем имеются разнообразные программные средства. Примером может служить CLASSiC (Complex Linear Analysis and Structure Synthesis in Control) - программа для пер-

сональных компьютеров класса IBM PC, позволяющая строить математические модели, анализировать и синтезировать системы управления со сложной структурой [16].

ВОПРОСЫ К РАЗДЕЛУ 10

1.Что такое состояние, пространство состояний, вектор состояния?

2.Запишите стандартную форму уравнений в простран-

стве

состояний. Поясните физический смысл уравнений.

3.Как получить сопровождающую матрицу или матрицу Фробениуса?

4.От каких параметров передаточной функции зависят элементы матрицы системы управления?

5.Перечислите свойства матричной экспоненты.

6.Какова структура решения уравнений переменных

состояния?

193

7. Перечислите характеристики систем в пространстве состояний. Дайте понятие управляемости и наблюдаемо-

сти

систем и критерии их проверки.

8. Запишите характеристический определитель матрицы

A.

9.Что представляет собой нормальная форма уравнений в пространстве состояний? Как ее получить?

10.Дайте понятие управления по состоянию. Расскажите

о

системах управления состоянием. Что представляет

собой

модальный регулятор?

11.Каким образом можно оценить координаты состояния систем?

12.Поясните постановку задачи модального метода син-

теза

систем по заданному качеству процесса управления.

194

БИБЛИОГРАФИЧЕСКИЙ СПИСОК К МОДУЛЮ 1

1.Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. - М.: Наука, 1975. - 768с.

2.Попов Е.П. Теория линейных систем автоматического регулирования и управления. - М.: Наука, 1989. - 304с.

3.Попов Е.П. Теория нелинейных систем автоматического регулирования и управления. - М.: Наука, 1979. - 256с.

4.Первозванский А.А. Курс теории автоматического управ-

ления. - М.: Наука, 1986. - 616с.

5.Воронов А.А. Основы теории автоматического управления. Особые линейные и нелинейные системы. - М.: Энергоиздат,

1981. - 304 с.

6.Коновалов Г.Ф. Радиоавтоматика. - М.: Высшая школа,

1990. - 335с.

7.Топчеев Ю.И. Атлас для проектирования систем автоматического регулирования. - М.: Машиностроение, 1989. - 752 с.

8.Куропаткин П.В. Теория автоматического управления. - М.: Высшая школа, 1973. - 507 с.

9.Теория управления. Терминология / Под ред. Б.Г.Волика. -

М.: Наука, 1988. - 56 с.

10.Расчет автоматических систем / Под ред. А.В.Фатеева. - М.: Высшая школа, 1973. - 336 с.

11.Сборник задач по теории автоматического регулирования и управления / Под ред. В.А.Бесекерского. - М.: Наука, 1978. - 512 с.

12.Иващенко Н.Н. Автоматическое регулирование. М.: Машиностроение, 1978. - 609 с.

13.Юревич Е.И. Теория автоматического управления. - Л.: Машиностроение, 1980. - 412 с.

14.Дидук Г.А. Методы теории матриц и их применение для исследования и проектирования систем управления. - Л.: СЗПИ,

1986. - 83 с.

195

15.Мирошник И.В., Болтунов Г.И. Системы и устройства управления технологическим оборудованием. - Л., 1990. - 38 с.

16.Имаев Д.Х. и др. Анализ и синтез систем управления. Теория. Методы. Примеры решения типовых задач с использованием персонального компьютера. - Санкт-Петербург, Гданьск, Сургут,

Томск, 1998. - 172 с.

196

Модуль 2

НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

2.1. Общие понятия и особенности нелинейных систем

Строго говоря, линейных систем в природе не существует, так как характеристики реальных устройств нелинейные и некоторые из них не могут быть линеаризованы, например, характеристика логического элемента. Кроме того, есть системы, например, релейные, адаптивные, в которых принципиально необходимо учитывать нелинейности.

Нелинейной системой называется такая система, в состав которой входит хотя бы одно звено, описываемое нелинейным уравнением. Такое звено называется нелинейным звеном или нелинейным элементом.

Уравнение является нелинейным, если некоторые координаты или их производные по времени входят в уравнение в виде произведений или степени, отличной от первой, а также если коэффициенты уравнения являются функциями некоторых координат или их производных.

При составлении дифференциальных уравнений нелинейных систем сначала составляют дифференциальные уравнения для каждого устройства системы. При этом характеристики устройств, допускающих линеаризацию, линеаризуются. В результате получают систему дифференциальных уравнений, в которой одно или несколько уравнений нелинейные. Устройства, допускающие линеаризацию, образуют линейную часть системы, а устройства, которые не могут быть линеаризованы, составляют нелинейную часть.

Путем эквивалентного преобразования структурных схем и нелинейных звеньев большое число нелинейных систем можно представить в виде замкнутого контура с последовательным включением не-

197

линейного элемента (НЭ) и линейной части (ЛЧ), как показано на рис.

2.1.

Рис. 2.1. Функциональная схема нелинейной системы: НЭ - нелинейный элемент; ЛЧ - линейная часть

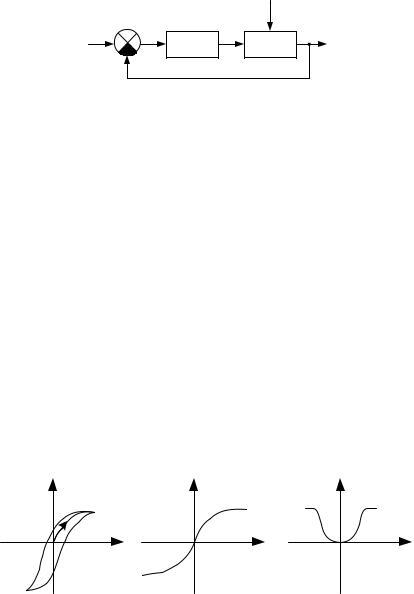
Классификация нелинейных элементов и систем. Нелинейные звенья классифицируются по различным признакам. Наибольшее распространение получила классификация по статическим и динамическим характеристикам, так как в системах чаще всего нелинейности приходится учитывать в виде характеристик. Эти характеристики могут быть как однозначными, так и двузначными (петлевыми), симметричными и несимметричными относительно начала координат.

Различают следующие основные типы нелинейных звеньев.

Нелинейные звенья с гладкими криволинейными характеристи-

ками. Примеры таких характеристик приведены на рис. 2.2.

Рис. 2.2. Гладкие криволинейные характеристики: а - гистерезисная; б, в - усилительные

На рис. 2.2,а изображена двузначная гистерезисная (запаздывающая) характеристика. Характеристика (рис. 2.2,б) отображает насыщение или ограничение и соответствует реальному амплитудному усилителю, а характеристика (рис. 2.2,в) - реальному усилителю

198

мощности. Характеристики (рис. 2.2,а и б) нечетно-симметричные, а характеристика (рис. 2.2,в) четно-симметричная.

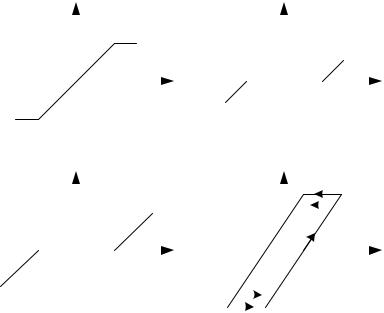
Нелинейные звенья с кусочно-линейными характеристиками.

Некоторые из таких характеристик представлены на рис. 2.3.

Рис. 2.3. Кусочно-линейные характеристики:

а- с насыщением; б - с зоной нечувствительности;

в- с насыщением и зоной нечувствительности; г - люфт

Характеристика (рис. 2.3,а) отображает насыщение, характеристика (рис. 2.3,б) зону нечувствительности, а характеристика (рис. 2.3,в) соответствует звену, обладающему одновременно зоной нечувствительности и насыщением. Характеристика (рис. 2.3,г) позволяет учесть люфт или зазор кинематической передачи.

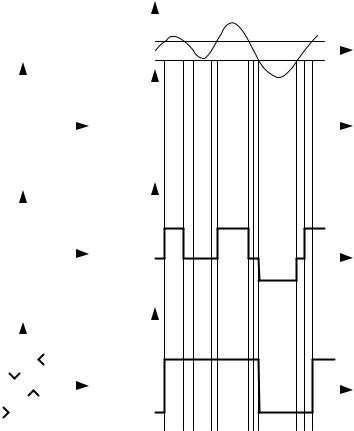
Релейные звенья это элементы, которые на своем выходе выдают конечное число фиксированных значений. Три наиболее типовые релейные характеристики изображены на рис. 2.4.

199

Рис. 2.4. Релейные характеристики:

а - идеальная; б - с зоной нечувствительности; в - гистерезисная

Характеристика (рис. 2.4,а) соответствует идеальному двухпозиционному реле, характеристика (рис. 2.3,б) трехпозиционному реле с зоной нечувствительности, а характеристика (рис. 2.3,в) двухпозиционному поляризованному реле.

Кроме того, на рис. 2.4 показано прохождение непрерывного сигнала через соответствующие типы реле. Откуда следует, что коэффициент передачи реле зависит от величины входного воздействия.

Для улучшения динамических свойств систем специально созданы нелинейные звенья с опережающими двузначными статическими характеристиками.

Часто встречаются элементы с несимметричными относительно начала координат статическими характеристиками.

200