3. Выполнение лабораторной работы

3.1 Получение выборки с генератора

В начале перед работой с аппаратурой PXI-1033 и NIElvis«прогрели» их в течение 15 минут для достижения нормальной рабочей температуры. Затем собрали схему, представленную ниже (рис.2).

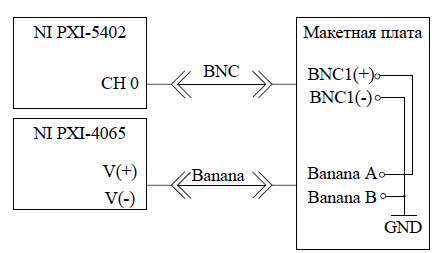
Рисунок 1: Схема получения выборки с генератора

Чтобы получить необходимые данные, запустили пакетные файлы blackbox.bat и collect_data.bat, которые исполнялись в течение не менее 3-х минут. После чего остановили процесс и переименовали созданный файл в data_x(n).txt.

Повторили данные действия дважды и получили две выборки в виде файлов data_x1.txt и data_x2.txt.

3.2 Получение выборки с источника напряжения

Собрали схему с источником напряжения для получения 3-ей выборки (рис.3).

Рисунок 2: Схема получения выборки с источника напряжения

Аналогично повторили действия с созданием нового файла и переименовали его в data_x3.txt– с выборкой №3.

3.3 Получение выборки без источника напряжения

Для получения 4-ой выборки собрали схему без источника напряжения (рис.4).

Рисунок 3: Схема получения выборки без источника напряжения

Аналогично повторили действия с созданием нового файла и переименовали его data_k4.txt– выборкой №4.

3.4 Обработка выборок с помощью Python 3.x

3.4.1 Расчёт параметров выборок

С помощью скрипта «calculatesampleparams.py» рассчитываем следующие параметры выборок:

• среднее арифметическое выборки - Mean;

• минимальное значение в выборке – Minimum value;

• максимальное значение в выборке – Maximum value;

• выборочное среднеквадратическое отклонение - Standard deviation;

• число элементов в выборке - Number ofelements;

• выборочное медианное значение - Median;

• выборочная дисперсия - Variance;

• выборочный коэффициент эксцесса – Kurtosis;

• выборочный коэффициент асимметрии – skew.

Внесём полученные значения в протокол измерений для каждой выборки (Таблицы 1-4):

Таблица 1 – Протокол измерений 1-ой выборки

Параметр	Значение
Номер выборки	1
Среднее арифметическое выборки	3,822251
Выборочная дисперсия	3,860972*
Минимальное значение в выборке	3,821617
Максимальное значение в выборке	3,823870
Выборочное среднеквадратическое отклонение	1,964936*
Число элементов в выборке	3340
Выборочное медианное значение	3,822224
Выборочный эксцесс	6,287150
Выборочный коэффициент асимметрии	1,432396

Таблица 2 – Протокол измерений 2-ой выборки

Параметр	Значение
Номер выборки	2
Среднее арифметическое выборки	-1,432168
Выборочная дисперсия	2,029466*
Минимальное значение в выборке	-1,432972
Максимальное значение в выборке	-1,431450
Выборочное среднеквадратическое отклонение	1,424593*
Число элементов в выборке	2123
Выборочное медианное значение	-1,432159
Выборочный эксцесс	2,310394
Выборочный коэффициент асимметрии	-6,522644*

Таблица 3 – Протокол измерений 3-ой выборки

Параметр	Значение
Номер выборки	3
Среднее арифметическое выборки	1,677185
Выборочная дисперсия	9,534293*
Минимальное значение в выборке	1,676861
Максимальное значение в выборке	1,677307
Выборочное среднеквадратическое отклонение	9,764370*
Число элементов в выборке	2297
Выборочное медианное значение	1,677224
Выборочный эксцесс	7,427525*
Выборочный коэффициент асимметрии	-1,298689

Таблица 4 – Протокол измерений 4-ой выборки

Параметр	Значение
Номер выборки	4
Среднее арифметическое выборки	-2,697839
Выборочная дисперсия	1,082688*
Минимальное значение в выборке	-3,771306*
Максимальное значение в выборке	3,284649*
Выборочное среднеквадратическое отклонение	1,040523*
Число элементов в выборке	3409
Выборочное медианное значение	-2,433283
Выборочный эксцесс	-1,379058*
Выборочный коэффициент асимметрии	-4,581844*