
Санкт-Петербургский
государственный электротехнический
университет “ЛЭТИ” им. В. И. Ульянова
(Ленина) (СПбГЭТУ «ЛЭТИ»)


Минобрнауки россии
Федеральное государственное автономное образовательное учреждение высшего образования

Кафедра теоретических основ электротехники
Отчет
по лабораторной работе № 9
по дисциплине «ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ»
Тема: «Исследование индуктивно-связанных цепей»
Вариант 23
Студент гр. 2305 |
|
|
Преподаватель |
|
Езеров К.С. |
Санкт-Петербург
2024 г.
Цель работы.
Экспериментальное определение параметров двух индуктивно-связанных катушек, проверка основных соотношений индуктивно-связанных цепей при различных соединениях катушек, а также исследование их в трансформаторном режиме работы.
Основные теоретические положения.
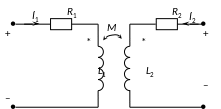 Схема
замещения двух индуктивно-связанных
катушек, удовлетворительно учитывающая
электромагнитные процессы в диапазоне
низких и средних частот, представлена
на рис. 9.1, где
Схема
замещения двух индуктивно-связанных
катушек, удовлетворительно учитывающая
электромагнитные процессы в диапазоне
низких и средних частот, представлена
на рис. 9.1, где
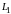 ,
,
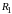 и
и
 ,
,
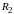 – индуктивности и сопротивления
соответственно первой и второй катушек;
– индуктивности и сопротивления
соответственно первой и второй катушек;
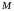 – взаимная индуктивность катушек.
– взаимная индуктивность катушек.
Рис. 9.1
Степень магнитной связи двух катушек определяется коэффициентом связи:
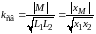 ,
(9.1)
,
(9.1)
где
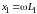 ,
,
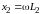 – индуктивные сопротивления катушек;
– индуктивные сопротивления катушек;
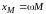 – сопротивление взаимной индуктивности,
при этом 0
– сопротивление взаимной индуктивности,
при этом 0
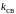 1.
1.
В режиме гармонических колебаний уравнения цепи, изображенной на рис. 9.1, имеют вид:
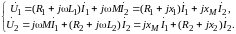 (9.2)
(9.2)
Знак
и
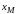 определяется выбором положительных
направлений токов
определяется выбором положительных
направлений токов
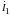 и
и
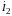 .
Для выбранных направлений токов
.
Для выбранных направлений токов
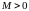 ,
если включение катушек согласное, и
,
если включение катушек согласное, и
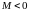 ,
если включение встречное. Способ
включения катушек устанавливается с
помощью однополярных выводов, отмеченных
”звездочками”: если токи катушек
направлены одинаково относительно
однополярных выводов (например, как
показано на рис. 9.1), то катушки включены
согласно; в противном случае включение
встречное.
,
если включение встречное. Способ
включения катушек устанавливается с
помощью однополярных выводов, отмеченных
”звездочками”: если токи катушек
направлены одинаково относительно
однополярных выводов (например, как
показано на рис. 9.1), то катушки включены
согласно; в противном случае включение
встречное.
Параметры
уравнения (9.2) могут быть определены из
двух опытов холостого хода, в одном из
которых
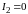 ,
в другом
,
в другом
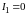 ;
осуществляют эти опыты размыканием
соответствующей пары внешних выводов
катушек. Если используют катушки
достаточно высокой добротности (
;
осуществляют эти опыты размыканием
соответствующей пары внешних выводов
катушек. Если используют катушки
достаточно высокой добротности (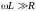 ),
то при определении индуктивностей
допустимо пренебречь активными
сопротивлениями обмоток катушек, т. е.
считать
),
то при определении индуктивностей
допустимо пренебречь активными
сопротивлениями обмоток катушек, т. е.
считать
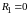 и
и
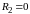 ;
ошибка при этом будет несущественной
с точки зрения инженерной практики.
Полагая в уравнениях (9.2) сначала
,
а затем
,
при условии
;
ошибка при этом будет несущественной
с точки зрения инженерной практики.
Полагая в уравнениях (9.2) сначала
,
а затем
,
при условии
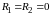 получаем соответственно:
получаем соответственно:
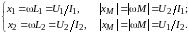 (9.3)
(9.3)
На
рис. 9.2, а показано последовательное
соединение двух индуктивно связанных
катушек. В этом случае
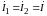 ,
,
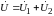 и при
из уравнений (9.2) находим выражение
эквивалентной индуктивности:
и при
из уравнений (9.2) находим выражение
эквивалентной индуктивности:
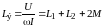 .
(9.4)
.
(9.4)
Для
параллельного соединения (рис. 9.2, б)
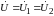 ,
,
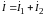 .
Разрешая систему уравнений (9.2) относительно
токов с учетом
,
можно получить выражение эквивалентной
индуктивности:
.
Разрешая систему уравнений (9.2) относительно
токов с учетом
,
можно получить выражение эквивалентной
индуктивности:
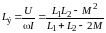 .
(9.5)
.
(9.5)
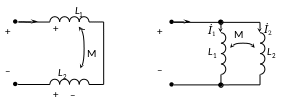
а б
Рис. 9.2
В выражениях (9.4), (9.5) при согласном и при встречном включении катушек.
Если
к выводам второй катушки присоединить
нагрузочное сопротивление
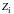 ,
получим двухобмоточный трансформатор
(рис. 9.3). В трансформаторе энергия от
источника, включенного в цепь первичной
обмотки, передается нагрузке
,
подключенной к вторичной обмотке. Эта
передача осуществляется без электрической
связи между обмотками посредством
изменяющегося потока взаимной индукции.
,
получим двухобмоточный трансформатор
(рис. 9.3). В трансформаторе энергия от
источника, включенного в цепь первичной
обмотки, передается нагрузке
,
подключенной к вторичной обмотке. Эта
передача осуществляется без электрической
связи между обмотками посредством
изменяющегося потока взаимной индукции.
Рассматривая
трансформатор как четырехполюсник,
можно его передающие свойства
характеризовать функциями передачи
напряжений и токов. Положив
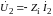 ,
из уравнений (9.2) при
получаем:
,
из уравнений (9.2) при
получаем:
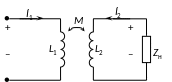
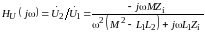 .
(9.6)
.
(9.6)
Рис. 9.3
В
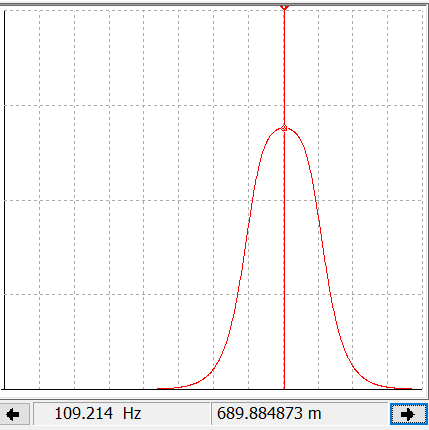
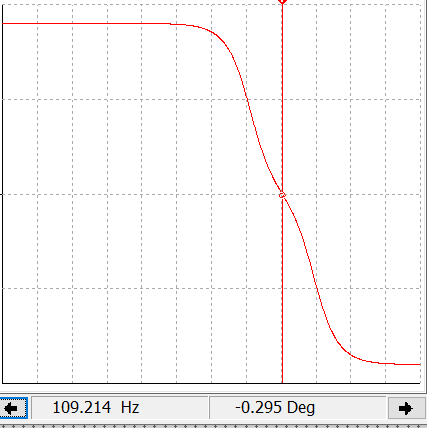
случае активной нагрузки (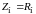 )
модуль функции передачи по напряжению
(АЧХ)
)
модуль функции передачи по напряжению
(АЧХ)
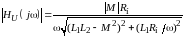 .
(9.7)
.
(9.7)
Экспериментальные исследования индуктивно-связанных катушек с применением моделирующих компьютерных программных средств Multisim.
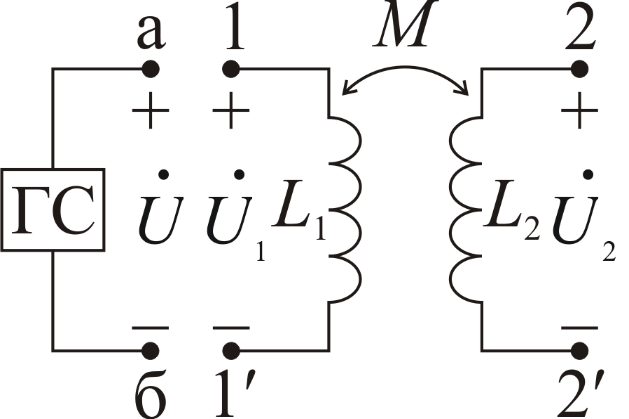
Рис. 9.5
Таблица 9.1
Номер катушки |
Наблюдения |
Вычисления |
|||||
U1, В |
U2, В |
I, мА |
X, Ом |
L, мГн |
|xM|,Ом |
|M|,мГн |
|
1 |
1 |
0.75 |
1.322 |
756,430 |
120,3895 |
567,322 |
90,29 |
2 |
0.818 |
1 |
1.442 |
693,481 |
110,3710 |
567,268 |
90,28 |
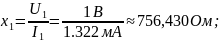
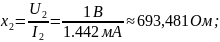
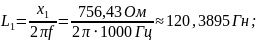
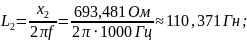

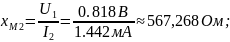
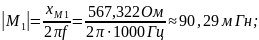
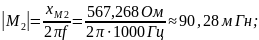
Из полученных данных видно, что такие
параметры индуктивности как
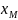 немного разнятся, но при этом
немного разнятся, но при этом
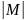 практически полностью совпали. Для
дальнейших расчётов необходимо
использовать
практически полностью совпали. Для
дальнейших расчётов необходимо
использовать
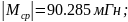
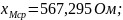
Таблица 9.2
Вид включения |
Наблюдения |
Вычисления |
|||||||
U, В |
U1, В |
U2, В |
I, мА |
I, мА |
U1, В |
U2, В |
LЭ, мГн |
||
Встречное |
1 |
0,6 |
0,4 |
3,166 |
3,1714 |
0,5998 |
0,4002 |
411,336 |
|
Согласное |
1 |
0,512 |
0,488 |
0,387 |
0,3869 |
0,5122 |
0,4878 |
50,185 |
|
Чтобы
определить тип включение необходимо
определить по
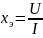 (при согласном включении увеличивается
из-за сопротивления взаимной индукции).
Из этого следует, что включение 2 –
согласное, а включение 1 – встречное.
(при согласном включении увеличивается
из-за сопротивления взаимной индукции).
Из этого следует, что включение 2 –
согласное, а включение 1 – встречное.
Далее проведём необходимые вычисления:
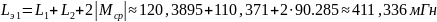
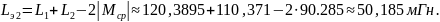
Рассчитаем
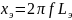 :
:
При согласном
включении:
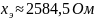
При встречном:
–
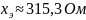 .
.
Теперь рассчитаем ток и напряжение на катушках при U = 1 В.
Согласное включение:
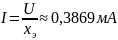
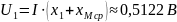
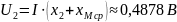
Встречное включение:
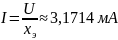
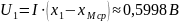
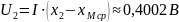
Таблица 9.3
Включение |
Наблюдения |
Вычисления |
||
U, В |
I, мА |
I, мА |
LЭ, Гн |
|
Согласное |
1,000 |
13 |
12,747 |
0,102334 |
Встречное |
1,000 |
1,555 |
1,5552 |
0,012485 |
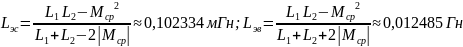
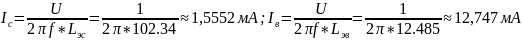
f Гц |
Rн2 |
H = U2/U1 |
Rн1 |
H = U2/U1 |
|
||||||||
U1 |
Опыт |
Расчёт |
U1 |
Опыт |
Расчёт |
f Гц |
|
|
|||||
1,303 |
1,000 |
0,073 |
0,750 |
1,000 |
0,070 |
0,750 |
1,303 |
|
|
||||
4,281 |
1,000 |
0,288 |
0,750 |
1,000 |
0,207 |
0,750 |
4,007 |
|
|
||||
5,958 |
1,000 |
0,304 |
0,750 |
1,000 |
0,277 |
0,750 |
5,577 |
|
|
||||
10,111 |
1,000 |
0,449 |
0,750 |
1,000 |
0,413 |
0,750 |
9,464 |
|
|
||||
13,171 |
1,000 |
0,522 |
0,750 |
1,000 |
0,482 |
0,750 |
12,328 |
|
|
||||
27,253 |
1,000 |
0,665 |
0,750 |
1,000 |
0,624 |
0,750 |
25,509 |
|
|
||||
225,978 |
1,000 |
0,736 |
0,723 |
1,000 |
0,690 |
0,750 |
109,214 |
|
|
||||
1874,000 |
1,000 |
0,662 |
0,301 |
1,000 |
0,618 |
0,744 |
467 |
|
|
||||
3877,000 |
1,000 |
0,517 |
0,155 |
1,000 |
0,488 |
0,729 |
905 |
|
|
||||
5051,000 |
1,000 |
0,444 |
0,120 |
1,000 |
0,419 |
0,715 |
1180 |
|
|
||||
9156,000 |
1,000 |
0,282 |
0,067 |
1,000 |
0,280 |
0,661 |
2002 |
|
|
||||
11928,000 |
1,000 |
0,242 |
0,051 |
1,000 |
0,199 |
0,586 |
2976 |
|
|
||||
39201,000 |
1,000 |
0,071 |
0,016 |
1,000 |
0,071 |
0,299 |
8571 |
|
|
||||
Нагрузка R2
Нагрузка R2
Выводы.
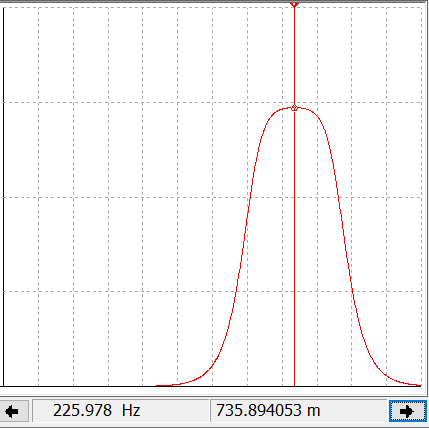
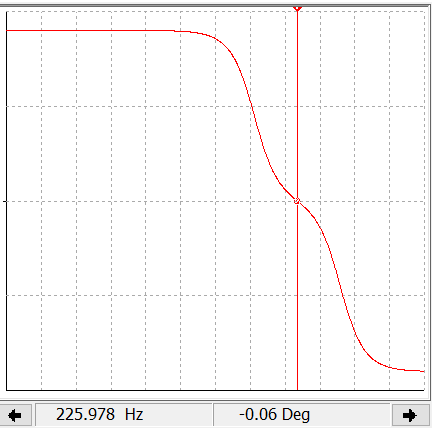
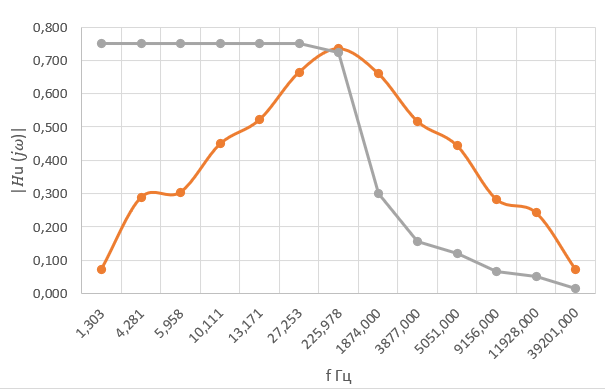
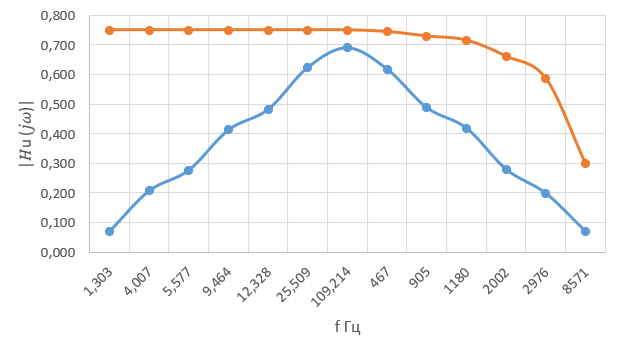
В ходе данной работы были определены параметры двух индуктивно-связанных катушек в разных подключениях: параллельно и последовательно, согласно и встречно. Найдены эквивалентная индуктивность, напряжённость и токи практическим путём. Так же были построены графики АЧХ функции передачи напряжения трансформатора (с нагрузками 200 и 1000 Ом). Можно сказать, что теоретические положения сошлись с экспериментом.
Ответы на вопросы:
1. Как установить правильность выполнения проведенных исследований?
Правильность выполнения проведённых исследований можно установить, сравнивая ранее полученные данные с текущими, например, при последовательном и параллельном соединении индуктивно связанных катушек наблюдаемая и рассчитанные силы тока должны совпадать, иначе исследования выполнены неверно.
2. Как практически разметить однополярные выводы двух индуктивно связанных катушек?
При соединение двух катушек последовательно ток в цепи больше при встречном подключении
3. При каком соотношении между параметрами катушек L1, L2, M напряжение одной из них в режиме гармонических колебаний при последовательном соединении катушек и встречном включении будет отставать от тока?
При последовательном соединении катушек у них будет общий ток:
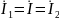 при
этом напряжение на
при
этом напряжение на
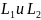 будет равно:
будет равно:
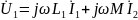 и
и
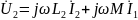 соотв.
соотв.
С учётом общего тока получаются следующие уравнения:
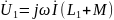 и
и
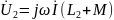 соотв.
соотв.
Исходя из вышеописанных уравнений, следует вывод, что напряжение на катушках будет отставать в следующих случаях:
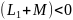 и
и
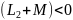 соответственно
соответственно
Что может наблюдаться только при встречном включении, т к M отрицательна
4. Почему АЧХ трансформатора падает в области низких и высоких частот? В какой частотной области исследуемый трансформатор приближается к идеальному? Почему на нулевой частоте сигнал через трансформатор к нагрузке не проходит?
Исследуемый трансформатор приближается к идеальному при нагрузке R1 на отрезке [12,328, 905] – это является полосой пропускания.
