Shevchenko / 2sem / LR10_MatlabZapiska

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра МВЭ

Отчет

По лабораторной работе №10

по дисциплине «Алгоритмы и вычислительные средства»

Тема:Алгоритмы и программы решения задач вычислительной геометрии

Студент гр. 3206		Корепанов Д. М.
Руководитель		Шевченко С. А.

Санкт-Петербург

2024

1. Цель

Изучение и программирование алгоритма построения выпуклой оболочки набора точек.

2. Постановка задачи

Заданы: множество S из n точек в двумерном пространстве; алгоритм вычисления полярного угла вектора 1-2; алгоритм построения выпуклой оболочки набора точек (Jarvis)

Найти: выпуклый многоугольник, содержащий все точки множества S

3. Алгоритм выполнения работы

1. Реализовать в Программе 1 в Matlab алгоритм вычисления полярного угла вектора 1-2 в виде функции.

2. Протестировать Программу 1 на наборе векторов, имеющих полярные углы в 45, 135, 225, 315 град.

3. Реализовать в Программе 2 в Matlab алгоритм построения выпуклой оболочки набора точек (Jarvis) и вывода результатов (m – количество вершин многоугольника).

4. Оформить отчет, включив в него основную и модифицированную Программы 1 и 2; результаты тестирования Программы 1; исходные и конечные массивы sx, sy; копию построенного в Матлаб графика, подтверждающего полученную выпуклую оболочку.

4. Основная часть

1. Вычисление полярного угла

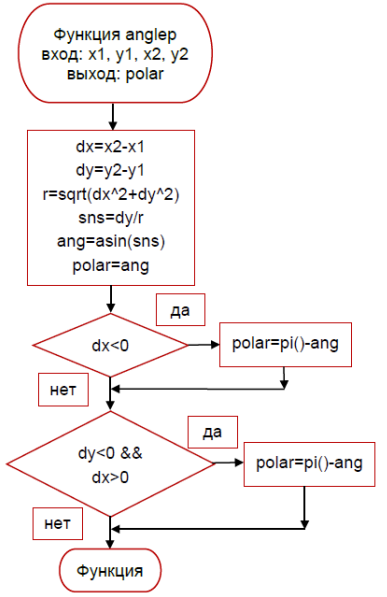
Рисунок 1 – Блок-схема алгоритма вычисления полярного угла вектора 1-2

1. Код программы

clc

clear

sx=[1, -1, -1, 1, 1];

sy=[1, 1, -1, -1, 1];

function[polar] = anglep(x1, y1, x2, y2);

dx = (x2-x1);

dy = (y2-y1);

r = sqrt((dx^2)+(dy^2));

sns = dy/r;

ang = asin(sns);

polar = ang;

if dx<0

polar = pi()-ang;

end

if dy<0 && dx>0

polar = pi()-ang;

end

end

for I=1:4;

x1=sx(I);

y1=sy(I);

x2=sx(I+1);

y2=sy(I+1);

p=anglep(x1, y1, x2, y2);

p

end

hp=compass(sx, sy);

2. Листинг результатов

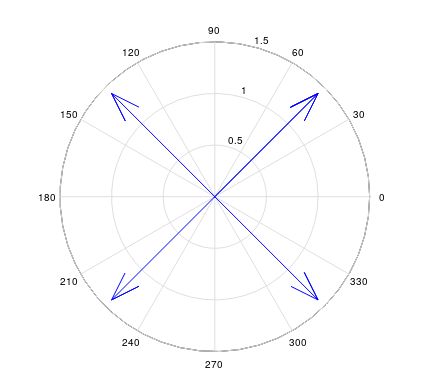
Рисунок 2 – Скриншот окна программы с результатами алгоритма

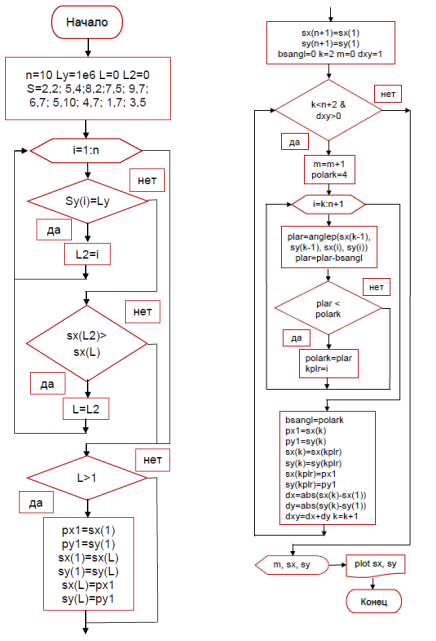
Рисунок 3 – Блок-схема алгоритма построения выпуклой оболочки набора точек (Jarvis) и вывода результатов

4.2.1. Код программы

clc;

clear all;

N = 10;

L = 1;

Ly=1e-6

L2=1

l2 = 1;

s = [2, 2; 5, 4; 8, 2;

7, 5; 9, 7; 6, 7;

5, 10; 4, 7; 1, 7; 3, 5];

sx=[2 5 8 7 9 6 5 4 1 3];

sy=[2 4 2 5 7 7 1 7 7 5];

function polar = anglePolar(x1, y1, x2, y2)

dx = x2-x1;

dy = y2-y1;

r = sqrt(dx.^2+dy.^2);

sns = dy/r;

ang = abs(asin(sns)); %Значение относительного положения точек по координате игрик в радианах

polar = ang;

if dy == 0 && dx < 0 %Находим полярные углы из положения на окружности

polar = pi();

elseif dx == 0 && dy < 0

polar = 3/2*pi();

elseif dx < 0 && dy > 0

polar = pi() - ang;

elseif dx > 0 && dy < 0

polar = 2*pi() - ang;

elseif dx < 0 && dy < 0

polar = pi() + ang;

end

end

for I = 1:N

if sy(I)<=Ly

L2 = I;

end

if sx(L2)>sx(L)

L = L2;

end

end

if L >= 1

px = sx(1);

py = sy(1);

sx(1) = sx(L);

sy(1) = sy(L);

sx(L) = px;

sx(L) = py;

end

sx(N+1) = sx(1);

sy(N+1) = sy(1);

bsangl = 0;

k = 2;

m = 0;

dxy = 1;

while (k < (N+2) && dxy > 0)

m = m+1;

polark = 100;

for i = k:(N+1)

polar = anglePolar(sx(k-1), sy(k-1), sx(i), sy(i));

if polar < polark && polar >= bsangl

polark = polar;

kplr = i;

end

end

bsangl = polark;

px = sx(k);

py = sy(k);

sx(k) = sx(kplr);

sy(k) = sy(kplr);

sx(kplr) = px;

sy(kplr) = py;

dx = abs(sx(k)-sx(1));

dy = abs(sy(k)-sy(1));

dxy = dx+dy;

k = k + 1;

end

plot(sx, sy, 'bo');

hold on;

plot(sx(1:m+1), sy(1:m+1), 'b-');

disp(m);

disp(sx);

disp(sy);

4.2.2. Листинг результатов

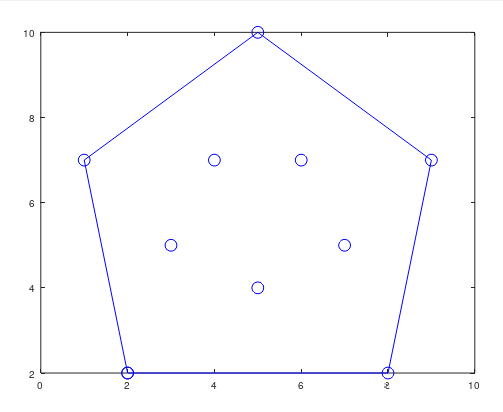
Рисунок 4 – Скриншот окна программы с результатами алгоритма

5. Вывод

В ходе выполненной работы изучены: алгоритм построения выпуклой оболочки набора точек и определения полярного угла векторов по массиву заданных точек, с выводом рисунка исполненной программы.