ОТС_11

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Факультет Сети и системы связи

Кафедра Общая теория связи

Лабораторная работа № 11

по дисциплине «Общая теория связи»:

  

«Временная дискретизация и восстановление непрерывных сигналов»

Подготовил:

студент 2-го курса,

4 бригада

Москва

2024

Цель работы

Теоретическое и экспериментальное изучение временной дискретизации непрерывных сигналов, способа восстановления исходной функции по ее отсчетам, факторов, влияющих на точность восстановления.

Рис. 1 Блок-схема лабораторного макета

Домашнее задание

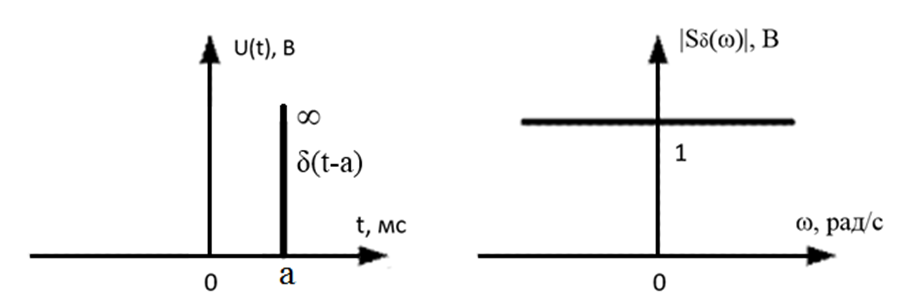
Рис. 2 График одиночного δ – импульса и его спектр

Рис. 3 График периодической последовательности δ – импульсов

t =2.5 мс

Найдем спектр периодической последовательности δ – импульсов:

Рис. 4 График спектра периодической последовательности δ – импульсов

Рис. 5 Спектр исходной непрерывной функции

Построим графики спектра АИМ-сигнала с длительностью импульсов и периодом и дискретную функцию времени, спектр которой ).

Рис. 6 Спектр дискретизированного сигнала и АИМ-сигнала

Амплитудно-частотная характеристика идеального ФНЧ выглядит:

Рис. 7. АЧХ идеального ФНЧ

_в = 2π 10² рад/с

Рис. 8 Импульсная реакция идеального ФНЧ

R₁=4 кОм; С₁ =0.25 мкФ;  = π/4t рад/c

Рис. 9 Схема RC-ФНЧ.

Амплитудно-частотная характеристика RC ФНЧ имеет вид:

Рис. 10 АЧХ идеального RC-ФНЧ

Импульсная реакция RC-фильтра:

с

Рис. 11 Импульсная реакция идеального RC-ФНЧ

Рассчитаем минимально возможную энергию E_min ошибки восстановления непрерывного сигнала в виде экспоненциального импульса

Эксперимент:

1) Временная диаграмма гармонического колебания частотой 1 кГц

2) Временная диаграмма гармонического колебания частотой 5 кГц

3) Временная диаграмма суммы непрерывного гармонических колебаний

4) Временная диаграмма дискретизирующих импульсов

5) Временная диаграмма дискретизированного сигнала

6) Временная диаграмма восстановленного сигнала на выходе RC фильтра нижних частот при С=3 мкФ

7) Временная диаграмма восстановленного сигнала на выходе RC фильтра нижних частот при С=30 мкФ

8) Временная диаграмма восстановленного сигнала на выходе RC фильтра нижних частот при С=300 мкФ

Вывод: чем выше частота дискретизации, тем более точно восстановленный сигнал соответствует исходному. При использовании RC-фильтра с большей ёмкости убираются ненужные частоты и остаётся «ступенчатый» сигнал, наиболее похож на непрерывный сигнал