ЧМ_6

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Факультет Сети и системы связи

Кафедра Информатики

Лабораторная работа № 6

по дисциплине «Численные методы»:

  

«Одномерная оптимизация»

Подготовил:

студент 2-го курса,

17 вариант

Проверил:

Юсков И.О.

Москва

2024

Индивидуальное задание к работе

Вариант 17

Решить задачу одномерной оптимизации: найти минимум функции

Применить методы золотого сечения и дихотомии

Исследование функции

Построим график функции и найдем отрезок неопределенности.

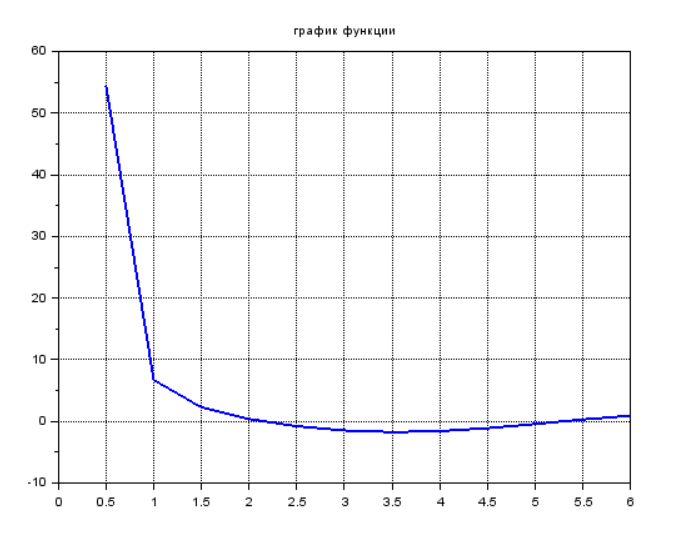
Отрезок неопределенности (отрезок, на котором есть точка минимума) – [3;4].

Проверим выполнение аналитического условия унимодальности функции на выбранном отрезке:

т.к. , sin(x) и cos(x) не обращаются в нуль одновременно

Значения сведем в следующую таблицу:

x	3.5	3.6	3.7	3.8	3.9	4
	-1.734	-1.732	-1.717	-1.686	1.641	-1.581
	-0.0907	0.0718	0.2295	0.382	0.527	0.665
	1.807	1.751	1.686	1.613	1.5304	1.439

На отрезке [3.5;4] функция монотонно возрастает, следовательно, функция f(x) - на выбранном отрезке унимодальная.

Метод золотого сечения

Проведем 3 итерации и результаты занесем в таблицу 1.

1 итерация:

Тогда

;

2 итерация:

Тогда

;

3 итерация:

Тогда

;

Таблица 1 – Расчётные данные для метода ЗС

N	a	b
0	3.5	4
1
2
3							0.2

Хmin = 3,7

Ymin=0.997

Метод дихотомии

Проведем 3 итерации и результаты занесем в таблицу 1.

1 итерация:

Тогда

;

2 итерация:

Тогда

;

3 итерация:

Тогда

;

Таблица 2 – Расчётные данные для метода дихотомии

N	a	b
0	1	5.5					4.5
1							2.26
2
3

В результате расчета на ПК при N=13 длина отрезка равна 0.00014. Точность достигнута при N=14, т. е. расчет совпадает с теоретической оценкой

Решение одномерной оптимизации с помощью программирования

Решение одномерной оптимизации метод золотого сечения и дихотомии на Scilab.

x=[0:0.5:6]; y=sin(x+1).*exp(x./2); plot(x,y) xtitle('График функции');

deff('y=f0(x)','y=sin(x+1)*exp(x/2)'); //Описание целевой функции function [f, g, ind]=costf(x, ind) f=f0(x) g=numderivative(f0,x) endfunction x0=3; [fmin,xmin]=optim(costf,x0) fmin = -7.2170517 xmin = 4.1760366

Решение метода золотого сечения на ПК:

function [f1]=y(x) f1=cos(x+1)*exp(2/x)-((2*exp(2/x)*sin(x+1))/x^2) endfunction function [f2]=y2(x) f2=(-x1.^4.*exp(2./x1).*sin(x1+1)-4.*x1.*x1.*exp(2./x1).*cos(x1+1)+4.*exp(2./x1).*sin(x1+1))./(x1.^4) endfunction //Метод золотого сечения eps=10^-4; k1=0.382; k2=0.618; a=3; b=4; h=0; d = eps / 5 x1 = a + k2 * (b - a); x2 = a + k1 * (b - a); f1 = y(x1); f2 = y2(x2); n=0; while (abs(b-a)>eps) then n=n+1; if f1<f2 then b=x2; f2=f1; x1=a+k1*(b-a); f1=y(x1); else a=x1; x1=x2; f1=f2; x2=a+k2*(b-a); f2=y2(x2); end z=[n,a,b,f1,f2,x1,x2] end

Результат работы программы

n a b f1 f2 x1 x2 18. 3.6179935 3.61808 0.1006092 0.0283006 3.6180266 3.61808

Вывод: Выполняя эту лабораторную работу, мы изучили методы решения одномерной оптимизации: метод золотого сечения и метод дихотомии. При выполнении ручного расчета результаты совпали с машинным вычислением.