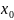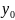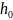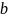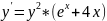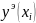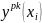ЧМ_5
.docx
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Факультет Сети и системы связи
Кафедра Информатики
Лабораторная работа № 5
по дисциплине «Численные методы»:
«Методы решения обыкновенных дифференциальных уравнений»
Подготовил:
студент 2-го курса,
17 вариант
Проверил:
Москва
2024
Индивидуальное задание к работе
№ |
Уравнение |
|
|
|
a |
|
|
|
0 |
-1 |
0.4 |
0 |
1.2 |
где
–
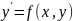дифференциальное уравнение
[a, b]– интервал, где ищется решение дифференциального уравнения
, – начальные условия
– шаг интегрирования
Выполнение задания:
Решение ОДУ аналитическим методом
Найдем
точное аналитическое решение заданного
дифференциального уравнения методом
разделения переменных. Для этого
запишем уравнение в виде
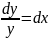и проинтегрируем с учетом начальных
условий
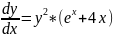
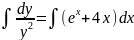
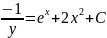
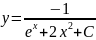
Из
начальных условий следует, что с=0. Тогда
аналитическое решение дифференциального
уравнения
.
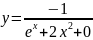Вычислим в сценарии значения полученного решения y(xi) на отрезке [0;1.2] с шагом изменения аргумента h=0.4:
xi |
y(xi) |
0 |
-1 |
0.4 |
-0.55193 |
0.8 |
-0.285263 |
1.2 |
-0.161287 |
Решение ОДУ методом Эйлера
Вычислим
значение численного решение ОДУ методом
Эйлера в точках отрезка [0;1.2] с шагом
h=0.4.
Общая формула для определения очередного
значения функции по методу Эйлера
,
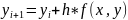где
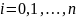
xi |
|
0 |
-1 |
0.4 |
-0.6 |
0.8 |
-0.15478 |
1.2 |
-0.10279 |
Вычислим
значение погрешностей
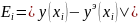для
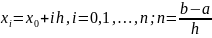
xi |
Ei |
0 |
0 |
0.4 |
0.04807 |
0.8 |
0.13049 |
1.2 |
0.058 |
Решение ОДУ методом Рунге-Кутта 4-го порядка
Вычислим
в программе значения численного решения
ОДУ с точностью 10-4,
и получим решение в точках отрезка
[0;1.2]с шагом h=0.4
(
)
методом Рунге-Кутта 4-го порядка, используя
формулы:
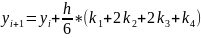
где
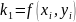
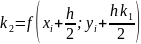
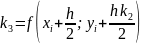
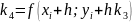
xi |
|
0 |
-1 |
0.4 |
-0.55178 |
0.8 |
-0.28505 |
1.2 |
-0.10279 |
Вычислим
в сценарии значения погрешностей
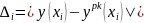
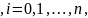
xi |
|
0 |
0 |
0.4 |
0.00015 |
0.8 |
0.00022 |
1.2 |
0.00022 |
Сделаем сводку решений ОДУ всеми методами в одну таблицу.
xi |
y(xi) |
|
Ei |
|
|
0 |
-1 |
-1 |
0 |
-1 |
0 |
0.4 |
-0.55193 |
-0.6 |
0.04807 |
-0.55178 |
0.00015 |
0.8 |
-0.285263 |
-0.15478 |
0.13049 |
-0.28505 |
0.00022 |
1.2 |
-0.161287 |
-0.10279 |
0.058 |
-0.10279 |
0.00022 |
Решение ОДУ с помощью программирования
Решение ОДУ с помощью Scilab представлен ниже.
Код сценария 1:
function yd=f(x, y) yd=y*y*(exp(x)+4*x) endfunction z=ode(y,x0,x,f); disp("Решение ОДУ функцией ode"); zz=[x;z]; zz' //таблица решения ОДУ функций ode |
Код рабочего окна:
--> y=-1; --> x0=0; --> x=0:0.4:1.2; --> exec('C:\Users\orliu\Desktop\Работы\ЧМ\5.sce', -1) "Решение ОДУ функцией ode" --> ans ans = 0. -1. 0.4 -0.5519298 0.8 -0.2852627 1.2 -0.1612873 |
Решение ОДУ при помощи C++
#pragma once #include <cmath>
namespace Project1 {
using namespace System; using namespace System::ComponentModel; using namespace System::Collections; using namespace System::Windows::Forms; using namespace System::Data; using namespace System::Drawing;
/// <summary> /// Сводка для MyForm1 /// </summary> ------------------------------------------------------------------- #pragma endregion double Vvod(TextBox^ t) { return Convert::ToDouble(t->Text); }
double f(double x, double y) { return y*y*(exp(x)+4*x);
} double Yt(double x) { return -1/(exp(x)+2*x*x); } double Yrk4(double x, double y, double h, int m) { double Yr = y; for (int i = 1; i <= m; i++) { double k1 = f(x, Yr) * h; double k2 = f(x + h / 2, Yr + k1 / 2) * h; double k3 = f(x + h, Yr + 2 * k2 - k1) * h; Yr = Yr + (k1 + 4 * k2 + k3) / 6; x = x + h; } return Yr; } double Runge4(double x0, double y0, double h0, double eps, int &m) { double x = x0; double y = y0; double h = h0; m = 1; double Yrk = Yrk4(x, y, h, m); double Yrk0; do { Yrk0 = Yrk; h = h / 2; m = 2 * m; Yrk = Yrk4(x, y, h, m); } while (abs(Yrk - Yrk0) > eps); return Yrk0; } private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) { double a, b, h, y0, eps; a = Vvod(textBox1); b = Vvod(textBox2); h = Vvod(textBox3); eps = Vvod(textBox4); y0 = Vvod(textBox5);
double x = a; double Ye = y0; double Yrk = y0; double Y = Yt(x); int n = (int)((b - a) / h) - 1; int m = 0; ; listBox1->Items->Clear(); String^ s = " x Yt Ye Yrk m ErrorYe ErrorYrk "; listBox1->Items->Add(s); s = x.ToString("F5") + " " + Y.ToString("F5") + " " + Ye.ToString("F5"); s = s + " " + Yrk.ToString("F5") + " " + m.ToString("F5"); s = s + " " + abs(Y - Ye).ToString("F5") + " " + abs(Y - Yrk).ToString("F5"); listBox1->Items->Add(s);
for (int i = 0; i <= n; i++) { Ye = Ye + f(x, Ye) * h; Yrk = Runge4(x, Yrk, h, eps, m); x = x + h; Y = Yt(x); s = x.ToString("F5") + " " + Y.ToString("F5") + " " + Ye.ToString("F5"); s = s + " " + Yrk.ToString("F5") + " " + m.ToString("F5"); s = s + " " + abs(Y - Ye).ToString("F5") + " " + abs(Y - Yrk).ToString("F5"); listBox1->Items->Add(s); }
} }; } |
|
Результат работы программы:
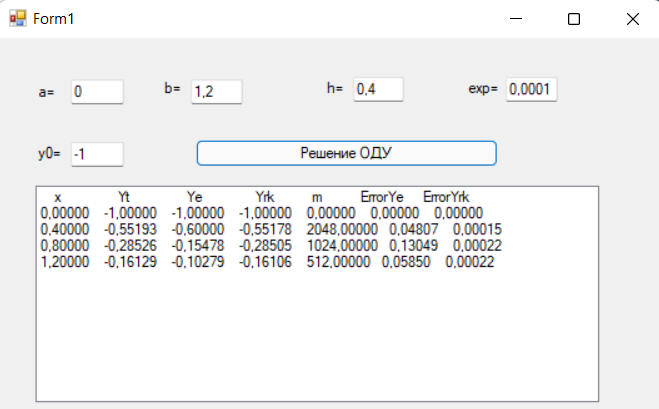
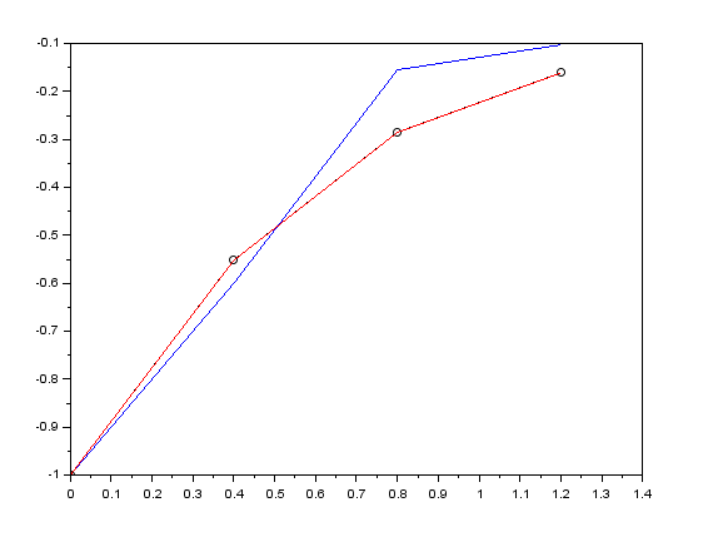
Вывод: Выполняя эту лабораторную работу, мы изучили методы решения обыкновенных дифференциальных уравнений и рассчитали погрешности. При выполнении ручного расчета ОДУ результаты совпали с машинным вычислением.