МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Факультет Сети и системы связи

Кафедра Информатики

Лабораторная работа № 4

по дисциплине «Численные методы»:

  

«Численное интегрирование»

Подготовил:

студент 2-го курса,

17 вариант

Проверил:

Юсков И.О.

Москва

2024

Оглавление

Индивидуальное задание к работе 2

Решение интеграла с помощью С++ 4

Индивидуальное задание к работе

Рисунок 1 Индивидуальное задание к работе

Где в столбцах t и m. 1 – интегрирование методом средних прямоугольников, 2 – метод трапеций; a и b – пределы интегрирования; f(x) = 5sin³(x)+cos³(x) – подынтегральная функция; h₀ – начальный шаг интегрирования

Выполнение задания:

Интегрирование методом средних прямоугольников (m = 1)

Вычисление интегралов с шагом h₀ = 0.25 и h₀/2 = 0.125 (I_h0 и I_h0/2) и оценка его погрешности по правилу Рунге

Правило Рунге применяют для вычисления погрешности путём двойного просчёта интеграла с шагами h/2 и h, при этом погрешность вычисляется по формуле

Полагают, что интеграл вычислен с точностью E, если |R|<E тогда I=I_h/2+R, где I – уточненное значение интеграла, p – порядок метода.

Вычислим интеграл по формуле средних прямоугольников и оценим погрешность интегрирования методом двойного просчёта:

Решение интеграла с помощью программы Scilab:

deff('y=f(x)','y=(5*(sin(x)^3)+(cos(x)^3))'); a=1;b=2; [s,ir]=intg(a,b,f) s = 4.4150773 ir = 4.902D-14

Интегрирование методом трапеций (t = 2)

Здесь мы используем метод трапеций, вычисляя интеграл с точность 10^-4

n=4

Необходимая точность

Решение интеграла с помощью С++

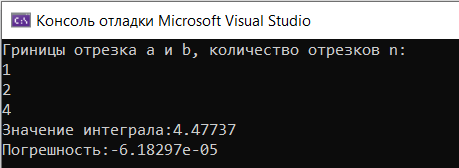
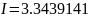Вывод: результаты интегрирования подынтегральной функции на отрезке   методами трапеций ( = 12.861; =5.721405; R=-2.379865; I=3.341540), средних прямоугольников ( ; ; ) и методом, заложенным в функции intg() пакета Scilab, совпали в пределах допустимой погрешности - значит, расчёты проведены верно.