МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Факультет Сети и системы связи

Кафедра Информатики

Лабораторная работа № 2

по дисциплине «Численные методы»:

  

«Интерполяция функций»

Подготовил:

студент 2-го курса,

17 вариант

Проверил:

Москва

2024

Оглавление

Задание 2

Метод Ньютона 3

Полином Лагранжа 5

Задание

Метод Ньютона

По таблице индивидуального задания определяем точку интерполяции для формулы Ньютона x = a = 0.42.

Далее необходимо подобрать 4 узла из предложенной таблицы так, что точка a = 0.42 оказалась внутри таблицы, и узлы были наиболее близки к этой точке. В таблице 1 представлены выбираемые узлы.

7	0.40	-3.6320
8	0.45	-3.4890
9	0.50	-3.3250
10	0.55	-3.1385

Изменим нумерацию узлом интерполяции для использования их в интерполяционных формулах и занесем в таблицу 2.

k	0	1	2	3
xk	0.40	0.45	0.50	0.55
yk	-3.6320	-3.4890	-3.3250	-3.1385

Таблица 2 – Перенумерованные узлы

	x	Y	Δy
0	0.40	-3.6320	0.143	0,021	0,0015
1	0.45	-3.4890	0,164	0.0225
2	0.50	-3.3250	0.1865
3	0.55	-3.1385

Таблица 3 – Конечные разницы

Запишем 1–ю интерполяционную формулу Ньютона для полиномов 1–й, 2–й и 3–й степени и выполним расчеты по ним.

Определим значение q:

Значение полинома 1-й степени в т. x=0,42:

Значение полинома 2-й степени в т. x=0.42:

Значение полинома 3-й степени в т. x=0,42:

Найдем явные выражения для полиномов 1, 2 и 3 степени по формуле:

Тогда:

-4.2+0.5x+1.5 +2

Занесем результаты в таблицу 4 и вычислим оценки погрешности полученных значений для полиномов 1–й и 2–й степени:

Занесем результаты в таблицу 4 и вычислим оценки погрешности полученных значений для полиномов 1–й и 2–й степени:

Степень многочлена k	Rk(x)	Оценка погрешности
1		0.00546
2		0.000084
3		–

Таблица 4 – Оценка погрешностей

Вывод: Получены выражения для интерполяционных многочленов 1, 2 и 3-ей степени и их значения в точке а. Можно утверждать, что разность между точным (неизвестным) значением функции и значением интерполяционного полинома в точке x=0.42 после 3-х итераций не превышает 0,001.

Полином Лагранжа

Из таблицы индивидуального задания выбираем точку интерполяции для интерполяции полиномом Лагранжа: x=b=1.02.

Далее необходимо подобрать 4 узла из предложенной таблицы так, что точка b=1.02 оказалась внутри таблицы, и узлы были наиболее близки к этой точке. В таблице 5 представлены выбираемые узлы.

19	1.00	-0.2000
20	1.05	0.2940
21	1.10	0.8270
22	1.15	1.4005

Таблица 5 – Выбранные узлы

Перенумеруем узлы интерполяции и занесем их в таблицу 6.

k	0	1	2	3
xk	1.00	1.05	1.10	1.15
yk	-0.2000	0.2940	0.8270	1.4005

Таблица 6 – Перенумерованные узлы

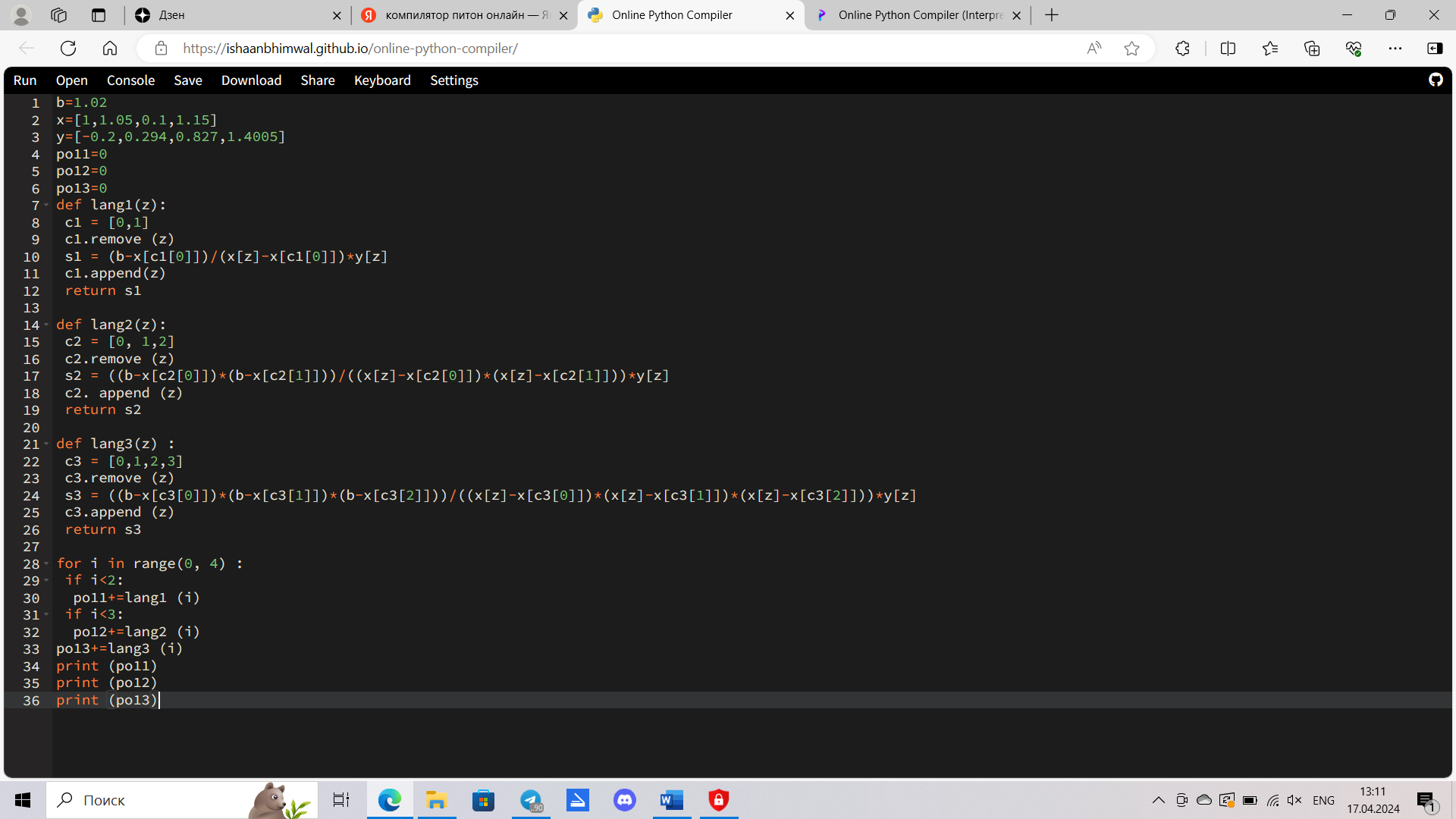
Занесем результаты в таблицу 6 и вычислим оценки погрешности полученных значений для многочленов 1–й и 2–й степени:

Степень многочлена k	Lk(x)	Оценка погрешности
1		0.00697
2		0.03972
3		-

Таблица 7 – Оценка погрешностей

Вывод: Получены выражения для интерполяционных полиномов 1, 2 и 3-ей степени и их значения в точке b.