МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Факультет Сети и системы связи

Кафедра Информатики

Лабораторная работа № 1

по дисциплине «Численные методы»:

  

«Методы решения нелинейный уравнений»

Подготовил:

17 вариант

Проверил:

Юсков И.О.

Москва

2024

Оглавление

1 Задание 1

2 Отделение корней. 2

3 Метод итераций. 3

4 Метод половинного деления 4

Вывод 6

1 Задание

1. Выбрать индивидуальное задание по указанию преподавателя из табл. 1.2-1:

· нелинейное уравнение;

· метод решения нелинейного уравнения для «ручного расчета»;

· метод решения нелинейного уравнения для «расчета на ПК».

2. Отделить корни уравнения.

3. Провести исследование нелинейного уравнения для его решения.

· проверить выполнение условий сходимости вычислительного процесса, в случае расходящегося процесса – сделать необходимые преобразования для обеспечения сходимости;

· выбрать начальное приближение;

· сформулировать условия окончания этапа уточнения корня.

4. Провести «ручной расчет» трех итераций.

5. Оценить погрешность результата «ручного расчета».

6. Составить схему алгоритма, написать программу для решения нелинейных уравнений для «расчета на ПК» и провести контрольное тестирование программы, воспользовавшись исходными данными и результатами примера из п.п.1.2-1.5.

7. Решить нелинейное уравнение с точностью, воспользовавшись написанной программой для «расчета на ПК».

8. Построить зависимость числа итераций от заданной точности –n(E).

1.Индивидуальное задание: (уравнение, методы решения).

2– итераций ,1-половинное деление

2 Отделение корней.

Произведем отделение корней при помощи программы MathCad.

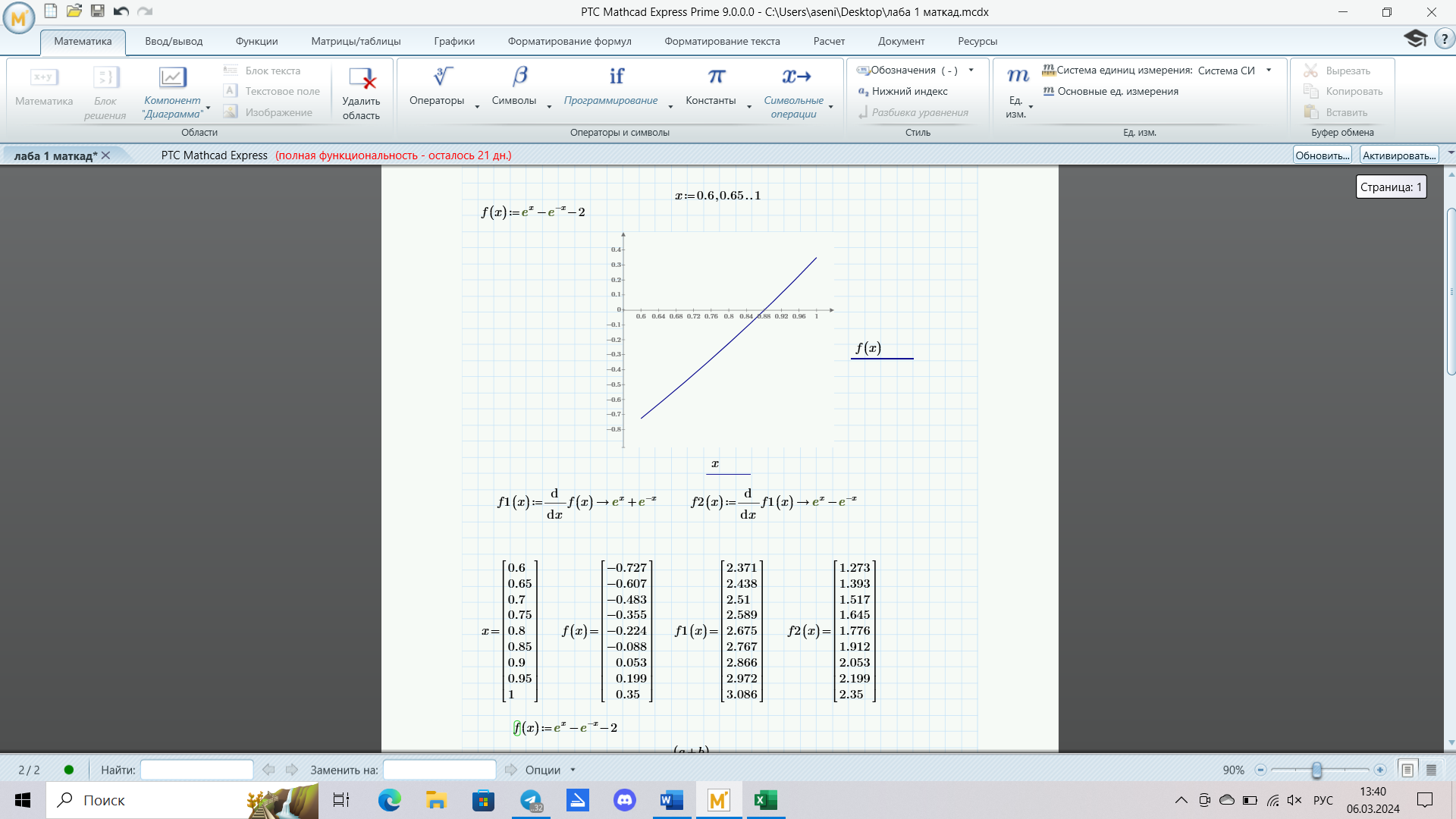
На интервале [0,8 ; 0,9] функция имеет один корень, поэтому мы можем использовать этот интервал для расчётов и в этом случае f’(x) и f”(x) непрерывны и знакопостоянны и f(0,8)*f(0,9)<0

3 Метод итераций.

Исходное уравнение:

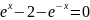
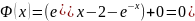
Сделаем замену

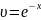
Получим

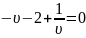
Делаем обратную замену

или x=-log(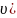

Тогда получим:

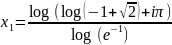
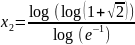
Тогда получим численный ответ:

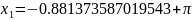
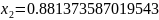
Первый корень не подходит так как он отрицательный.

Значит в ответ пойдёт второй корень

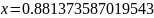
4 Метод половинного деления

Блок-схема

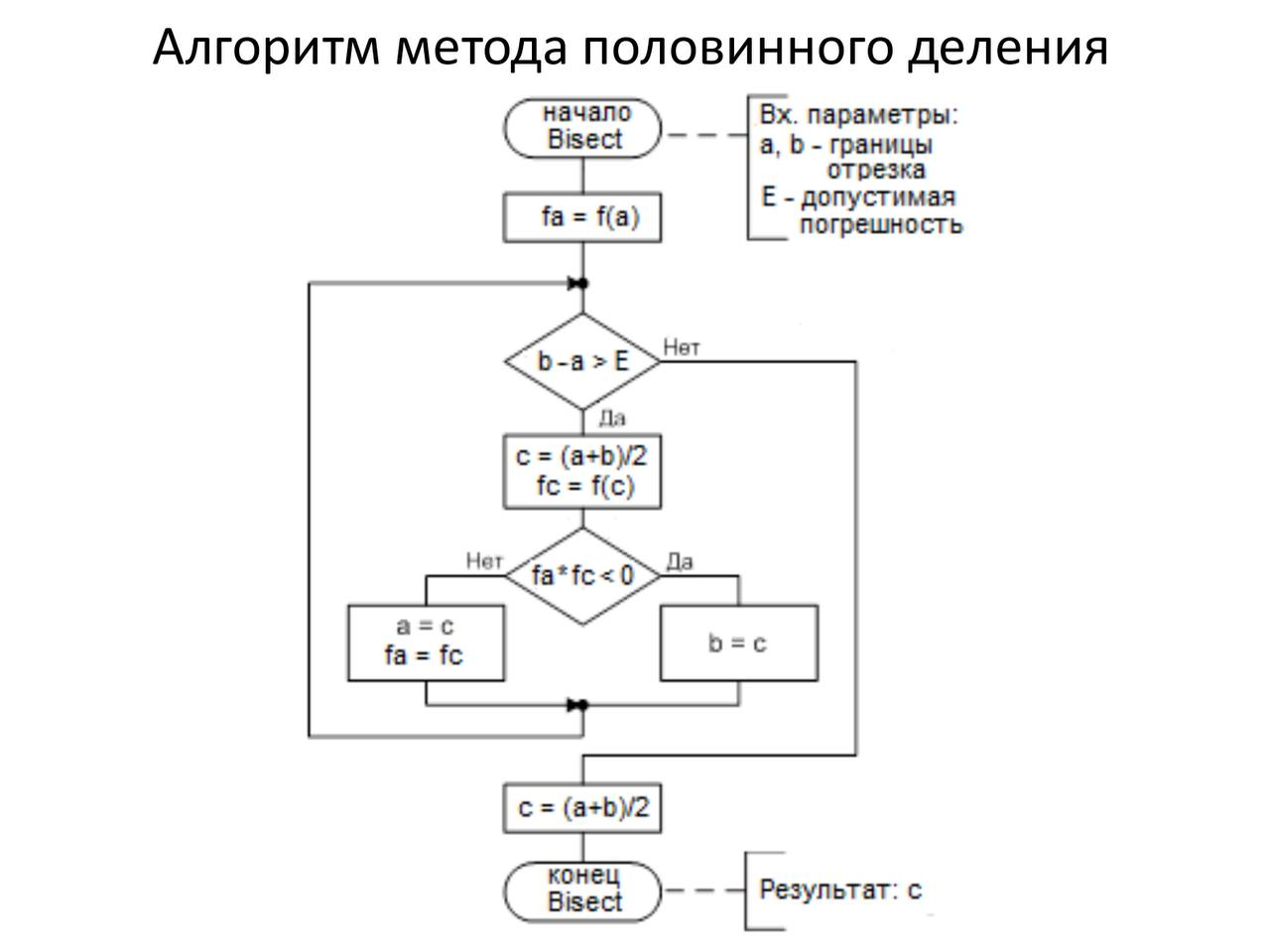
Пишем программу вводя переменные интервала известные из Рис. 1. и указывая нужную нам погрешность (точность) 10^-4.

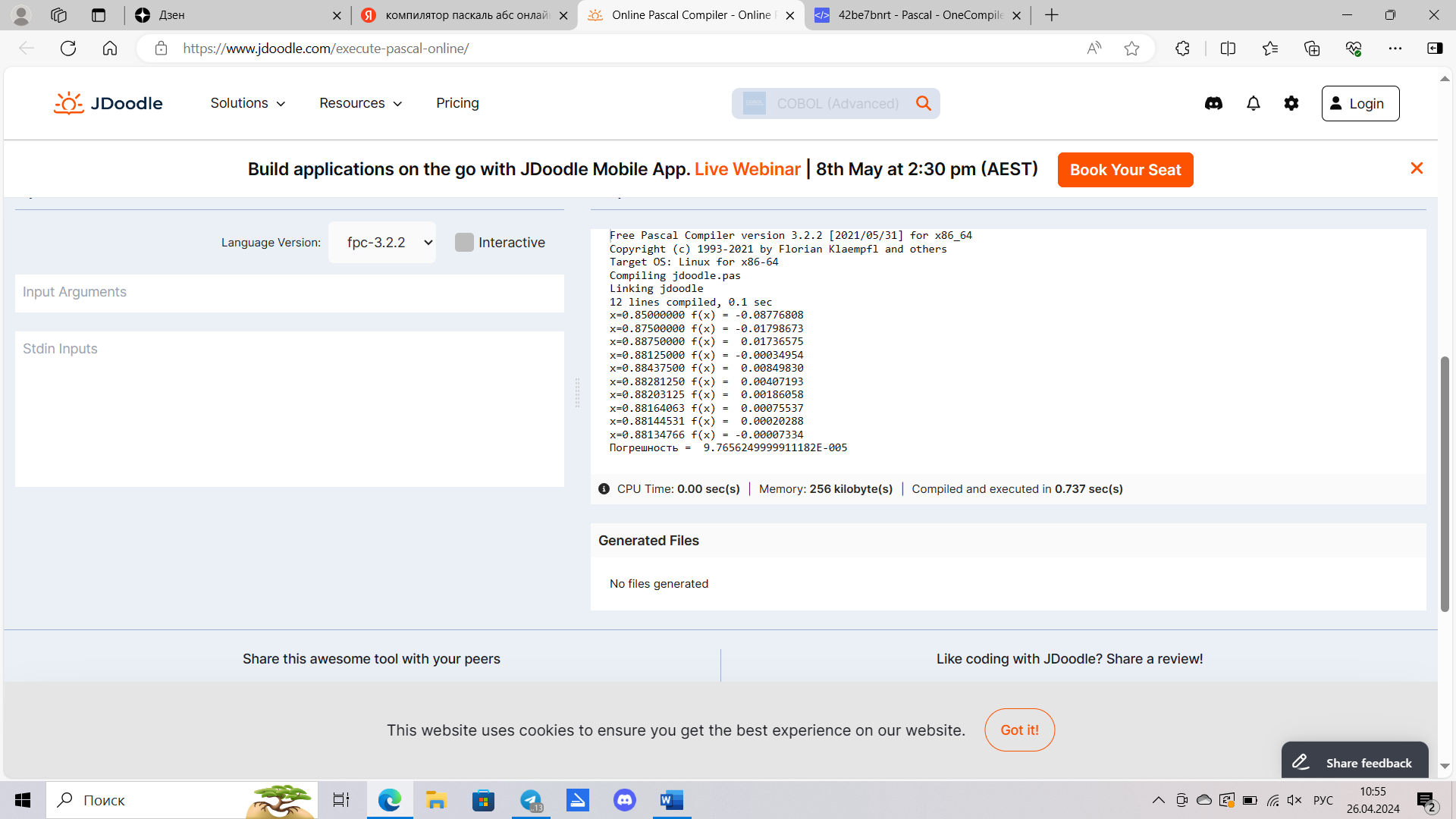
Мы получили нужную нам погрешность (точность) и программа прекратила работу.

k	x	f(x)
10	0.88134766	-0.00007334

Зависимость функции от x после 10 итерации.

Вывод

В результате локализации корней, функция f(x)=e^x-e^-x-2 на промежутке х = [0.8; 0.9] меняет знак, следовательно, уравнение имеет хотя бы один корень и первая и вторая производные f1(x) и f2(x) знакопостоянны и непрерывны на всем отрезке. После проведения итераций двумя методами, приближение к корню получилось x = 0.88134766, а погрешность составила 9.7656249999911182*10^-5.

Лично я научился локализовать корни, применять метод Итераций вручную и понял принцип его работы, с методом половинного деления всё оказалось ещё проще, главное знать какая точность нужна или же сколько итераций нужно сделать.