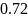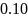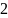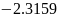МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное

бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ

Кафедра: Информатика

Лабораторная работа № 2

по дисциплине «Численные методы»:

«Интерполяция функций»

Вариант 2

Выполнил:

Проверил: Старший преподаватель Юсков И. О.

Доцент кафедры кандидат технических наук Аляпкин В. В.

Москва г.

Оглавление

1. Задание 3

2. Индивидуальное задание 4

3. Компьютерный расчёт Ньютона 5

4. Ручной расчёт Лагранжа 8

1. Задание

1. Выбрать индивидуальное задание из табл.1.3-1 и табл. 1.3-2 для решения задач интерполяции:

• из табл. 1.3-1 выбираем значения параметров t1 и t2, а также значения x=a (для построения многочлена Ньютона) и x=b (для построения многочлена Лагранжа);

• из табл. 1.3-2 в соответствии с методикой выбора узлов интерполяции по значению x=a выбираем узлы интерполяции (из отрезка [0.05;1.55] – область задания интерполируемой функции) и значения функции в этих узлах. Число узлов определяется заданной степенью интерполяционного многочлена в соответствии с п.2 и п.3.

Следует обратить внимание, что:

• если точка x=a расположена ближе к левому концу отрезка, выбираемого из табл.1.3-2, то для построения первой формулы Ньютона необходимо выбрать узлы 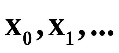  (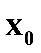  - ближайший к точке x=a узел слева);

• если точка x=a расположена ближе к правому концу отрезка, выбираемого из табл.1.3-2, то используют вторую формулу Ньютона и необходимо выбрать узлы 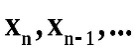  (x_n – ближайший к точке x=a узел справа);

• если точка x=a расположена примерно в середине таблицы, то следует выбрать ту формулу, которая обеспечит меньшую погрешность.

2. Выполнить линейную, квадратичную и кубическую интерполяцию функции 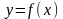  , заданной таблично (табл.1.3-2), указанным в табл.1.3-1 методом (значение t1) «расчет на ПК»:

• составить схему алгоритма и программу решения задачи интерполяции и провести контрольное тестирование на данных примера, разобранного в п. 5;

• вычислить значение интерполирующего многочлена Ньютона в точке   ; для многочлена Лагранжа в точке   ;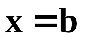

• провести оценку погрешности интерполяции по формулам практической оценки погрешности.

3. Построить интерполяционный многочлен второй степени (Ньютона или Лагранжа в зависимости от значения t2) в явном виде (ручной расчет). Вычислить значения построенного многочлена во всех выбранных узлах интерполяции. Сравнить полученные результаты с таблично заданными значениями.

2. Индивидуальное задание

№ варианта	Интерполяционный многочлен
	Ньютона		Лагранжа
2		на компьютере		ручной расчёт

Выбор и нумерация узлов для формулы Ньютона Для ручной интерполяции в точке 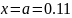по 1-й формуле Ньютона выбираем 4 узла из таблицы 2-2 так, чтобы точка оказалась между узлами с номерами с 1 по 2 и добавляем узлы вправо:

Таблица 1.1 – Узлы

№ узла
1
2
3
4

Выбор точек определяется тем, чтобы при решении задачи интерполяции в точке по 1-й формуле Ньютона с заданной точностью добавлять узлы вправо относительно точки . Изменим нумерацию узлом интерполяции для использования их в интерполяционных формулах и занесём в таблицы вида 2-3:

Таблица 1.2 – Перенумерованные узлы

3. Компьютерный расчёт Ньютона

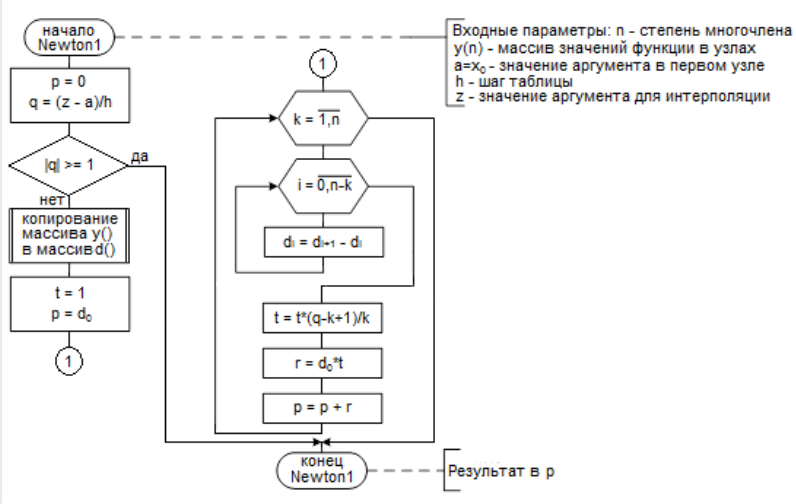Рисунок 1 – Блок-схема интерполяции в точке по 1-й формуле Ньютона

Рисунок 2 – Код программы на Python

Таблица 1.3 – Оценка погрешности

Степень многочлена		Погрешность
1
2
3		—

Вывод.

Получены выражения для интерполяционных многочленов 1, 2 и 3-ей степени и их значения в т. а. Можно утверждать, что разность между точным значением функции и значением функции в т. x=0.11 после 3-х итераций не превышает 0.000072.

4. Ручной расчёт Лагранжа

Для ручной интерполяции в точке x=b= 0.72 по формуле Лагранжа выбираем из таблицы 2-2 узлы так, чтобы точка b=0.72 оказалась в центре отрезка интерполяции. Узлы с номерами: 12-15:

Таблица 2.1 – Узлы

12	0.65	-2.692
13	0.7	-2.429
14	0.75	-2.1375
15	0.8	-1.816

Таблица 2.2 – Перенумерованные узлы

k	0	1	2	3
xk	0.75	0.7	0.8	0.65
yk	-2.1375	-2.429	-1.816	-2.692

Выполним ручной расчёт в программе Mathcad, задаем переменные из таблицы 2.2.:

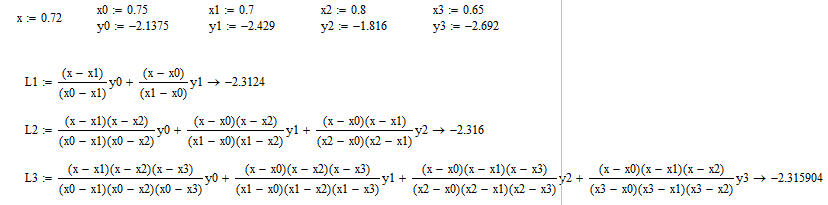Найдём явные выражения для полиномов 1,2 и 3 степеней:

Таблица 2.3 – Оценка погрешности

Степень многочлена k	Lk(x)	Оценка погрешности
1		0,0036
2		0,000096
3		-

Вывод.

Получены выражения для интерполяционных полиномов 1, 2 и 3-ей степени и их значения в точке b