
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Инженерная школа природных ресурсов
Отделение химической инженерии
18.03.01 “Химическая технология”
ЛАБОРАТОРНАЯ РАБОТА № 5
МОДЕЛИРОВАНИЕ КИНЕТИКИ ГОМОГЕННЫХ ХИМИЧЕСКИХ РЕАКЦИЙ
Вариант - 24
по дисциплине:
Моделирование химико-технологических процессов
Исполнитель:
|
|
||||
студент группы |
2Д12 |
|
Чижова Анастасия Васильевна |
|
24.04.2024 |
|
|
|
|
|
|
Руководитель:
|
Мойзес Ольга Ефимовна |
||||
преподаватель |
|
|
|
|
|
|
|
|
|
|
|
Томск - 2024
Цель работы:
Освоить статистические методы обработки экспериментальных данных пи исследовании химических процессов.
Получить вид теоретической зависимости физико-химических (теплофизических) свойств соединения и проверить соответствие полученного уравнения регрессии эксперименту.
Обработать экспериментальные данные ХТП, получить вид функциональной зависимости и оценить ошибку аппроксимации.
Теоретическая часть
Экспериментально-статистические модели
При
отсутствии достаточного объема информации
о моделируемом объекте уравнения
математического описания могут
представлять собой систему эмпирических
зависимостей, полученных в результате
статистического обследования объекта,
и имеют вид регрессионных соотношений
между входными и выходными параметрами
объекта. В этом случае в структуре
уравнений статистических моделей не
отражаются физические свойства объекта
моделирования. Основным источником
информации является эксперимент, а
обработка экспериментальных данных
осуществляется методами теории
вероятностей и математической статистики.
Объект представляется в виде «черного
ящика» (рис. 1).
Рисунок 1 – Схематическое изображение объекта
Математической
моделью служит функция отклика,
связывающая выходной параметр с входными:

или
в виде полинома:

Поскольку
в реальном процессе всегда существуют
«шумы», изменение величины y носит
случайный характер, поэтому при обработке
экспериментальных данных получаются
так называемые выборочные коэффициенты
регрессии
 ,
являющиеся оценками теоретических
коэффициентов
,
являющиеся оценками теоретических
коэффициентов
 .
Уравнение регрессии, полученное на
основании опыта, запишется следующим
образом:
.
Уравнение регрессии, полученное на
основании опыта, запишется следующим
образом:

Вид уравнения регрессии обычно задается.
Для получения статистических моделей в виде полиномов на основе данных, собранных в пассивном эксперименте, используют методы корреляционного и регрессионного анализов.
Методы корреляционного и регрессионного анализа
Методы корреляционного и регрессионного анализов широко применяются для выявления и описания зависимостей между случайными величинами по экспериментальным данным и базируются на теории вероятности и математической статистике.
К орреляционный
анализ основывается на предпосылке о
том, что переменные величины y (выходной
параметр) и xi
(факторы) являются случайными величинами
и между ними может существовать так
называемая корреляционная связь, при
которой с изменением одной величины
изменяется распределение другой. Для
количественной оценки тесноты связи
служит выборочный коэффициент корреляции.
орреляционный
анализ основывается на предпосылке о
том, что переменные величины y (выходной
параметр) и xi
(факторы) являются случайными величинами
и между ними может существовать так
называемая корреляционная связь, при
которой с изменением одной величины
изменяется распределение другой. Для
количественной оценки тесноты связи
служит выборочный коэффициент корреляции.
где
 ,
,
 ,
,
 выборочные
дисперсии:
выборочные
дисперсии:
 ,
,
 .
.
При вычислении коэффициента корреляции удобно пользоваться следующими формулами:
|
|


где N – число опытов.
Выявить наличие или отсутствие корреляции между двумя величинами можно путем визуального анализа полей корреляции и оценкой величины выборочного коэффициента корреляции.
 На
рис. 2 показаны примеры корреляции между
случайными величинами.
На
рис. 2 показаны примеры корреляции между
случайными величинами.
Рис.2. Виды корреляции между случайными величинами
Для
независимых случайных величин коэффициент
корреляции равен нулю, но он может быть
равен нулю для некоторых зависимых
величин, которые при этом называются
некоррелированными. Коэффициент
корреляции характеризует не всякую
зависимость, а только линейную. Если
случайные величины x и y связаны точной
функциональной линейной зависимостью
 ,
то
,
то
 .
В общем случае, когда величины связаны
произвольной стохастической зависимостью,
коэффициент корреляции может иметь
значение в пределах
.
В общем случае, когда величины связаны
произвольной стохастической зависимостью,
коэффициент корреляции может иметь
значение в пределах
 .
.
Регрессионный анализ –(рассматривает) связь между зависимой (случайной) величиной y и независимыми (неслучайными) переменными x1,…,xi.
Эта связь представляется с помощью математической модели, т. е. уравнения, которое связывает зависимую и независимую переменные.
Обработка экспериментальных данных при использовании корреляционного и регрессионного анализа дает нам возможность построить статистическую математическую модель в виде уравнения регрессии.
По
данной выборке объема n найти уравнение
приближенной регрессии и оценить
допускаемую при этом ошибку, то есть
нужно найти
 .
Эта задача решается методами корреляционного
и регрессионного анализа.
.
Эта задача решается методами корреляционного
и регрессионного анализа.
По сгущениям точек (рис.3) можно найти определенную зависимость, т.е. получить вид уравнения регрессии.
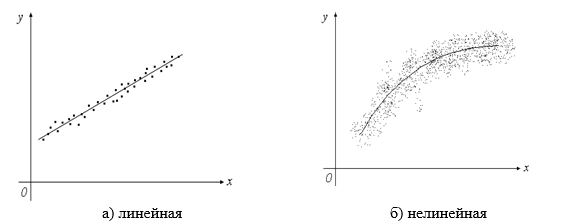 Рис.3.
Виды регрессии
Рис.3.
Виды регрессии
Если разброс точек значительный, то регрессии не будет. Следовательно, методы корреляционного и регрессионного анализа тесно связаны между собой.
Вид уравнения регрессии зависит от выбираемого метода приближения. Обычно используется метод наименьших квадратов.
|
|
где
 экспериментальные
и расчетные значения выходного параметра,
соответственно.
экспериментальные
и расчетные значения выходного параметра,
соответственно.
Рассмотрим различные случаи приближенной регрессии.
Линейная статистическая модель
(линейная регрессия от одного параметра)
При моделировании химико – технологических процессов (ХТП) во многих случаях связь между входными (x) и выходными (y) параметрами можно аппроксимировать линейным полиномом (зависимостью).

Для получения вида математической модели необходимо определить коэффициенты уравнения регрессии b0 и b1. Для этого применяется метод наименьших квадратов.

Таким образом, процедура нахождения коэффициентов регрессии сводится к задаче определения минимума функции. Необходимое условие минимума функции является равенство нулю частных производных функции по исходным величинам (коэффициентам).



Решая систему уравнений, выражаем коэффициенты b0 и b1.


После вычисления коэффициентов необходимо провести статистический анализ полученного уравнения регрессии с целью проверки модели на адекватность.
Статистические модели в виде нелинейных полиномов.
Параболическая регрессия.
При составлении статистических моделей ХТП часто возникает необходимость использовать уравнения нелинейной формы, в частности полином второй степени.

Коэффициенты регрессии определяем по методу наименьших квадратов.

Приравняем к нулю частные производные функции по коэффициентам b0, b1, b2.

Выполнив преобразования, получим систему линейных уравнений с тремя неизвестными (b0, b1,b2).

Введем обозначения.
для расчета коэффициентов регрессии:
 ;
;  ;
;  ;
;  ;
;
(18)
 ;
;  ;
;  .
.
– для
расчета коэффициента корреляции:

С учетом принятых обозначений система будет иметь следующий вид:

Определим неизвестные коэффициенты b0, b1, b2.



После решения системы уравнений и вычисления коэффициентов b0, b1, b2 проводится статистический анализ полученного уравнения регрессии. Аналогичным образом будут определяться коэффициенты параболы любого порядка. Исследование уравнения проводится по статистическим критериям. Однако в этом случае не требуется вычислять выборочные коэффициенты корреляции. Адекватности уравнения регрессии эксперименту можно добиться, повышая степень полинома. Однако при этом все коэффициенты следует вычислять заново, так как существует корреляция между коэффициентами.




 или
или