
Готовые РГР / Расчетно-графическая работа Вариант 0
.pdfМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение высшего образования «Казанский национальный исследовательский технический университет им. А.Н.
Туполева-КАИ» (КНИТУ-КАИ)
ИНСТИТУТ РАДИОЭЛЕКТРОНИКИ И ТЕЛЕКОММУНИКАЦИЙ
(наименование института (факультета), филиала)
Кафедра Радиофотоники и микроволновых технологий (РФМТ)
11.03.01 «Радиотехника»
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА ПО ДИСЦИПЛИНЕ
Цифровая обработка сигналов
|
Вариант 0 |
|
||
Студент Смирнов Н.Ю. |
|
5471 |
|
_______________ |
(Ф.И.О.) |
(номер группы) |
(подпись, дата) |
||
Руководитель к.т.н, доцент каф. РФМТ |
Аглиуллин А.Ф. |
|||
(должность) |
|
|
|
(Ф.И.О.) |
Казань, 2020 г.
|
Содержание |
Задание №1.................................................................................................................................. |
3 |
Решение ....................................................................................................................................... |
4 |
Задание №2.................................................................................................................................. |
9 |
Решение: ...................................................................................................................................... |
9 |
Задание №3................................................................................................................................ |
11 |
Решение: .................................................................................................................................... |
12 |
Приложения. ............................................................................................................................. |
21 |
2

Задание №1.
Моделирование процесса дискретизации аналогового сигнала и восстановления аналогового сигнала из дискретного.
Наблюдение эффектов размножения и наложения спектров Требуется:
1.Сформировать аналоговый сигнал x(t) в виде суммы трех гармонических колебаний
x(t) x1 (t) x2 (t) x3 (t), |
(1) |
где
x1 (t) X1 cos(2 F1t 1 ), x2 (t) X2 cos(2 F2 t 2 ), x3 (t) X3 cos(2 F3t 3 ),
F2 =2 F1, F3 = 3 F1.
При моделировании аналогового сигнала на ЭВМ следует принять t it,
где t - временной интервал между двумя соседними расчетными точками, i – порядковый номер расчетной точки, изменяющийся от 0 до imax.
Значения X1, X2, X3, φ1, φ2, φ3, F1 и t приведены в таблице 1.
Таблица 1. Исходные данные для выполнения задания №1
Номер варианта- |
|
|
|
|
|
|
|
|
|
|
-последняя цифра |
X1 |
X2 |
X3 |
φ1 |
φ 2 |
φ 3 |
F1 |
FД |
Δt |
|
номера |
||||||||||
|
|
|
|
|
|
|
|
|
||
студенческого |
|
|
|
|
|
|
|
|
|
|
билета |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0.5 |
0 |
0 |
0 |
1кГц |
8кГц |
1/512 мс |
|
|
|
|
|
|
|
|
|
|
|
2.Определить амплитудный спектр аналогового сигнала.
3.Сформировать вспомогательный сигнал u(t) в виде периодической последователь-
ности единичных отсчетов с периодом, равным интервалу дискретизации TД 1 , где
FД
FД – частота дискретизации (рисунок 1). Значение FД приведено в таблице 1.
u(t) |
|
|
|
|
|
|
|
TД |
|||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рисунок 1 – Вспомогательный сигнал в виде последовательности единичных отсчетов
4. Сформировать дискретный сигнал xd (t) x(t) u(t) .
5.Определить амплитудные спектры аналогового и дискретного сигналов и убедиться
втом, что при дискретизации имеет место эффект размножения спектра аналогового сигнала.
6.Восстановить аналоговый сигнал из дискретного путем выделения из спектра дискретного сигнала той части, которая соответствует спектру аналогового сигнала. Сравнить восстановленный сигнал с исходным аналоговым сигналом.
3

7. Повторить машинный эксперимент при в два раза меньшей частоте дискретизации. Убедиться в том, что восстановленный сигнал отличается от исходного аналогового сигнала, и объяснить причину искажения восстановленного сигнала.
Решение
Для моделирования аналогового сигнала преобразуем соотношение (1), определив количество расчетных точек is в периоде T1 аналогового сигнала
is T1 1 ,
t F1 t
Сучетом последнего соотношения сигнал в расчетной точке i определяется следую-
щим образом:
x(i) x1(i) x2 (i) x3 (i), |
(2) |
где
|
|
|
|
|
1 10 3 10 3 |
|
|
|
|
|
1cos 1,953 10 3 |
||||||
x |
|
i 1cos 2 i |
|
|
|
|
|
|
0 |
|
|||||||
|
|
|
|
|
|
||||||||||||
1 |
|
|
|
|
|
512 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 10 3 10 3 |
|
|
|
|
|
|
|||||
x |
2 |
i 0 cos |
2 i |
|
|
|
|
|
0 |
|
0 |
||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
512 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 10 3 |
10 |
3 |
|
|
|
|
|
0,5 cos 11,72 |
||
x |
3 |
i 0,5cos |
2 i |
|
|
|
|
|
|
|
0 |
|
|||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
512 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x i cos 1,953 10 3 i 0,5 cos 11,72 10 3 i
i ,
10 3 i
|
Количество |
расчетных |
точек |
|
|
в |
|
|
интервале |
|
|
дискретизации |
равно |
||||||||||||||||||||
id |
|
|
1 |
|
|
512 |
64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
F |
t |
8 103 10 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поэтому вместо функции u t |
можно рассматривать функцию u i , график которой |
|||||||||||||||||||||||||||||||
приведен на рисунке 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
u(i) |
|
|
|
|
|
id |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Сигнал u i |
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 2 |
|
|
|
|
|||||||||||||||
|
формируется в цикле по порядковому номеру расчетной точки i |
с ис- |
|||||||||||||||||||||||||||||||
пользованием счетчика расчетных точек, переменная которого z изменяется от нуля до id. Алгоритм формирования i – го значения сигнала u i приведен на рисунке 3
4
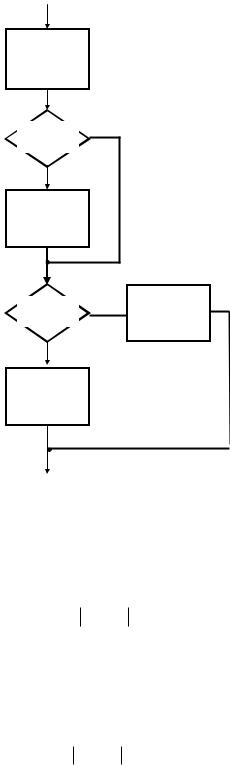
z=z+1 |
|
|
|
нет |
|
z=id? |
|
|
да |
|
|
z=0 |
|
|
|
нет |
u(i)=0 |
z=0? |
|
|
|
|
|
да |
|
|
u(i)=1 |
|
|
Рисунок 3 – Алгоритм формирования вспомогательного сигнала
Дискретный сигнал определяется следующим соотношением |
|
x Д i x i u i . |
(3) |
Рассчитаем частоты спектральных составляющих дискретного сигнала, учитывая, что размножение спектра осуществляется по закону:
kFd F ,
где F – частота спектральной составляющей аналогового сигнала, k = 0, 1, 2, 3. . .
В рассматриваемом случае частота F принимает значения F1, F2 и F3.
Расчет нужно выполнить при k = 0 и k = 1, а рассчитанные частоты представить в порядке возрастания.
Расчет частот спектральных составляющих дискретного сигнала по формуле
kFd F
k = 0
F=F1, f1 = F1 = 1 кГц, F=F2, f2 = F2 = 2 кГц, F=F3, f3 = F3 = 3 кГц. K=1
F=F3, f4 = Fd – F3 = 8 – 3 = 5 кГц, F=F2, f5 = Fd – F2 = 8 – 2 = 6 кГц, F=F1, f6 = Fd – F1 = 8 – 1 = 7 кГц, F=F1, f7 = Fd + F1 = 8 + 1 = 9 кГц, F=F2, f8 = Fd + F2 = 8 + 2 = 10 кГц, F=F3, f9 = Fd + F3 = 8 + 3 = 11 кГц.
5
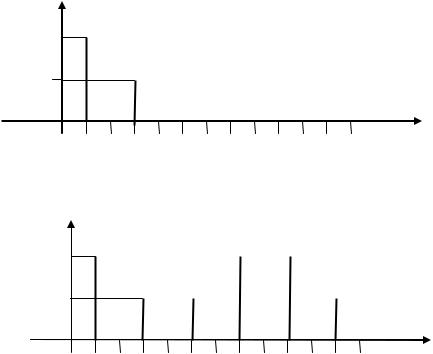
Построение спектральных диаграмм аналогового и дискретного сигналов
X
1
0,5
0 1 2 3 4 5 6 7 8 9 10 11 12 |
f кГц |
Рисунок 4 – Амплитудный спектр аналогового сигнала
X/Xmax
1
0,5
0 1 2 3 4 5 6 7 8 9 10 11 12 |
f кГц |
Рисунок 5 – Амплитудный спектр дискретного сигнала
На рисунке 5 амплитудный спектр представлен в относительном масштабе по оси ординат как отношение амплитуды спектральной составляющей X к максимальной амплитуде Xmax.
1.Результат моделирования по программе «Diskret» при исходных данных таблицы 1 в виде временных и спектральных диаграмм аналогового и дискретного сигнала приведён на рисунке 6
6
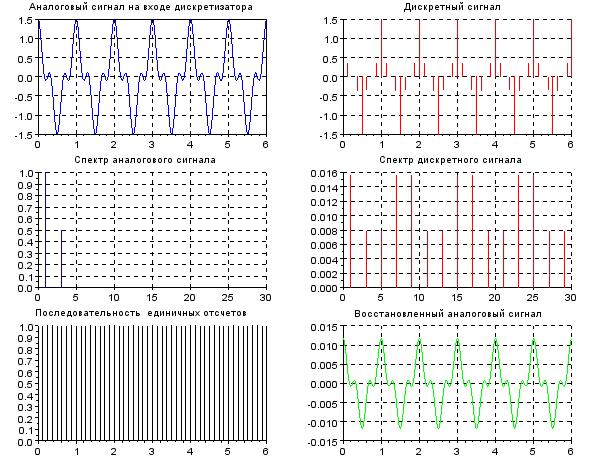
Рисунок 6. Временные и спектральные диаграммы при FД > 2F3
Проанализируем полученные временные и спектральные диаграммы:
Сравнивая спектры аналогового и дискретного сигналов, можно сделать вывод о том, что спектр дискретного сигнала представляет собой сумму бесконечно большого числа «копий» спектра аналогового сигнала, расположенных на оси частот
через одинаковые интервалы.
Иначе говоря: спектр дискретного сигнала состоит из суммы спектров исходного непрерывного сигнала, сдвинутых друг относительно друга по оси частот на величину равную частоте дискретизации FД.
Спектры аналогового и дискретного сигналов совпадают в диапазоне частот
[-0,5 FД ; 0,5 FД]
Аналоговый сигнал, восстановленный из дискретного идентичен по форме исходному аналоговому сигналу, действующему на входе дискретизатора, но меньше по амплитуде.
Выводы:
Сгустки спектра дискретного сигнала соответствуют спектру соответствующего аналогового сигнала.
Восстановленный сигнал полностью идентичен по форме исходному аналоговому и меньше по амплитуде.
Несоответствие восстановленного сигнала исходному аналоговому сигналу по амплитуде обусловлено.
Повторим эксперимент при в два раза меньшей частоте дискретизации. Результат моделирования в виде временных и спектральных диаграмм аналогового и дискретного сигнала приведён на рисунке 7.
7
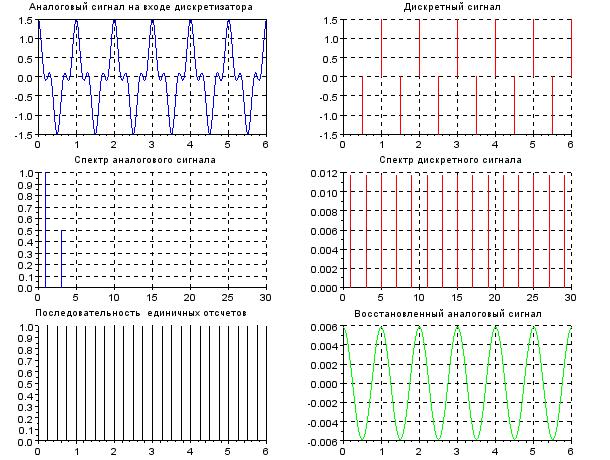
Рисунок 7. Временные и спектральные диаграммы при FД < 2F3
Выводы:
если условие FД > 2F3 не выполняется (Рис 7), смежные спектры частично перекрываются. В этом случае сгустки спектра распределяются по оси частот неравномерно, в результате чего возникает наложение спектров, приводящее к искажению сигнала. Эти искажения являются неустранимыми и называются ошибками наложения.
Сигнал восстанавливается без искажений, если выполняется условие (FД > 2F3), в противном случае сигнал восстанавливается с искажениями, обусловленными ошибками наложения, что и доказывается при сравнении исходного аналогового сигнала и восстановленного аналогового сигнала.
Заключение:
При дискретизации аналогового сигнала возникают два эффекта, касающиеся спектра сигнала:
1.Эффект размножения спектра аналогового сигнала,
2.Эффект наложения сгустков спектра дискретного сигнала друг на друга.
Эффект наложения спектров приводит к искажению дискретного сигнала и невозможности точного восстановления аналогового сигнала из дискретного.
Спектр дискретного сигнала представляет собой периодическую функцию частоты, период которой равен частоте дискретизации.
Если дискретизации подвергается периодический аналоговый сигнал с линейчатым спектром, то размножение спектра осуществляется по закону:
kFд F при k=0,1,..K
где F – частота спектральной составляющей аналогового сигнала.
Амплитуды спектральных составляющих дискретного сигнала пропорциональны соответствующим составляющим спектра аналогового сигнала.
8
Размножение спектра апериодического аналогового сигнала осуществляется по этому же закону, если рассматривать в качестве F характерные частоты непрерывного спектра аналогового сигнала.
Эффект наложения спектров при дискретизации отсутствует, если выполняется условие Fд >2Fmax.
Задание №2.
Определение системной функции, комплексного коэффициента передачи, АЧХ и ФЧХ цифрового фильтра
Требуется определить системную функцию H(z), комплексный коэффициент передачи K(jθ), АЧХ K(fN) и ФЧХ φ(fN) цифрового фильтра, где θ = 2π fN, fN=f/FД – нормированная частота.
Построить графики АЧХ и ФЧХ В таблице 2 приведены номер рисунка с графическим изображением алгоритма функ-
ционирования цифрового фильтра и коэффициенты системной функции фильтра. Номер варианта – последняя цифра номера студенческого билета.
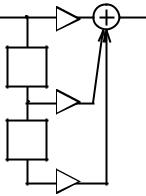
Таблица 2. Алгоритм функционирования и параметры цифрового фильтра
Номер |
Номер |
|
варианта |
рисунка |
Коэффициенты системной функции фильтра |
|
|
|
0 |
8 |
B0 = B2 = 0.65, B1 = 1 |
|
|
|
x n |
B 0 |
yn |
|
||
|
Z -1 |
|
|
B 1 |
|
|
Z -1 |
|
|
B 2 |
|
Рисунок 8 (рисунок 8 МУ) Графическое представление алгоритма функционирования фильтра
Решение:
Определим системную функцию H(z), комплексный коэффициент передачи K(jθ), АЧХ K(fN) и ФЧХ φ(fN) цифрового фильтра, где θ = 2π fN, fN=f/FД - нормированная частота.
Из рисунка видно, что
yn B0 xn B1 xn 1 B2 xn 2
2. Воспользовавшись свойствами Z-преобразования, перейдем от разностных уравнений к уравнениям для Z-преобразований дискретных сигналов xn, yn
Y (z) B0 X (z) B1 z 1 X (z) B2 z 2 X (z)
Разделив Y(z) на X(z), получим системную функцию цифрового фильтра:
Н (z) |
Y (z) |
|
B X (z) B z 1 X (z) B z 2 X (z) |
B |
B z 1 |
B z 2 |
||
|
0 |
1 |
2 |
|||||
|
|
|
|
|||||
|
X (z) |
|
|
|
X (z) |
0 |
1 |
2 |
|
|
|
|
|
|
|
||
Определим комплексный коэффициент передачи, используя подстановку z e j
9
K ( j ) B0 B1e j B2 e j 2 B0 B1 ((cos( ) j sin( )) B2 ((cos(2 ) j sin( 2 ))B0 B1 (cos( ) B2 ((cos(2 ) j(B1 sin( ) B2 sin( 2 ))
Найдем АЧХ линии задержки:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K ( ) |
|
K ( j ) |
|
|
|
(B B (cos( ) B |
((cos(2 ))2 |
(B sin( ) B |
2 |
sin( 2 ))2 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
(B |
B (cos( ) B |
((cos(2 ))2 (B sin( ) B |
2 |
sin( 2 ))2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
0 |
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
B 2 |
B 2 |
B |
2 2B (B |
0 |
B |
) cos( ) B |
2 |
cos(2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
0 |
|
|
|
1 |
2 |
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
или K ( f |
N |
) |
|
K ( j2f |
N |
) |
|
|
|
B 2 B 2 |
B 2 |
2B (B |
B |
) cos(2f |
N |
) B |
2 |
cos(4f |
N |
) |
|||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
2 |
|
|
1 |
|
0 |
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
1,845 2,6 cos(2f N ) 0,65 cos(4f N ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
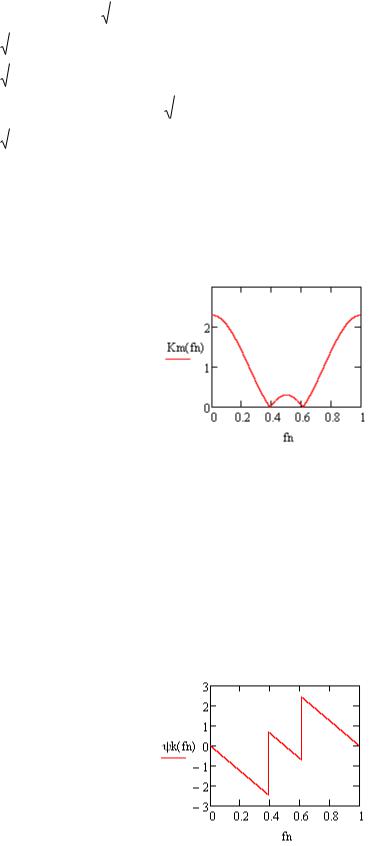
Построим график АЧХ (рисунок 9) при изменении fN от 0 до 1 с шагом 0.0001. Приня-
тый интервал изменения fN соответствует интервалу частот от 0 до FД 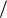 2 . Внутри этого
2 . Внутри этого
интервала (кроме частоты FД  2 ) выполняется теорема Котельникова.
2 ) выполняется теорема Котельникова.
Из графика АЧХ следует, что данный фильтр является режекторным. Его коэффициент передачи равен 2,25 при fN =0 и fN =1, равен 0 при fN =0,4 и fN =0,6, т.е. на частоте, равной 0,4 и 0,6 частоты дискретизации.
Рисунок 9 - АЧХ фильтра
Определим ФЧХ фильтра Из выражения для комплексного коэффициента передачи следует, что его аргумент
равен |
|
|
|
|
|
|
|
arg(K( j )). |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
B sin( ) B |
2 |
sin( 2 ) |
|
|
|
B |
0 |
sin( ) B |
2 |
sin( 2 ) |
|
|||||
arctg |
|
|
|
1 |
|
|
|
|
arctg |
|
|
|
|
|
|
|
или |
|||
|
|
B (cos( ) B |
|
|
|
|
B (cos( ) B |
|
|
|||||||||||
|
|
B |
0 |
2 |
((cos(2 ) |
B |
0 |
2 |
((cos(2 ) |
|||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
B0 sin( 2 f N ) B2 |
sin( 4 f N ) |
|
|
|
|
||||
f N |
arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B (cos(2 f |
|
) B |
|
((cos(4 |
f |
|
|
||||
|
B |
0 |
N |
2 |
N |
) |
|||||||
|
|
|
1 |
|
|
|
|
|
|
||||
График f N |
приведен на рисунке 10. |
|
|
|
|
||||||||
Рисунок 10 – ФЧХ фильтра
10
